Краткая информация
Определяет, проявляют ли пространственные объекты, или ассоциированные с ними значения, статистически значимую кластеризацию или дисперсию по диапазону расстояний.
Иллюстрация
Использование
Для точного измерения расстояний этому инструменту требуются проецированные данные.
Выходные данные инструмента – это таблица с полями: ExpectedK и ObservedK, соответственно содержащие ожидаемые и наблюдаемые значения К-функции. Так как применяется преобразование L(d), значения ExpectedK всегда будут совпадать со значением расстояния. Поле DiffK содержит разность между наблюдаемыми и ожидаемыми значениями К-функции. Если включена функция расчета доверительного интервала, два дополнительных поля, LwConfEnv и HiConfEnv также будут включены в итоговую таблицу. Эти поля содержат информацию о доверительных интервалах для каждой итерации, заданных параметром Число диапазонов расстояний. Инструмент К-функция дополнительно может создать графический слой, иллюстрирующий полученные результаты.
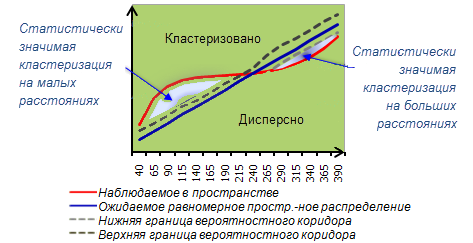
Когда наблюдаемые значения К больше, чем ожидаемые значения К для определенного расстояния, в таком случае распределение более кластеризовано нежели случайно для обозначенного расстояния (масштаб анализа). Когда наблюдаемые значения К меньше, чем ожидаемые значения К, распределение более дисперсно нежели случайно для обозначенного расстояния (масштаб анализа). Когда наблюдаемые значения К больше, чем HiConfEnv, пространственную кластеризацию для данного расстояния можно считать статистически значимой. Когда наблюдаемые значения К меньше, чем значение LwConfEnv, пространственную дисперсию для данного расстояния можно считать статистически значимой. Дополнительную информацию см. в разделе Как работает пространственный кластерный анализ на основе множественных расстояний (Функция Ripley K) .
Включите параметр Отобразить результат графически для создания линейного графика, иллюстрирующего полученные результаты. Ожидаемые результаты будут представлены в виде голубой линии, в то время как наблюдаемые – красной линией. Отклонение линии с наблюдаемыми результатами над линией с ожидаемыми результатами свидетельствует о том, что существует кластеризация для данного расстояния. Отклонение линии с наблюдаемыми результатами под линией с ожидаемыми результатами свидетельствует о том, что существует дисперсия для данного расстояния. Линейный график создается как графический слой; графические слои временные и будут удалены по мере закрытия приложения ArcMap. Щелкните правой кнопкой мыши графический слой и выберите Сохранить, чтобы записать диаграмму в файл графики. Если вы сохраните ваш проект с картой после сохранения графика, связь с графическим файлом будет сохранена в проекте .mxd. Более подробно о файлах графики см. в разделе Изучение и визуализация данных при помощи графиков (диаграмм).
-
Для линейных или полигональных объектов, при расчете расстояний используются центроиды. Для мультиточек, полилиний или полигонов, состоящих их нескольких частей, центроид вычисляется с использованием средневзвешенного центра всех частей объекта. При определении весов точечные объекты имеют равный вес (1). Для линейных объектов это длина сегмента. Для полигональных – площадь.
Поле веса используется наиболее подходящим образом, когда отражает количество случаев или вычисления.
Когда Поле веса не определено, наибольшее значение Разница К соответствует расстоянию, на котором пространственные процессы кластеризуются в более явной форме.
Ниже объясняется, как производится расчет доверительных границ:
- Без Поля веса
Когда Поле веса не определено, доверительная граница конструируется посредством случайного распределения точек в пределах изучаемой области и для данного распределения вычисляется значение L(d). Каждое случайное перераспределение точек носит название "перестановка". Если, например, выбрано 99_PERMUTATIONS инструмент случайным выбором перераспределит набор исходных точек 99 раз для каждой итерации. После распределения набора точек 99 раз инструмент выберет для каждого расстояния два Наблюдаемые значения К, максимально отклоняющиеся от Ожидаемого К (сверху и снизу); эти значения сформируют доверительный интервал.
- С Полем веса
Когда Поле веса определено, только значения весов случайным образом перераспределяются, чтобы рассчитать доверительные границы, в то время как местоположение точек остается фиксированным. По существу, когда Поле веса определено, местоположение остается фиксированным и инструмент оценивает кластеризацию значений объектов в пространстве. С другой стороны, когда Поле веса определено, инструмент анализирует кластеризацию/дисперсию положения объектов.
- Без Поля веса
Поскольку доверительные границы определяются исходя из случайных перестановок, значения, определяющие доверительные границы, будут изменяться с каждым запуском инструмента, даже если входные параметры идентичны. Однако если вы установите начальное значение для генератора случайных чисел, повторяющийся анализ даст стабильные результаты.
Несколько перестановок, выбранных для параметра Вычисление доверительные границы, могут быть свободно соотнесены с доверительными уровнями: 9 для 90%, 99 для 99%, и 999 для 99,9%.
Когда изучаемая область не указана, инструмент использует минимальный прямоугольник, включающий в себя все точки, в качестве полигональной области изучения. В отличие от экстента минимальный описывающий прямоугольник может не совпадать с осями Х и У.
К-функция очень чувствительна к размеру области изучения. Идентично расположенные точки могут быть кластеризованы или распределены дисперсно в зависимости от размера окружающей их области исследования. Поэтому необходимо особенно тщательно подходить к выбору границ области изучения. Приведенный ниже рисунок демонстрирует классический пример, как идентично расположенные объекты могут кластеризоваться или располагаться рассеянно в зависимости от указанной области изучения.
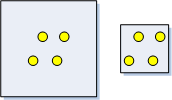
Класс объектов для области изучения необходим, если USER_PROVIDED_STUDY_AREA_FEATURE_CLASS выбрано для параметра Метод изучаемой области.
Если Класс объектов изучаемой территории задан, он должен строго содержать только 1 объект (полигон области изучения).
Если Начальное расстояние или Приращение расстояния не определены, тогда значения по умолчанию рассчитываются с учетом экстента Входного класса объектов.
K-функция не учитывает полностью отклонения для объектов, расположенных около границы области исследования. Метод коррекции границ предусматривает подходы для реагирования на эти отклонения.
- NONE
Никакой специальной коррекции границ не применено. Однако точки, входящие во Входной класс объектов и располагающиеся за пределами области изучения, определенной пользователем, используются в соседних вычислениях. Этот метод подходит, если вы собрали данные с очень большой области изучения, но нуждаетесь в анализе меньших областей, попадающих внутрь границ, отделяющих собранные вами данные.
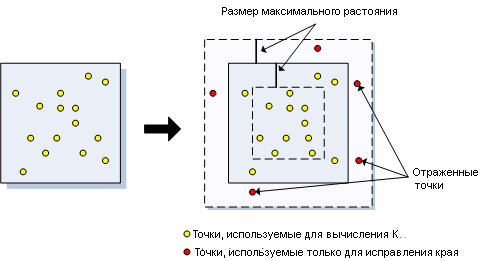
- SIMULATE_OUTER_BOUNDARY_VALUES
Этот метод создает точки за пределами границ области изучения, которые отражают точки, найденные внутри области исследования, чтобы исправить недооценку рядом с границами. Точки, располагающиеся в пределах расстояния, равного максимальному диапазону расстояний от границы области изучения, отражаются. Отраженные точки используются с тем расчетом, чтобы приграничные точки могли иметь более точные оценки. Представленная снизу диаграмма иллюстрирует, какие точки будут использованы в расчетах и какие будут только использоваться для корректировки приграничных.
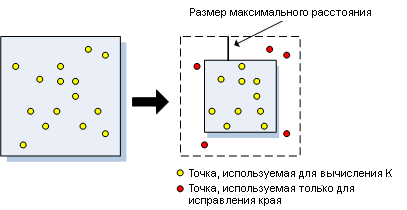
- REDUCE_ANALYSIS_AREA
Данная методика корректировки сужает размер области анализа на расстояние, равное наибольшему диапазону расстояний, используемому в анализе. После сужения области изучения, точки, находящиеся за пределами новой области исследования, будут рассматриваться только тогда, когда соседние вычисления оцениваются для точек, все еще располагающихся внутри области изучения. Ни в каком другом виде они не будут использоваться при вычислении К-функции. Представленная снизу диаграмма иллюстрирует, какие точки будут использованы в расчетах и какие будут только использоваться для корректировки приграничных.
- RIPLEY'S_EDGE_CORRECTION_FORMULA
Этот метод анализирует расстояние от каждой точки до границ области изучения и до каждого ее соседа. Всем соседям, которые удалены от точки интереса на расстояние большее, нежели расстояние от точки до границы области изучения, приписываются дополнительные веса. Этот метод корректировки ребер подходит только для изучаемых областей, имеющих квадратную или прямоугольную форму, или когда вы выбираете значение MINIMUM_ENCLOSING_RECTANGLE для параметра Метод изучаемой области.
- NONE
Если метод коррекции границ не применяется, смещение увеличивается при увеличении расстояния. Если включить параметр Отобразить результат графически, то вы заметите, что линия ObservedK свисает на более дальних расстояниях.
С математической точки зрения Многовариантный пространственный кластерный анализ (Функция Ripley's K) использует обычную трансформацию К-функции Рипли, где ожидаемые результаты по случайному набору точек соответствуют входному расстоянию. Преобразование L(d) показано ниже.
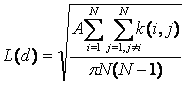
где А – область, N – количество точек, d – расстояние и k(i, j) – вес, который (если нет приграничных исправлений) равен 1, когда расстояние между i и j меньше или рано d и равен нулю, когда расстояние между i и j больше d. Когда приграничная корректировка применяется, веса k(i,j) слегка изменяются.
-
Слои карты можно использовать для определения Входного класса объектов. Если в слое есть выборка, только выбранные объекты будут включены в анализ.
Синтаксис
MultiDistanceSpatialClustering_stats (Input_Feature_Class, Output_Table, Number_of_Distance_Bands, {Compute_Confidence_Envelope}, {Display_Results_Graphically}, {Weight_Field}, {Beginning_Distance}, {Distance_Increment}, {Boundary_Correction_Method}, {Study_Area_Method}, {Study_Area_Feature_Class})| Параметр | Объяснение | Тип данных |
Input_Feature_Class | Класс объектов, по которому будет выполняться анализ. | Feature Layer |
Output_Table | Таблица, в которую будут записаны результаты анализа | Table |
Number_of_Distance_Bands | Количество раз, чтобы увеличить размер соседства и проанализировать набор данных для выявления кластеризации. Начальная точка и размер приращения указываются в параметрах Beginning_Distance и Distance_Increment соответственно. | Long |
Compute_Confidence_Envelope (Дополнительный) | Доверительные границы рассчитываются путем случайного перераспределения точечных объектов (или их значений) по области изучения. Количество точек/значений, перераспределенных случайным образом, соответствует количеству точек, содержащихся в классе объектов. Каждая очередь случайных перераспределений называется "перестановка", и доверительные границы создаются на основе этих перестановок. Этот параметр позволяет вам выбрать, сколько перестановок следует использовать для расчета доверительных границ.
| String |
Display_Results_Graphically (Дополнительный) | Указывает, будет ли инструмент создавать графический слой, обобщающий результаты.
| Boolean |
Weight_Field (Дополнительный) | Числовое поле веса, отражающее количество объектов/событий в каждом местоположении. | Field |
Beginning_Distance (Дополнительный) | Расстояние, на котором необходимо начать кластерный анализ и расстояние, от которого необходимо начать приращение. Введенное значение параметра должно быть в таких же единицах, что и Выходная система координат. | Double |
Distance_Increment (Дополнительный) | Расстояние, на которое необходимо увеличивать при каждой последующей итерации. Расстояние, используемое в этом анализе, начинается от Beginning_Distance и увеличивается на величину, указанную в Distance_Increment. Значение этого параметра должно измеряться в единицах параметра среды Выходная система координат. | Double |
Boundary_Correction_Method (Дополнительный) | Данный метод используется для корректировки недооценок количества соседей для объектов, расположенных рядом с границами области изучения.
| String |
Study_Area_Method (Дополнительный) | Указывает регион, который необходимо использовать для области изучения. К-функция чувствительна к изменениям в размере области изучения, в связи с чем необходим тщательный выбор значения.
| String |
Study_Area_Feature_Class (Дополнительный) | Класс объектов, который очерчивает область, по которой следует анализировать входной класс объектов. Указан, только если Study_Area_Method = "USER_PROVIDED_STUDY_AREA_FEATURE_CLASS" . | Feature Layer |
Производные выходные данные
| Name | Объяснение | Тип данных |
| Result_Image |
Пример кода
Multi-DistanceSpatialClusterAnalysis, пример 1 (окно Python)
Следующий скрипт, представленный в окне Python, демонстрирует, как использовать инструмент Multi-DistanceSpatialClusterAnalysis.
import arcpy
arcpy.env.workspace = r"C:\data"
arcpy.MultiDistanceSpatialClustering_stats("911Calls.shp","kFunResult.dbf", 11,
"0_PERMUTATIONS_-_NO_CONFIDENCE_ENVELOPE",
"NO_DISPLAY", "#", 1000, 200,"REDUCE_ANALYSIS_AREA",
"MINIMUM_ENCLOSING_RECTANGLE", "#")
Multi-DistanceSpatialClusterAnalysis, пример 2 (автономный скрипт Python)
Следующий автономный скрипт Python демонстрирует, как использовать инструмент Multi-DistanceSpatialClusterAnalysis.
# Use Ripley's K-Function to analyze the spatial distribution of 911
# calls in Portland Oregon
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\Data"
try:
# Set the current workspace (to avoid having to specify the full path to the feature classes each time)
arcpy.env.workspace = workspace
# Set Distance Band Parameters: Analyze clustering of 911 calls from
# 1000 to 3000 feet by 200 foot increments
numDistances = 11
startDistance = 1000.0
increment = 200.0
# Process: Run K-Function...
kFun = arcpy.MultiDistanceSpatialClustering_stats("911Calls.shp",
"kFunResult.dbf", numDistances,
"0_PERMUTATIONS_-_NO_CONFIDENCE_ENVELOPE",
"NO_DISPLAY", "#", startDistance, increment,
"REDUCE_ANALYSIS_AREA",
"MINIMUM_ENCLOSING_RECTANGLE", "#")
except:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())
Параметры среды
Информация о лицензиях
- ArcGIS Desktop Basic: Да
- ArcGIS Desktop Standard: Да
- ArcGIS Desktop Advanced: Да
Связанные разделы
- Обзор группы инструментов Анализ структурных закономерностей
- Моделирование пространственных отношений
- Что такое z-оценка? Что такое p-значение?
- Среднее Ближайшее соседство
- Пространственная автокорреляция (Глобальный индекс Морана I)
- Как работает пространственный кластерный анализ на основе множественных расстояний (К-функция Рипли)