ArcMap

Пространственная автокорреляция (Глобальный индекс Морана I)

Краткая информация

Измеряет пространственную автокорреляцию на основе местоположений пространственных объектов и атрибутивных значений, используя статистику общего индекса I Морана.

Доступ к результатам этого инструмента (в том числе дополнительному PDF-файлу отчета) можно получить в окне Результаты. Если отключить фоновую обработку, результаты также будут показаны в диалоговом окне Ход процесса.

Более подробно о том, как работает Пространственная автокорреляция (Глобальный индекс Морана I)

Иллюстрация

Иллюстрация вычисления Глобального индекса Морана

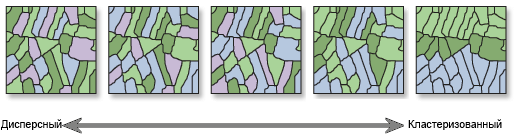
Использование

  • Инструмент Пространственная автокорреляция возвращает пять значений: Индекс I Морана, Ожидаемый индекс, Дисперсия, z-оценка и p-значение. Эти значения доступны в окне результатов и также передаются в качестве производных выходных данных для потенциального использования в моделях и скриптах. Дополнительно, этот инструмент создаст HTML-файл с графическим представлением результатов. Если дважды щелкнуть HTML-файл в окне результатов, данный HTML-файл откроется в установленном по умолчанию браузере. Если щелкнуть правой кнопкой мыши запись Сообщения в окне Результаты и выбрать Вид, результаты можно будет просмотреть в диалоговом окне Сообщение. Если инструмент будет работать в фоновом режиме, выходные значения также будут показаны в диалоговом окне работы инструмента.

    Результаты работы инструмента отображаются в окне результатов.

  • Исходя из предложенного набора объектов и связанных с ними атрибутов, этот инструмент оценивает, является ли модель сгруппированной (кластерной), рассредоточенной (дисперсионной) или случайной. Когда z-оценка или p-значение указывают на статистическую значимость, положительный индекс Морана I свидетельствует о тенденции к кластеризации, в то время как отрицательные значения индекса Морана говорят о тенденции к дисперсному распределению объектов (явлений).

  • Этот инструмент вычисляет z-оценку и p-значение, по которым принимается решение об отклонении нулевой гипотезы. В этом случае нулевая гипотеза утверждает, что объекты случайно распределены по области изучения.
  • Z-оценки и р-значения являются измерителями статистической значимости, которая свидетельствует о возможности отклонить нулевую гипотезу. Для этого инструмента нулевая гипотеза утверждает, что значения, связанные с объектами, распределены хаотично.

  • Входное поле должно содержать разные значения. Для математических расчетов, выполняемых в рамках этих статистических операций, требуется, чтобы исходные переменные были разными. Например, анализ не будет выполняться, если все входящие значения равны 1. Если вы хотите использовать данный инструмент для анализа пространственных закономерностей случайных данных, попробуйте агрегировать ваши случайные данные. Для анализа пространственных закономерностей случайных данных может также использоваться инструмент Оптимизированный анализ горячих точек.

  • Когда Входной класс объектов не имеет проекции (т.е. когда координаты заданы в градусах, минутах и секундах), или когда в качестве выходной системы координат используется Географическая система координат, расстояния в этих случаях будут рассчитываться с помощью хордовых измерений. Измерения хордовых расстояний применяются постольку, поскольку они могут быть быстро вычислены и дают очень хорошие оценки истинных геодезических расстояний, по крайней мере, для точек, расстояние между которыми в пределах порядка тридцати градусов. Хордовые расстояния основаны на эллипсоиде вращения. Если взять две любые точки на поверхности Земли, то хордовым расстоянием между ними будет длина прямой линии, проходящей через трехмерное тело Земли и соединяющей эти две точки. Хордовые расстояния выражаются в метрах.

  • Когда при анализе используются хордовые расстояния, параметр Диапазон расстояний или пороговое расстояние, если он указывается, должен быть выражен в метрах.

  • В более ранних версиях, чем ArcGIS 10.2.1, вы бы увидели предупреждение о том, что выбранные вами параметры и системные настройки предполагают проведение вычислений на основе географических координат (градусы, минуты, секунды). Увидев это предупреждение, необходимо было произвести проецирование данных в Систему координат проекции для того, чтобы вычисление расстояний было точным. Однако, начиная с версии 10.2.1, этот инструмент рассчитывает хордовые расстояния для всех случаев, когда требуются вычисления в географической системе координат.

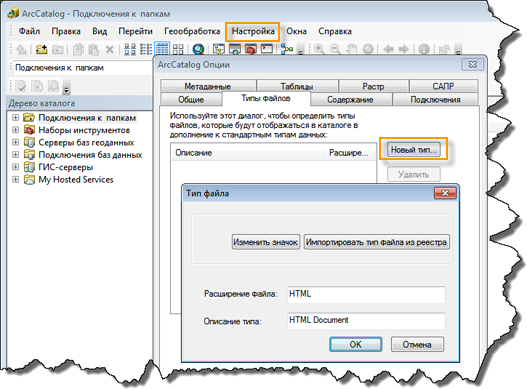
  • Этот инструмент при необходимости создает HTML-файл со сводным представлением результатов. HTML-файл не отображается автоматически в окне каталога. Если необходимо отобразить файлы HTML в Каталоге, выберите опцию меню Настроить, щелкнитеОпции ArcCatalog и выберите вкладку Типы файлов. Щелкните кнопку Новый тип и укажите HTML в качестве Расширения файла.

    Добавить файлы HTML в список файлов, который может быть показан в окне Каталога

  • Для линейных или полигональных объектов, при расчете расстояний используются центроиды. Для мультиточек, полилиний или полигонов, состоящих их нескольких частей, центроид вычисляется с использованием средневзвешенного центра всех частей объекта. При определении весов точечные объекты имеют равный вес (1). Для линейных объектов это длина сегмента. Для полигональных – площадь.

  • Выбор параметра Определение пространственных взаимоотношений должен отражать внутренние отношения между пространственными объектами, которые вы анализируете. Чем более точно вы сможете смоделировать взаимодействие пространственных объектов в пространстве, тем более точные результаты вы получите. Рекомендации см. в разделе Выбор Концептуализации пространственных отношений: рекомендации. Ниже приводится несколько дополнительных советов:

    • FIXED_DISTANCE_BAND

      Значение по умолчанию для параметра Диапазон расстояний или пороговое расстояние гарантирует, что каждый объект имеет, по крайней мере, одного соседа, и это важно. Но часто значение, заданное по умолчанию, не будет наиболее подходящим расстоянием для вашего анализа. В разделе Выбор фиксированного расстояния приведены стратегии, которые помогут определить значение диапазона расстояний, подходящее для вашего анализа.

    • INVERSE_DISTANCE или INVERSE_DISTANCE_SQUARED

      Когда для параметра Диапазон расстояний или пороговое расстояние указано значение 0, все объекты считаются соседями всех других объектов. Когда этот параметр остается пустым, применяется пороговое значение по умолчанию.

      Веса для расстояний менее 1 становятся не стабильны после обращения. Следовательно, при взвешивании для объектов, разделенных менее чем одной единицей расстояния, получают вес 1.

      При использовании опции обратного расстояния (INVERSE_DISTANCEINVERSE_DISTANCE_SQUARED или ZONE_OF_INDIFFERENCE) любым двум совпадающим точкам придается значение веса 1 во избежание деления на 0. Это будет гарантировать, что объекты не исключены из анализа.

  • Для параметра Определение пространственных взаимоотношений при использовании инструментов Построить матрицу пространственных весов или Построить матрицу пространственных весов для сети доступны дополнительные опции, в том числе пространственно-временные отношения. Чтобы эффективно применять дополнительные опции, с помощью одного из этих инструментов создайте файл матрицы пространственных весов до выполнения анализа, выберите значение GET_SPATIAL_WEIGHTS_FROM_FILE для параметра Определение пространственных взаимоотношений, а для параметра Файл матрицы весов укажите путь к файлу с пространственными весами, который вы создали.

  • Слои карты можно использовать для определения Входного класса объектов. Если в слое есть выборка, только выбранные объекты будут включены в анализ.

  • Если указан Файл матрицы весов с расширением .swm, инструмент предполагает получение файла матрицы весов, созданного , либо Построить матрицу пространственных весов или Построить матрицу пространственных весов для сети , иначе инструмент ожидает файл матрицы весов в формате ASCII. В некоторых случаях, поведение различно в зависимости от типа использованной матрицы весов:

    • ASCII-файлы с матрицей пространственных весов:
      • Веса используются без изменений. Отсутствующие отношения объект к объекту рассматриваются как нули.
      • Если веса нормализованы, то вероятнее всего, что результаты будут непригодны для анализа выбранного набора. Если вам нужно выполнить анализ выбранного набора данных, конвертируйте ASCII-файл с матрицей весов в SWM-файл, считав данные ASCII-файла в таблицу, затем используйте опцию CONVERT_TABLE с инструментом Построить матрицу пространственных весов.
    • Матрица пространственных весов в формате SWM:
      • Если веса уже были нормализованы, то они будут нормализованы вновь для выбранного набора данных. В противном случае они будут использоваться без изменений.

  • Для выполнения анализа с ASCII-файлом с матрицей пространственных весов требуется большой объем памяти. При анализе более 5000 объектов ASCII-файл с матрицей пространственных весов следует конвертировать в SWM-файл. Сначала вы вставляете ваш ASCII-файл с весами в форматированную таблицу (например, с помощью Excel). Затем запустите инструмент Построить матрицу пространственных весов с CONVERT_TABLE для параметра Определение пространственных взаимоотношений. В результате будет создан SWM-файл с матрицей пространственных весов.

  • Для полигональных объектов вы почти всегда будете выбиратьROW для параметра Стандартизация. Нормализация ряда нивелирует отклонение в ситуациях, когда количество соседей каждого объекта является функцией агрегирования или выборки, нежели отражением реального пространственного распределения анализируемой переменной.

  • Дополнительную информацию о параметрах инструмента см. в справочной статье Моделирование пространственных отношений.

Синтаксис

SpatialAutocorrelation_stats (Input_Feature_Class, Input_Field, {Generate_Report}, Conceptualization_of_Spatial_Relationships, Distance_Method, Standardization, {Distance_Band_or_Threshold_Distance}, {Weights_Matrix_File})
ПараметрОбъяснениеТип данных
Input_Feature_Class

Класс объектов, для которого будет рассчитываться пространственная автокорреляция.

Feature Layer
Input_Field

Числовое поле, используемое в оценке пространственной автокорреляции.

Field
Generate_Report
(Дополнительный)
  • NO_REPORT —Результаты не будут представлены в графической форме. Используется по умолчанию.
  • GENERATE_REPORT —Графическая сводка будет представлена в формате HTML-файла.
Boolean
Conceptualization_of_Spatial_Relationships

Определяет, как заданы пространственные отношения между объектами.

  • INVERSE_DISTANCE —Близко расположенные соседние объекты оказывают большее влияние на вычисления для целевого объекта, нежели удаленные объекты.
  • INVERSE_DISTANCE_SQUARED —То же самое, что и INVERSE_DISTANCE, только угол наклона острее, влияние объектов уменьшается быстрее, и лишь ближайшие соседи окажут существенное влияние на вычисления для рассматриваемого объекта.
  • FIXED_DISTANCE_BAND —Каждый объект анализируется в контексте соседних объектов. Соседние объекты в пределах указанного критического расстояния (Distance_Band_or_Threshold) получают вес 1 и влияют на расчеты для целевого объекта. Соседние объекты за пределами указанного критического расстояния получают вес 0 и не оказывают влияния на расчеты для целевого объекта.
  • ZONE_OF_INDIFFERENCE —Объекты в пределах указанного критического расстояния (Distance_Band_or_Threshold) получают вес 1 и влияют на расчеты для целевого объекта. Как только критическое расстояние превышено, веса (и влияние соседнего объекта на расчеты целевого объекта) начинают уменьшаться с расстоянием.
  • CONTIGUITY_EDGES_ONLY —Только соседние полигональные объекты, которые имеют смежную границу или перекрываются, повлияют на расчеты для целевого полигонального объекта.
  • CONTIGUITY_EDGES_CORNERS —Полигональные объекты, которые имеют общую границу, общий узел или перекрываются, повлияют на расчеты для целевого полигонального объекта.
  • GET_SPATIAL_WEIGHTS_FROM_FILE —Пространственные отношения определены в файле пространственных весов. Путь к файлу пространственных весов указан в параметре Weights_Matrix_File.
String
Distance_Method

Определяет, как рассчитываются расстояния от одного объекта до соседнего объекта.

  • EUCLIDEAN_DISTANCE —Расстояние по прямой линии между двумя точками (как ворона летает)
  • MANHATTAN_DISTANCE —Расстояние между двумя точками, измеренное вдоль осей, расположенных под прямым углом друг к другу (городские кварталы); рассчитывается суммированием абсолютных разностей между координатами х и у.
String
Standardization

Нормализация ряда рекомендуется, независимо от того, распределены ли объекты потенциально предвзято в зависимости от дизайна примера или от установленной схемы агрегации.

  • NONE —Нормализация ряда пространственных весов не применяется.
  • ROW —Пространственные веса нормализуются; каждый вес делится на его сумму ряда (сумму весов всех соседних объектов).
String
Distance_Band_or_Threshold_Distance
(Дополнительный)

Задает пороговое значение расстояния для параметров Обратное расстояние и Фиксированное расстояние. Объекты, расположенные вне указанной области, игнорируются при анализе этого объекта. Однако, для ZONE_OF_INDIFFERENCE влияние объектов, расположенных за пределами данного расстояния, сокращается с расстоянием, в то время как влияние тех объектов, которые располагаются в пределах порогового расстояния, распределяется равномерно. Введенное значение расстояния должно совпадать с расстоянием по выходной системе координат.

При использовании концептуализации обратных расстояний для вычисления пространственных отношений значение 0 обозначает, что пороговое расстояние не применялось; когда данный параметр остается пустым, при анализе рассчитывается и применяется пороговое значение по умолчанию. Значение по умолчанию – это Евклидово расстояние, которое гарантирует каждому объекту как минимум 1 соседа.

Этот параметр не оказывает никакого влияния, если выбрано примыкание полигонов (CONTIGUITY_EDGES_ONLY или CONTIGUITY_EDGES_CORNERS) либо пространственные концептуализации GET_SPATIAL_WEIGHTS_FROM_FILE.

Double
Weights_Matrix_File
(Дополнительный)

Путь к файлу, который содержит веса, определяющие пространственные и, возможно, временные отношения между объектами.

File

Производные выходные данные

NameОбъяснениеТип данных
Index

ZScore
PValue
Report_File

Пример кода

SpatialAutocorrelation, пример 1 (окно Python)

Пример скрипта окна Python для использования функции SpatialAutocorrelation.

import arcpy
arcpy.env.workspace = r"c:\data"
arcpy.SpatialAutocorrelation_stats("olsResults.shp", "Residual","NO_REPORT", 
                                   "GET_SPATIAL_WEIGHTS_FROM_FILE","EUCLIDEAN DISTANCE", 
                                   "NONE", "#","euclidean6Neighs.swm")
SpatialAutocorrelation, пример 2 (автономный скрипт Python)

Пример автономного скрипта Python для использования функции SpatialAutocorrelation.

# Analyze the growth of regional per capita incomes in US
# Counties from 1969 -- 2002 using Ordinary Least Squares Regression
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\Data"
try:
    # Set the current workspace (to avoid having to specify the full path to the feature classes each time)
    arcpy.env.workspace = workspace
    # Growth as a function of {log of starting income, dummy for South
    # counties, interaction term for South counties, population density}
    # Process: Ordinary Least Squares... 
    ols = arcpy.OrdinaryLeastSquares_stats("USCounties.shp", "MYID", 
                        "olsResults.shp", "GROWTH",
                        "LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
                        "olsCoefTab.dbf",
                        "olsDiagTab.dbf")
    # Create Spatial Weights Matrix (Can be based off input or output FC)
    # Process: Generate Spatial Weights Matrix... 
    swm = arcpy.GenerateSpatialWeightsMatrix_stats("USCounties.shp", "MYID",
                        "euclidean6Neighs.swm",
                        "K_NEAREST_NEIGHBORS",
                        "#", "#", "#", 6) 
                        
    # Calculate Moran's I Index of Spatial Autocorrelation for 
    # OLS Residuals using a SWM File.  
    # Process: Spatial Autocorrelation (Morans I)...      
    moransI = arcpy.SpatialAutocorrelation_stats("olsResults.shp", "Residual",
                        "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE", 
                        "EUCLIDEAN_DISTANCE", "NONE", "#", 
                        "euclidean6Neighs.swm")
except:
    # If an error occurred when running the tool, print out the error message.
    print(arcpy.GetMessages())

Параметры среды

Информация о лицензиях

  • ArcGIS Desktop Basic: Да
  • ArcGIS Desktop Standard: Да
  • ArcGIS Desktop Advanced: Да

Связанные разделы