Доступно с лицензией Geostatistical Analyst.
Способы создания реализаций
Геостатистическое моделирование Гаусса сначала создает сетку произвольно присвоенных значений, извлеченных из стандартного нормального распределения (среднее = 0, дисперсия = 1). Затем ковариационная модель (из вариограммы, заданной в слое простого кригинга, который необходим в качестве входных данных для моделирования) применяется к растру. Это гарантирует, что значения растра соответствуют пространственной структуре в наборе входных данных. Результирующий растр формирует одну абсолютную реализацию, и еще множество реализаций может быть создано с помощью другого растра нормально распределенных значений. Подробнее об этом методе можно узнать в публикации Дитриха и Ньюсэма (Dietrich and Newsam, 1993).
При выборе условного моделирования абсолютные растры обусловлены кригингом. Данный процесс использует кригинговую оценку (прогноз) в каждом местоположении для того, чтобы смоделированные значения использовали значения входных данных, а кригинговые проинтерполированные значения в среднем реплицированы. Подробнее об условиях реализаций с помощью кригинга может узнать в публикации Джонела (Journel, 1974).
Но если в модель простого кригинга включена погрешность измерения, то значения входных данных не будут использоваться (в слое простого кригинга или в смоделированных реализациях). Кроме того, инструмент Геостатистическое моделирование Гаусса может использоваться для непрерывной или сглаженной окрестности поиска, во избежание неоднородности в моделируемых поверхностях из-за изменения в локальной окрестности, которая используется в кригинге. Подробнее об этом можно узнать в публикации Элдворса, Грибова и Криворучко (Aldworth (1998), Gribov and Krivoruchko (2004)).
Более детально ознакомиться с концепциями геостатистического моделирования и примерами условного и абсолютного моделирования можно в разделе справки основные концепции геостатистического моделирования.
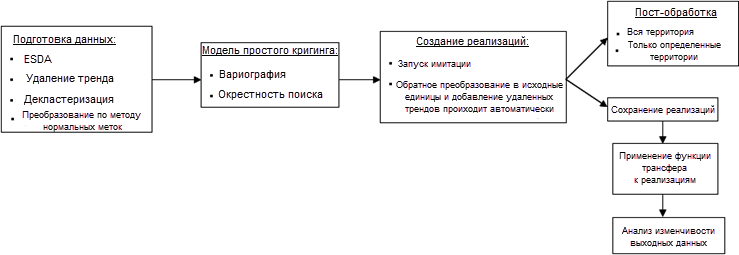
Общий рабочий процесс для геостатистического моделирования Гаусса включает подготовку данных, создание реализаций, обратное преобразование результатов в исходные единицы измерения и повторную обработку результатов и/или использование результатов в качестве входных данных в функцию преобразования (модель) для оценки вариабельности в выходных данных модели. Этот процесс представлен на рисунке ниже.
Модель простого кригинга для моделирования
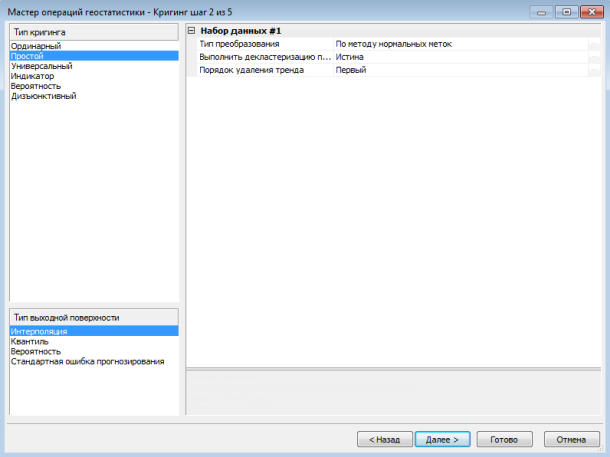
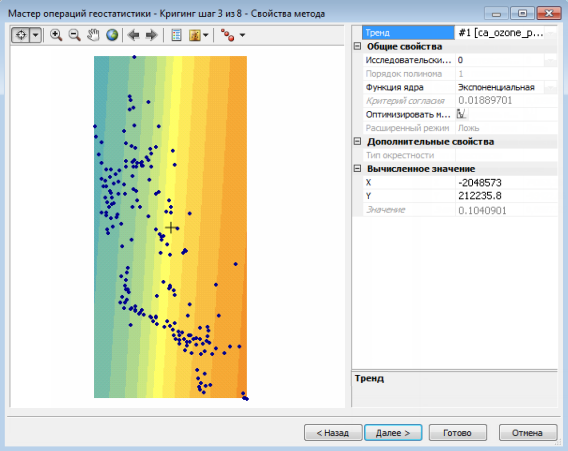
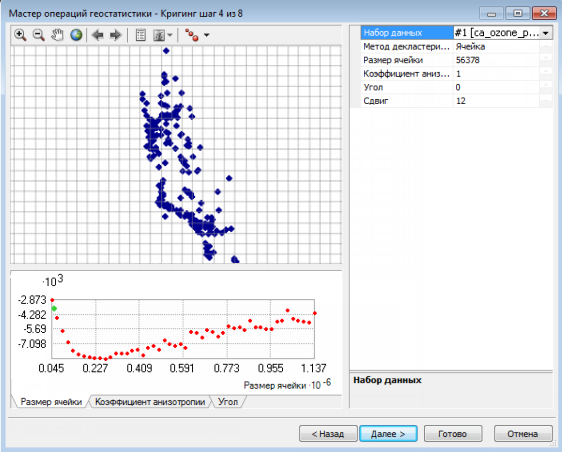
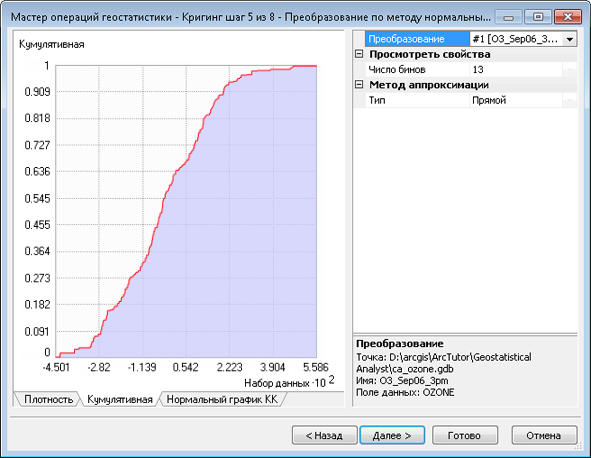
Инструмент Геостатистическое моделирование Гаусса принимает любую модель простого кригинга. Но результаты моделирования являются верными, только если входные данные, используемые для подбора модели вариограммы и определения условий реализаций, нормально распределены. Этого можно достичь, применив преобразование по методу нормальных меток. Чтобы получить типичную гистограмму из кластерных данных, необходимо выполнить декластеризацию. Для обеспечения стационарности среднего значения в пространственной области данных нужно удалить тренды. Данные действия продемонстрированы на рисунке ниже. На рисунке (a) представлены выбранные опции: простой кригинг с удаленным трендом, декластеризацией и преобразованием по методу нормальных меток. На рисунке (b) показан тренд, который будет удален из набора данных перед выполнением декластеризации, преобразования по методу нормальных меток и вариографии. На рисунке (c) изображена декластеризация по ячейкам. На рисунке (d) представлено преобразование по методу нормальных меток, которое в данном случае использует прямой метод.
Проверка выходных данных моделирования
Реализации необходимо проверить на подтверждение следующих фактов:
- Значения выходных данных, их пространственные структуры и местоположения допустимы.
- Гистограмма имитированных данных в среднем воспроизводит гистограмму входных данных.
- Гистограмма имитированных данных в среднем воспроизводит гистограмму входных данных.
- Для условного моделирования используются значения входных данных (если модель простого кригинга не включает погрешность измерения).
Повторная обработка
После создания реализаций они, как правило, обрабатываются повторно для получения итоговой информации по результатам. Инструмент Геостатистическое моделирование Гаусса предоставляет несколько опций повторной обработки, которая может производиться на всем пространственном экстенте растров или в конкретной исследуемой области. Такие области определяются путем задания полигонального класса объектов для опции Входные полигоны статистики. Выходные данные подобны в обоих случаях: повторная обработка всех растров создает итоговые растры, в то время как повторная обработка полигональных областей создает полигональный выходной класс объектов, которые содержат итоговые статистические величины для каждого полигона.
Повторная обработка всего экстента растра
- Выходные растры включают в себя минимальное значение, генерируемое для каждого местоположения (ячейки), а также максимальное, среднее значение, стандартное отклонение, первый квартиль для каждой ячейки, значение медианы (второго квартиля) и третий квартиль. Кроме того, можно задать квантиль, возвращающий значение, соответствующее этому квантилю, основанному на распределении значений, смоделированных в каждой ячейке. Также можно задать пороговое значение, которое будет возвращать процент смоделированных значений, превышающих порог.
- Заметьте, что повторно обрабатываемый экстент может лимитироваться заданием ограничивающего полигона или набором точек (в этом случае генерируется выпуклая оболочка, которая используется в качестве ограничивающего полигона). Значения моделируются только в пределах ограничивающего полигона.
Повторная обработка исследуемых областей
- После задания исследуемых областей полигонов в выходные данные для каждого полигона будут автоматически включены итоговые статистические величины, которые описаны в таблице ниже. Кроме того, можно задать значения квантиля и пороговое значение (например, при повторной обработке всего экстента растра). Также описаны в таблице выходные данные, сформированные с этими установленными опциями.
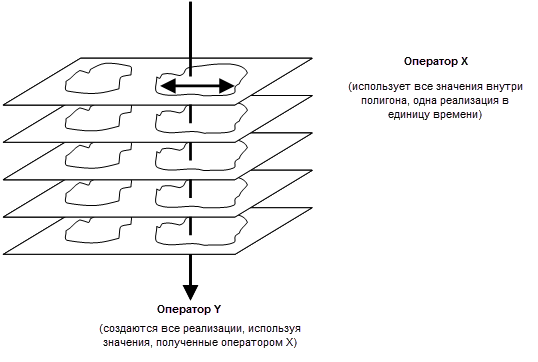
- Итоговые выходные данные для полигонов рассчитаны при использовании операторов, которые представлены на рисунке ниже. Оператор Х использует все значения, которые попадают в полигон, и рассчитывает значение для каждой реализации. Оператор Y использует значения из всех реализаций. Входными данными для оператора Y являются значения для областей полигона каждой реализации, рассчитанные оператором Х.
Назначения полей в выходном классе объектов перечислены в следующей таблице.
| Имя поля | Описание |
|---|---|
MIN | Минимальное значение любой ячейки во всех реализациях, которые лежат внутри полигона. |
Макс. | Максимальное значение любой ячейки во всех реализациях, которые лежат внутри полигона. |
MEAN | Среднее значение всех ячеек во всех реализациях, которые лежат внутри полигона. |
STDDEV | Среднеквадратическое отклонение всех ячеек во всех реализациях, которые лежат внутри полигона. |
QUARTILE1 | Значение первого квартиля всех ячеек во всех реализациях, которые лежат внутри полигона. |
MEDIAN | Значение медианы всех ячеек во всех реализациях, которые лежат внутри полигона. |
QUARTILE3 | Значение третьего квартиля всех ячеек во всех реализациях, которые лежат внутри полигона. |
QUANTILE | Значение, соответствующее определенному пользователем квантилю, для всех ячеек во всех реализациях, которые лежат внутри полигона. |
P_THRSHLD | Процент ячеек, превышающих заданное пользователем пороговое значение, по всем ячейкам во всех реализациях, которые лежат внутри полигона. |
X_Y | Функция Х одновременно применяется к значениям ячеек, которые находятся внутри полигона, и одной реализации. Этот процесс соответствует работе инструмента Зональная статистика при одновременном использовании полигона в качестве зоны и одной реализации в качестве сетки значений. Функция Y применяется к значениям, генерируемым функцией Х.
|
CELL_COUNT | Количество ячеек, которые лежат внутри полигона. Если центр ячейки находится внутри полигона, то считается, что ячейка находится в полигоне. Отрицательное число указывает на то, что часть полигона находится вне экстента смоделированного растра и/или часть полигона расположена за пределами вырезающей границы. Отрицательное число само по себе показывает общее число ячеек, которые лежат внутри полигона. |
SOURCE_ID | Объект или идентификатор объекта входного полигонального класса объектов. |
Для ограничивающего полигона и исследуемых областей полигона ячейки растра считаются расположенными внутри полигонов, если центр ячейки находится внутри границы полигона.
Пример условного моделирования и повторной обработки выходных данных
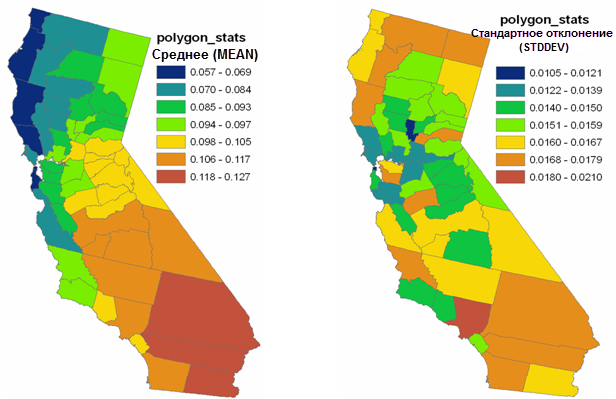
На следующем рисунке представлены результаты условного моделирования с повторной полигональной обработкой выходных данных. На картах отображено среднее значение и стандартное отклонение 100 реализаций значений концентрации озона для каждого округа в штате Калифорния. Среднее значение и значение стандартного отклонения могут использоваться, например, в эпидемиологических исследованиях, где случай заболевания необходимо сверять со средним значением концентрации озона для каждого округа.
Ссылки и дополнительная литература
Aldworth, J. 1998. Пространственная интерполяция, Пространственная выборка и Ошибка измерения. Ph.D. Тезис, Университет штата Айова. 186.
Chiles J. P. и P. Delfiner. 1999. Геостатистика: Моделирование пространственной неопределенности. Нью Йорк: John Wiley & Sons, 449–471.
Deutsch, C.V., и A. G. Journel. 1998. GSLIB Geostatistical Software Library and User's Guide, 2nd edition. New York: Oxford University Press, 119–141.
Dietrich, C. R. и G. N. Newsam. 1993. "A Fast and Exact Method for Multidimensional Gaussian Stochastic Simulations." Water Resources Research 29 (8): 2861–2869.
Goodchild, M. F., B. O. Parks и L. T. Steyaert. 1993. Environmental Modeling with GIS. New York: Oxford University Press, 432–437.
А. Грибов и К. Криворучко. 2004. "Geostatistical Mapping with Continuous Moving Neighborhood." Mathematical Geology 36 (2): 267–281.
Journel, A. G. 1974. "Геостатистика для условного моделирования рудных тел." Economic Geology 69: 673–687.
Leuangthong, O., J. A. McLennan и C. V. Deutsch. 2004. "Minimum Acceptance Criteria for Geostatistical Realizations." Natural Resources Research 13 (3): 131–141.