需要 Geostatistical Analyst 许可。
开始本练习前，您应该已经完成练习 1。
在本练习中，您将浏览数据。如同在练习 1 结尾显示的结构化过程所建议的那样，要在创建表面时做出更好的决策，应该首先浏览数据集以便对其有一个更好的理解。浏览数据时，在值中查找会显著影响到输出预测表面的明显错误；检查数据的分布情况；查找全局趋势、方向影响等。
Geostatistical Analyst 提供了多种数据浏览工具。在本练习中，您将以三种方式浏览数据：
- 检查数据的分布。
- 识别数据中的趋势（如果存在）。
- 了解空间自相关和方向影响。
使用“直方图”工具检查数据的分布。
如果数据呈正态分布（钟形曲线），则用于生成表面的插值方法可提供最佳结果。如果数据呈偏斜（倾向一侧）形状，则可以选择变换数据使其呈正态分布。因此，在创建表面之前，了解数据的分布情况非常重要。通过“直方图”工具为数据集中的属性绘制的频数直方图可以检查数据集中每个属性的一元（一个变量）分布。接下来，您将浏览 O3_Sep06_3pm 图层的臭氧分布。
- 如果已关闭前一次 ArcMap 会话，则再一次启动该程序并打开 Ozone Prediction Map.mxd。
- 单击 ca_outline 图层并将其拖放到内容列表中的 O3_Sep06_3pm 图层下。
内容列表示例 - 单击 O3_Sep06_3pm 图层以选择此图层。
- 在 Geostatistical Analyst 工具条上，单击 Geostatistical Analyst > 探索数据 > 直方图。
“探索数据”菜单中的“直方图” - 在直方图 对话框中，单击属性箭头，然后选择 OZONE。
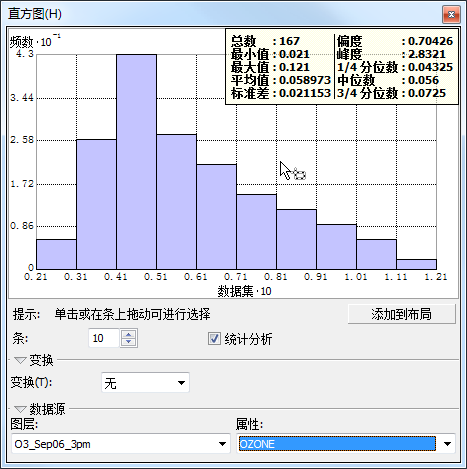
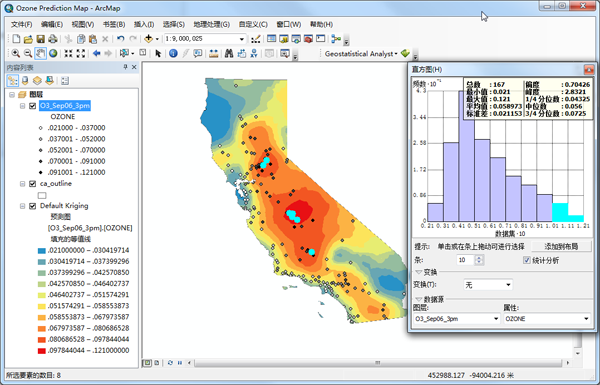
直方图 为了便于阅读，x 轴上的值已经按系数 10 重新进行了调整。您可能要重新调整“直方图”对话框的大小并移动其位置，以便可同时看到地图，如下图所示。
直方图 在直方图中，臭氧值的分布以分成 10 个级别的臭氧值范围加以描述。每个级别中数据的频数以各条块的高度表示。通常，分布的重要特征包括中心值、偏离程度和对称度。作为一种快速检查手段，如果平均值和中值近似相同，则初步表明数据可能呈正态分布。
该臭氧数据直方图表示数据为单峰（一个高峰）并且向右偏移。分布图的右侧尾部表示存在的采样点相对较少但臭氧浓度值较高。似乎该数据不接近于正态分布。
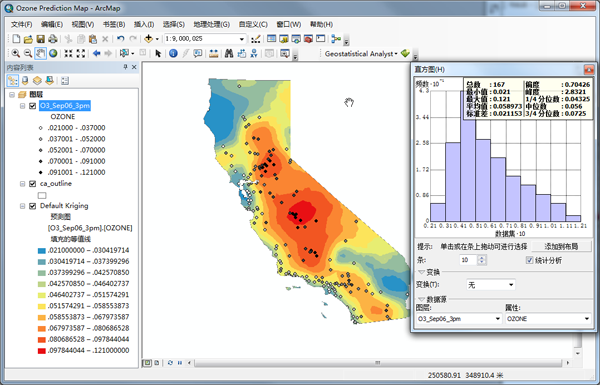
- 通过单击并在其上方拖动光标来选择那两个臭氧值大于 0.10 ppm 的直方图条块（别忘了这些值已经按系数 10 做过重新调整）。
同时地图上会对应选择处于此范围内的采样点。您可能会注意到，这些采样点中的大多数位于加利福尼亚州的中央峡谷中。
显示所选点的直方图和地图 - 单击基础工具 工具条上的清除所选要素按钮
以清除地图和直方图上的所选点。 - 单击直方图 对话框右上角的关闭按钮。
创建正态 QQ 图
分位数-分位数 (QQ) 图用于将数据的分布与标准正态分布进行比较，它提供了另一种测量数据正态分布的方法。这些点与图中呈 45 度的直线间的距离越近，这些样本数据越接近于正态分布。
- 在 Geostatistical Analyst 工具条上，单击 Geostatistical Analyst > 探索数据 > 正态 QQ 图。
“探索数据”菜单中的“正态 QQ 图” - 单击属性箭头，然后选择 OZONE。
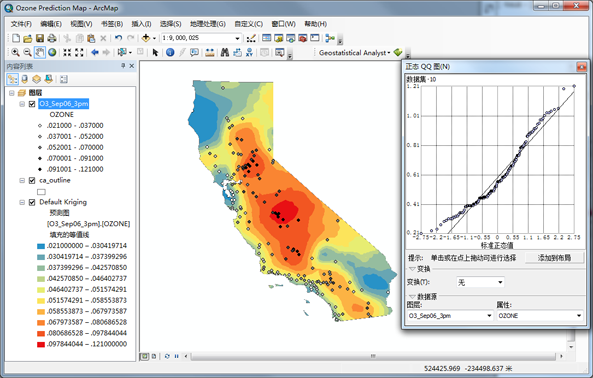
“正态 QQ 图”地图 常规的 QQ 图是两个分布的分位数对照绘制出的一种图。对于两个相同的分布，QQ 图将是一条直线。因此，可以通过对照绘制数据的分位数与标准正态分布的分位数来检查臭氧数据的正态分布。从上述的正态 QQ 图中，您可以看到该图并不是非常接近于一条直线。与此线的主要偏离发生在低臭氧浓度值处（在上图中选中并以绿色显示，已通过在这些臭氧浓度值的上方单击并拖动光标来选择它们）。
如果这些数据在直方图或正态 QQ 图中未呈现正态分布，可能必需对这些数据进行转换使其符合正态分布，然后再应用某些克里金法插值技术。
- 单击位于正态 QQ 图 对话框右上角的关闭按钮。
识别数据中的全局趋势
如果在数据中存在趋势，则该趋势就是可以通过数学公式表示的表面的非随机（确定性）组成部分。例如，可以通过平面表示一个平缓的山坡。山谷可以使用更复杂的公式（二阶多项式）通过创建 U 形来表示出来。通过此公式可以生成所需表面的制图表达。但是，多数情况下公式生成的表面过于平滑，而无法准确地描述实际情况，因为没有山坡是理想的平面，也没有任何山谷是理想的 U 形。通过以下步骤可以将局部变化添加到表面，即，使用其中某个平滑函数为趋势建模、从数据中移除趋势并通过为残差（移除趋势后的剩余部分）建模继续进行分析。为残差建模时，您将分析表面中的短程（局部）变化。通过“趋势分析”工具可以识别输入数据集中存在的/不存在的趋势，并且可以识别出最佳拟合此趋势的多项式阶数。
- 在 Geostatistical Analyst 工具条上，单击 Geostatistical Analyst > 探索数据 > 趋势分析。
“探索数据”菜单中的“趋势分析” - 单击属性箭头，然后选择 OZONE。
趋势分析图中的每个垂直杆对应表示一个臭氧测量的位置和值（高度）。这些数据点都投影到垂直平面上，即，东西向平面和南北向平面。穿过这些投影点绘制出一条最佳拟合线（多项式），显示特定方向上的趋势。如果此线是平的，则表示不存在趋势。但是，如果观察下图中浅绿色的线，可以看到该线从低值开始，其值随着该线向 x 轴的中心移动而增加，随后下降。与此类似，蓝线的值随着此线向北移动而增加，并且从该州的中心开始下降。这就说明数据似乎从数据值域的中心向所有方向都呈现了很强的趋势。
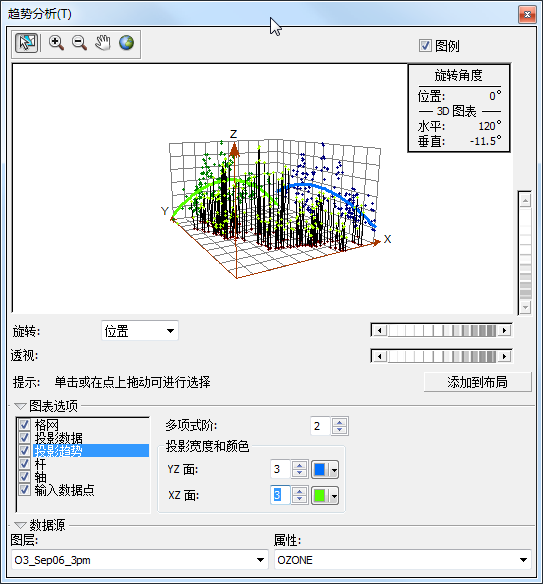
趋势分析图 - 单击旋转位置滚动条并且向左滚动直到旋转角度为 90 度。
旋转滚动条 可以看到在旋转这些点时，趋势始终呈现为倒置的 U 形。此外，对于任何特定的旋转角度，该趋势似乎并未表现出更强的趋势（更明显的 U 形），再次印证了之前的观察结果，即从数据值域的中心向所有方向都呈现了很强的趋势。由于此趋势为 U 形，因此将二阶多项式用作全局趋势模型是不错的选择。产生此趋势的可能原因是：海岸地区的人口较少，而较远的内陆地区人口众多，通往山区时人口又逐渐减少。在练习 4 中，您将移除这些趋势。
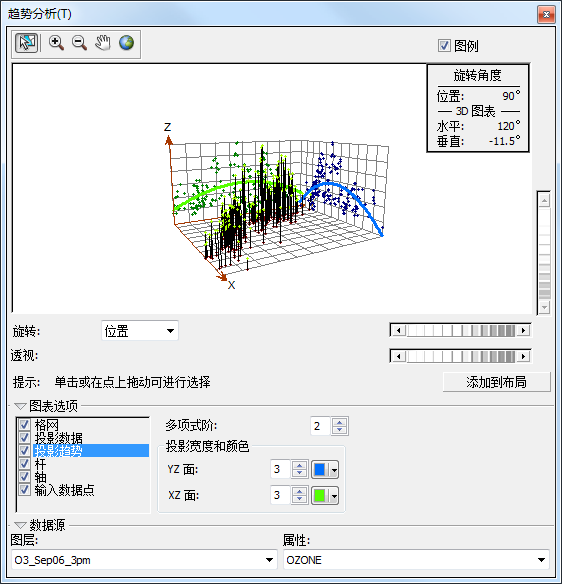
旋转 90 度的趋势分析图 - 单击位于趋势分析 对话框右上角的关闭按钮。
浏览空间自相关和方向影响
- 在 Geostatistical Analyst 工具条上，单击 Geostatistical Analyst > 探索数据 > 半变异函数/协方差云。
“探索数据”菜单中的“半变异函数/协方差云” - 单击属性箭头，然后选择 OZONE。
通过半变异函数/协方差云可以检查测量样本点之间的空间自相关。通常假定，相互之间越接近的事物就越相似。通过半变异函数/协方差云可以检查此关系。为此，在 y 轴上相对于分隔每对测量值的距离（在 x 轴上绘制）绘制半变异函数值（每个位置对的值的差值平方）。
在半变异函数/协方差云中的每个红色圆点表示一个位置对。因为相互之间越接近的位置就应该越相似。在半变异函数图中，相互之间最接近的位置（在 x 轴的最左侧）应该具有较小的半变异函数值（y 轴上的低值）。随着位置对之间的距离增加（在 x 轴上向右移动），半变异函数值也应该增加（在 y 轴上向上移动）。但当到达某个距离时云会变平，这表示相互间的距离大于此距离的点对的值不再相关。
观察半变异函数图，如果出现某些非常接近的数据位置（在 x 轴上接近零）却具有高于预期的半变异函数值（在 y 轴上的高值），则应该调查这些位置对，看一下是否存在不准确的数据。
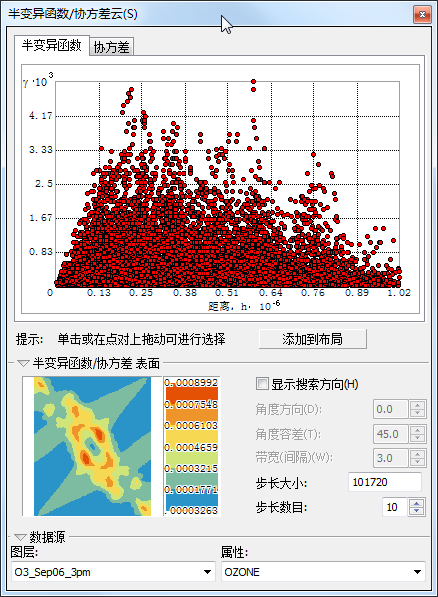
半变异函数云 - 在基础工具 工具条上单击通过矩形选择要素按钮
，然后在半变异函数/协方差云 对话框中某些具有较大的半变异函数（y 轴）值的点的上方单击并拖动光标以选择这些点。（使用左侧的图作为指导。选择的点不需要与下图所示的点完全相同。）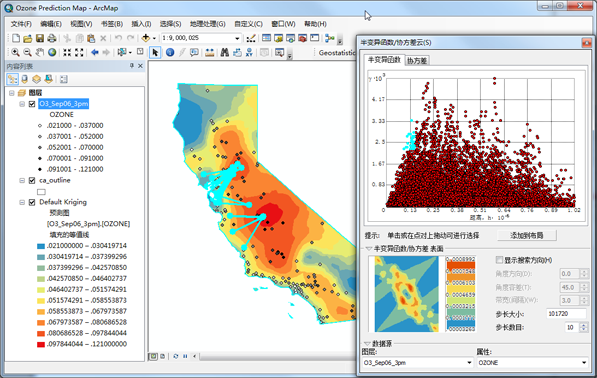
点选择示例 1 在半变异函数图中选择的采样位置对高亮显示在地图上，连线位置对的线指示配对关系。正如可从默认的克里金预测地图预想到的，在某个位置对中的各点之间特定距离上具有高的半变异函数值的连线与臭氧值中最大梯度相对应。
下图显示了具有典型半变异函数值的位置对，其点对之间的距离大致相同。
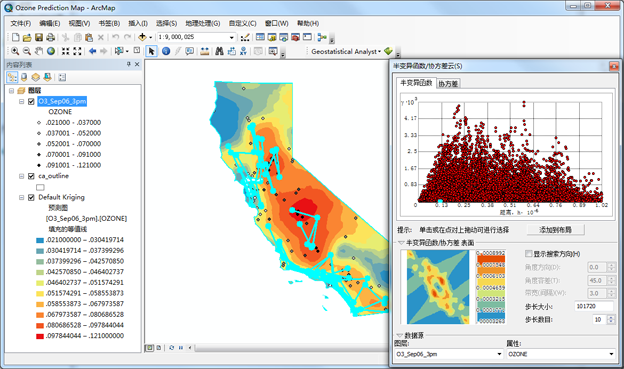
点选择示例 2 - 选中显示搜索方向。
- 单击并将方向光标移动到任一角度。
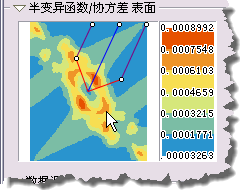
方向光标示例 光标所指向的方向决定了将在半变异函数图上绘制的数据位置对。例如，如果光标指向东西方向，将仅在半变异函数上绘制其相互之间处于东或西方向上的数据位置对。这样可以排除您不感兴趣的位置对并且可以浏览施加于数据上的方向影响。
- 单击并沿着具有最高半变异函数值的位置对拖动通过矩形选择要素工具，以便在半变异函数图和地图中选择这些位置对。（以下图作为指导。不必选择与下图中相同的点，也无需使用相同的搜索方向。）
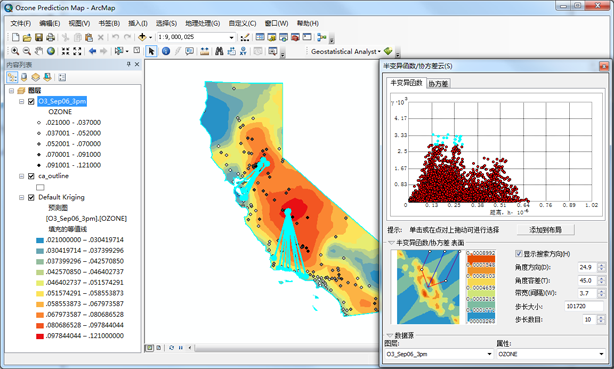
半变异函数云选择示例 请注意，大多数连接的位置（用于表示地图上的点对）对应于加利福尼亚州中部区域的采样点之一。这是因为此区域的臭氧值高于加利福尼亚州的任何其他地区。
- 单击位于该对话框右上角的关闭按钮。
- 单击基础工具 工具条上的清除所选要素按钮 ，以清除地图上的所选点。
在本练习中，您已经学习了以下内容
- 臭氧数据为单峰，但并不是非常接近于正态分布，如直方图中所示。
- 正态 QQ 图也显示出数据不呈正态分布，因为图中的点没有形成一条直线。可能需要进行数据转换。
- 通过“趋势分析”工具可以看到数据呈现一种趋势，将该趋势细化后，可以看出二阶多项式是对其进行的最佳拟合。
- 半变异函数/协方差云说明了极高的半变异函数值大部分以垂直于海岸线的连线表示。使用此工具进行的分析表明插值模型应该考虑到各向异性。
- 半变异函数表面表示在数据中存在空间自相关。在已知数据集中不存在异常（或错误）的采样点的前提下，可在对表面插值有把握的情况下继续进行操作。与在练习 1 中使用默认选项和参数值创建的表面相比，您将能够创建更为精确的表面，因为您现在已经了解到在数据中存在趋势和各向异性，并且可在插值中对其进行调整。此外，通过数据转换也可以改进预测模型。
在练习 3 中，您将使用所了解到的关于臭氧的数据来创建一个比在练习 1 中根据默认参数值创建的模型更好的插值模型。