需要 Spatial Analyst 许可。
溶质在孔隙介质中的传输涉及两个主要机制:移流和水动力学弥散。移流描述了溶质随传输液体进行的被动传输。弥散是由于流体在孔隙空间内的差异运动而将溶质和流体混合在一起的过程。孔隙扩散假定蓄水层垂直混合,即整个垂直部分内的浓度相同。这样便可按栅格数据模型的要求,应用二维数学模型。
二维弥散
孔隙介质中的二维弥散由移流-弥散方程(Bear,1979;Freeze 和 Cherry,1979;Marsily,1986)控制,该方程依纵向(流向)XL 和横向(垂直于流向)XT 建立,如下所示:
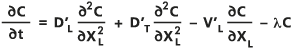
- 其中:
C:溶质浓度(作为两个空间维度和时间 t 的函数)。
∂C/∂t:表示时间导数。
D'L:纵向有效(延迟)弥散系数。
D'T:横向有效(延迟)弥散系数。
λ:衰变系数,假定为一阶指数衰变的常量。
弥散系数
弥散系数可衡量溶剂在指定方向的扩散范围。
D'i = Di/R
- 其中:
R:延迟因子。
i:方向(纵向或横向)。
弥散系数与溶质在特定介质中的行为有关。
弥散性与弥散系数之间的关系
弥散性 αL(纵向弥散性)和 αT(由弥散比得出)与弥散系数的关系如下:
D'L = αL V' 和
D'T = αT V'
其中:
V':扩散的平均延迟速度。
XL:纵向位移,平行于质心处的流向。
XT:横向位移,垂直于质心处的流向。
V'L:纵向延迟溶质速度。
传输速度
在地下水流中:
V = q / n
- 其中:
q:达西通量(单位横断面面积的排水量)。
n:地质构造的有效孔隙度。
V' = V / R
有关传输速度的详细信息,请参阅达西速度的文档。
高斯弥散
此孔隙扩散方程的近似解基于一个假设,即二维域中初始浓度为零的瞬时点源高斯弥散(例如,洁净且垂直混合的蓄水层)。使用以下方程计算近似解:
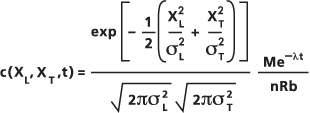
- 其中:
M:源处瞬间释放的溶质质量,采用质量单位。
n:蓄水层孔隙度。
R:延迟因子。
b:蓄水层厚度(采用长度单位)。
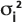 :纵向和横向的高斯分布的方差,指定为所提供的纵向弥散性和弥散比以及从追踪文件中获取的溶质质心的行进路径长度的函数。
:纵向和横向的高斯分布的方差,指定为所提供的纵向弥散性和弥散比以及从追踪文件中获取的溶质质心的行进路径长度的函数。
此二元高斯分布函数的常规椭圆形如下所示:
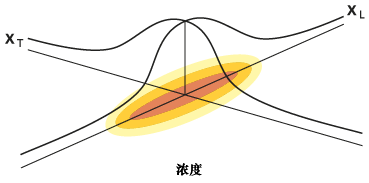
孔隙扩散的解存在几个明显限制,而且其中还隐含假设。弥散椭圆位于溶质的质心,并假定其已经沿着输入文件中所描述的流动追踪进行移动。椭圆的方向也固定为流动追踪,同时主轴与质心处的追踪相切。对于同样会对分布产生影响孔隙度和厚度,会在其各自栅格的质心处对其进行插值,且不会加入任何周围像元信息。您可以提供延迟、时间、衰变系数、纵向弥散性及弥散比等常量。
弥散性
弥散性是用于控制溶质在孔隙介质中弥散的参数,使用长度单位指定。在孔隙扩散模型中,弥散性用于计算上述高斯弥散方程的方差 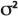 ,具体根据:
,具体根据:
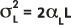 和
和 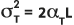
弥散性的本质及用于确定弥散性的方法是地下水建模届备受关注及争论不休的话题,但目前尚未找到一种普遍接受的用于估计弥散性值的方法。可在 Gelhar 等 (1992) 所著文章中找到有关各种地质构造中的弥散性的论述。
下图对已出版的文献资料中的各种数据进行了总结,并将纵向弥散性与感兴趣问题的比例进行了关联,表示从源位置到观测点的距离。
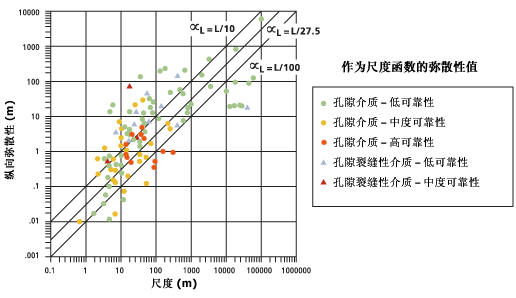
图像的实线(中心线)表示通过“孔隙扩散”工具计算出的纵向弥散性的默认值。
该线的创建方式是通过将
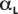 线性回归拟合为 L,得到
线性回归拟合为 L,得到 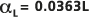 或
或 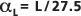 ,其中行进路径的长度 L 为观测比例。
,其中行进路径的长度 L 为观测比例。此回归的统计数据如下所示。外部虚线位于
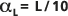 和
和 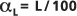 处,以便进行比较。
处,以便进行比较。
此默认计算应仅供指导,因为一些研究人员并不赞成使用此类通用拟合。对于任何特定的比例或站点,有效的弥散性可能覆盖两个数量级的范围,而且更加可靠的估计值往往是较低的值。您应该使用一定范围的弥散性值执行数次模拟操作,而不是使用没有理论基础的默认值。与使用一次模拟的结果相比,考虑一组结果会更为有效。
上述说明同样适用于下图所示的纵横弥散比的估计。这些值一般会通过一个简单比率相关联,不过,仍应使用一定范围的值进行试验。
弥散性比较
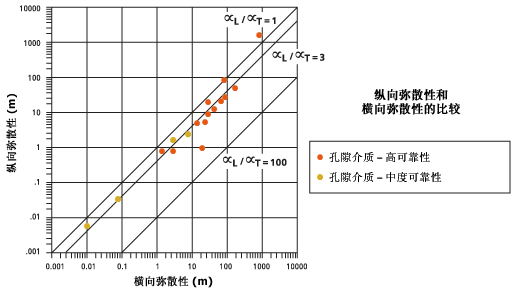
默认弥散比 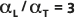 在下图中通过实线(中心线)表示。虚线(外部线)位于
在下图中通过实线(中心线)表示。虚线(外部线)位于 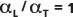 和
和 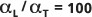 处,以便进行比较。
处,以便进行比较。
有效孔隙度和导水系数值
Gelhar 等在表格中提供有效孔隙度和导水系数。在 Freeze 和 Cherry (1979) 及 Marsily (1986) 所著文章中可以找到这些值的表。
延迟
延迟是传输液体的速度与溶质速度的比值,以 1 到无穷大范围内的数字表示,该值不具有单位。值为 2 的延迟表示溶质以渗流速度的一半在孔隙介质中迁移。理想的示踪剂不会受到吸附,并且会在溶液中随液体行进。此类溶质的延迟值为 1,表示溶质和传输液体的移动速率相同。
此现象是多孔基体对成分吸附和解吸作用的结果。多孔基体为孔壁上的有机涂层时,此现象尤为明显。Freeze 和 Cherry (1979) 的论述中对延迟方程进行了介绍,具体如下:
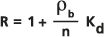
其中:
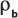 :基体体积密度。
:基体体积密度。n:结构的孔隙度。
Kd:分布系数,表示因液相和固相间(假设线性等温线)的快速可逆溶质吸附导致的分离现象。
Marsily (1986) 也对延迟因子和吸附作用进行了详细论述。
执行移流-弥散建模
达西流、粒子追踪和孔隙扩散工具可用于对地下水中的成分进行基本的移流-弥散建模。达西流用于根据地质数据生成地下水流速场;粒子追踪用于计算从点源开始通过流场的移流路径;孔隙扩散用于计算在沿流路径移流时瞬时点释放某种成分的水动力学弥散。
有关使用这些功能构建移流-弥散模型的完整论述,请参阅 Tauxe (1994)。
地下水建模的典型顺序为,依次执行达西流、粒子追踪和孔隙扩散。
示例
- 以下是孔隙扩散工具对话框的示例:
输入粒子追踪文件:ttrack.txt
输入有效地层孔隙度栅格数据:poros
输入饱和浓度栅格数据:thickn
输出栅格:ppuff1
质量:3.2e7
弥散时间:50000
纵向弥散性:6
弥散比:3
延迟因子:1
衰变系数:250
- 在地图代数中使用孔隙扩散的示例:
outPPuff1 = PorousPuff(ttrack.txt, poros, thickn, 1000000, 0.01, 10, 1.5, 1.0, 500)
- 以下是涉及地下水建模工具套件的一系列地图代数表达式:
out_vol = DarcyFlow(head, poros, thickn, transm, dir1, mag1) ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, "#", "#", track_feat.shp) out_puff = PorousPuff(ttrack.txt, poros, thickn, 3.2e7, 50000, 6, 3, 1, 250)
参考文献
Bear, J. 1979, Hydraulics of Groundwater. McGraw–Hill.
Freeze, R. A., and J. A. Cherry. 1979. Groundwater. Prentice–Hall.
Gelhar, L. W., C. Welty, and K. R. Rehfeldt. 1992. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research 28 (7): 1955-1974.
Marsily, G. de. 1986. Quantitative Hydrogeology. Academic Press.
Tauxe, J. D. 1994. "Porous Medium Advection–Dispersion Modeling in a Geographic Information System". Ph.D. diss., University of Texas, Austin.