大多数统计检验在开始时都首先确定一个零假设。模式分析工具(“分析模式”工具集和“聚类分布制图”工具集)的零假设是完全空间随机性 (CSR),它或者是要素本身的完全空间随机性,或者是与这些要素关联的值的完全空间随机性。模式分析工具所返回的 z 得分和 p 值可帮助您判断是否可以拒绝零假设。通常,您将运行其中一种模式分析工具,并希望 z 得分和 p 值表明可以拒绝零假设,这就意味着:您的要素(或与要素关联的值)表现出统计意义上的显著性聚类或离散模式,而不是随机模式。如果您在景观分布(或空间数据)中发现了空间结构(如聚类),就证明某些基础空间过程在发挥作用,而这方面通常正是地理学者或 GIS 分析人员所最为关注的。
p 值表示概率。对于模式分析工具来说,p 值表示所观测到的空间模式是由某一随机过程创建而成的概率。当 p 很小时,意味着所观测到的空间模式不太可能产生于随机过程(小概率事件),因此您可以拒绝零假设。您可能会问这样的问题:要小到什么程度才算足够小?这是一个非常好的问题。请参见下面的表和内容论述。
Z 得分表示标准差的倍数。例如,如果工具返回的 z 得分为 +2.5,我们就会说,结果是 2.5 倍标准差。如下所示,z 得分和 p 值都与标准正态分布相关联。
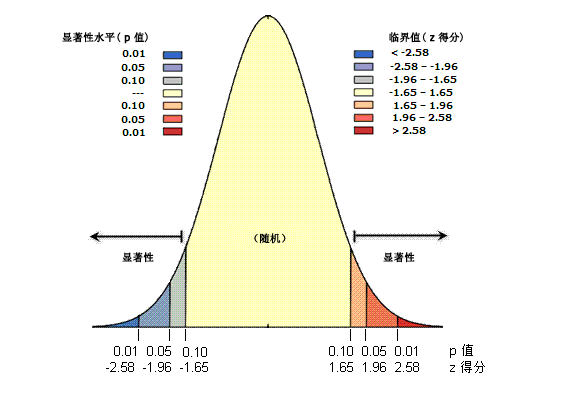
在正态分布的两端出现非常高或非常低(负值)的 z 得分,这些得分与非常小的 p 值关联。当您运行要素模式分析工具并由该工具得到很小的 p 值以及非常高或非常低的 z 得分时,就表明观测到的空间模式不太可能反映零假设 (CSR) 所表示的理论上的随机模式。
要拒绝零假设,您必须对所愿承担的可能做出错误选择(即错误地拒绝零假设)的风险程度做出主观判断。因此,请先选择一个置信度,然后再执行空间统计。典型的置信度为 90%、95% 或 99%。这种情况下,99% 的置信度是最保守的,这表示您不愿意拒绝零假设,除非该模式是由随机过程创建的概率确实非常小(低于 1% 的概率)。
置信度
下表显示了不同置信度下未经校正的临界 p 值和临界 z 得分。
| z 得分(标准差) | p 值(概率) | 置信度 |
|---|---|---|
< -1.65 或 > +1.65 | < 0.10 | 90% |
< -1.96 或 > +1.96 | < 0.05 | 95% |
< -2.58 或 > +2.58 | < 0.01 | 99% |
请考虑一个示例。置信度为 95% 时,z 得分的临界值为 -1.96 和 +1.96 倍标准差。同时,与其关联的未经校正的 p 值为 0.05。如果 z 值在 -1.96 和 +1.96 之间,则未经校正的 p 值将大于 0.05,因而不能拒绝零假设,因为所表现出的模式很可能是随机空间过程产生的结果。如果 z 得分在该范围之外(例如,-2.5 或 +5.4 倍标准差),则所观测到的空间模式可能过于罕见,不可能是随机过程产生的结果,而且 p 值很小也可以反映出这一点。在这种情况下,可以拒绝零假设,并着手找出是什么可能导致您的数据出现具有统计显著性的空间结构。
这里的一个关键概念是,正态分布中间位置的值(例如,类似 0.19 或 -1.2 的 z 得分)代表了预期的结果。但在 z 得分的绝对值很大而概率很小时(即出现在正态分布的两端),您就会查看其中存在的不寻常现象并且这也非常有趣。例如,对于热点分析工具,不寻常意味着出现了具有统计显著性的热点或冷点。
FDR 校正
局部空间模式分析工具(包括热点分析和聚类和异常值分析 (Anselin Local Moran's I))提供了一个可选的布尔型参数应用错误发现率(FDR)校正。如果选中该参数,错误发现率 (FDR) 过程可能会减小上表所示的临界 p 值阈值以兼顾多重测试和空间依赖性。减少值(如果存在)是所采用的输入要素数量和邻域结构的一小部分。
局部空间模式分析工具的工作原理是:考虑临近要素环境中的各个要素并确定局部模式(目标要素及其相邻要素)与全局模式(数据集中的所有要素)在统计学上是否不同。与各个要素关联的 z 得分和 p 值结果将确定该差异是否具有统计显著性。此分析方法同时导致多重测试和空间依赖性方面的问题。
多重测试 - 当置信度为 95% 时,根据概率论我们可知 100 种情况中存在 5 种情况空间模式会呈现某种结构(如聚类或离散)并在统计显著性方面与 p 值关联,而事实上促成该模式的基础空间过程是完全随机的。在此类情况下,我们可能会由于 p 值存在统计显著性而错误地拒绝 CSR 零假设。如果不考虑局部空间统计对数据集中的每个要素执行一次测试,5% 的可能性似乎还相当保守。例如,如果存在 10000 个要素,预计会出现多达 500 个错误结果。
空间依赖性 - 相互接近的要素往往较为相似;空间数据通常会揭示这种依赖性。但是,很多统计测试需要要素是独立的。对于局部模式分析工具而言,这是由于空间依赖性会人为地夸大统计显著性。空间依赖性在使用局部模式分析工具时更为严重,因为各个要素在其相邻要素环境内进行评估,而相互接近的要素可能共享很多相同的相邻要素。这种重叠会加重空间依赖性。
至少有三种方法可以解决多重测试和空间依赖性问题。第一种方法是以如下原则为指导忽略相应的问题:对数据集中各要素执行的单个测试应该孤立看待。但如果使用这种方法,一些具有统计显著性的结果很有可能是不正确的(似乎具有统计显著性而实际上基础空间过程是随机的)。第二种方法是应用经典的多重测试步骤(如 Bonferroni 校正或 Sidak 校正)。但这些方法通常过于保守。虽然它们能够显著降低误报的数量,但也会漏掉某些确实存在的具有统计显著性的结果。第三种方法是应用 FDR 校正,FDR 校正针对给定的置信度来计算误报的数量并相应地调整临界 p 值。使用该方法时,具有统计显著性的 p 值按照从最小(最强)到最大(最弱)的顺序排序,并根据误报估算结果将最弱的 p 值从列表中移除。其余具有统计显著性 p 值的要素在输出要素类中通过 Gi_Bin 或 COType 字段进行标识。虽然此方法并不完美,但经验检验显示此方法的效果好于假定各个局部测试是独立执行或应用传统的过于保守的多重测试方法。有关 FDR 校正的详细信息,请参见其他资源部分。
零假设和空间统计
“空间统计”工具箱中的几种统计工具都是推断式空间模式分析方法,其中包括空间自相关 (Global Moran's I)、聚类和异常值分析 (Anselin Local Moran's I) 和热点分析 (Getis-Ord Gi*)。推断统计都建立在概率论的基础之上。概率是对评测可能性的一种量度,它的基本原则是,所有的统计检验(直接或间接)都是概率计算,用于评估可能性在分析结果中的作用。通常,对于传统的(非空间)统计,您处理的是随机样本,并设法确定样本数据是否能够很好地代表(反映出)整个总体的概率。例如,您可能会问:“从投票站调查得出的结果(表明候选者 A 将以微弱优势打败候选者 B)反映出最终选举结果的几率有多大?”但是对于许多空间统计方法(包括上面列出的空间自相关类型统计),您通常处理的是研究区内的所有可用数据(所有犯罪案件、所有的疾病案例、所有人口普查区的属性等等)。在对整个总体计算统计数据时,得出的不再是估算值。您所掌握的是事实。因此,探讨可能性或概率不再有任何意义。那么,通常适用于研究区域中所有数据的空间模式分析工具如何才能合理地报告概率呢?答案就是,它们可以通过假设数据事实上是某个更大总体中的一部分(通过零假设)来实现这一点。请更细致地考虑这一点。
随机化零假设 - 在适当的情况下,“空间统计”工具箱中的工具会将随机化零假设作为统计显著性测试的基础。随机化零假设会假定对您的数据所观测到的空间模式表示的是多种 (n!) 可能的空间排列中的一种排列。如果您可以拾取数据值并将它们放置到研究区域中的各要素,则可能会得到这些值的某一种可能的空间排列。(请注意,拾取数据值并将它们任意放置是随机空间过程的一个示例)。随机化零假设表明的是,如果您可以无数次进行此练习(拾取数据,然后放置数据),则多数时候您所获得的模式与观测到的模式(真实数据)相比都没有明显差别。偶尔您可能会无意中将所有最高值放置到研究领域的同一角落中,但这样做的概率很小。随机化零假设表明的是,您的数据只是完全空间随机性的众多可能版本之一。数据值是固定不变的,只有它们的空间排列会发生变化。
归一化零假设 - 归一化零假设是一种常见的备选零假设,并不是由“空间统计”工具箱来执行。归一化零假设假定所观测到的值是通过某一随机抽样过程从无限大的呈正态分布的值总体中获得的。如果使用另一个样本,您会得到不同的值,但您仍期望这些值可以用来代表更大型的分布。归一化零假设表明的是,所获得的值代表了是众多可能的值样本之一。如果您能够将观测的数据与正态曲线拟合并从该分布中随机选择值来放置到研究区域,则多数时候您所获得的值模式和值分布与观测到的模板/分布(真实数据)相比都没有明显的差别。归一化零假设表明的是,您的数据及其排列是众多可能的随机样本之一。数据值及其空间排列都不是固定不变的。归一化零假设仅适用于数据值呈正态分布的情况。
其他资源
- Ebdon, David.Statistics in Geography, Blackwell, 1985.
- Mitchell, Andy.《ESRI GIS 分析手册(第 2 卷)》,ESRI 出版社,2005
- Goodchild, M.F., Spatial Autocorrelation,Catmog 47, Geo Books, 1986
- Caldas de Castro, Marcia, and Burton H. Singer."Controlling the False Discovery Rate:A New Application to Account for Multiple and Dependent Test in Local Statistics of Spatial Association."Geographical Analysis 38, pp 180-208, 2006.