Mit der Spatial Analyst-Lizenz verfügbar.
Der gelöste Stofftransport in einem porösen Medium umfasst zwei Hauptmechanismen: Advektion und hydrodynamische Dispersion. Die Advektion beschreibt den passiven Transport eines gelösten Stoffes mit der transportierenden Flüssigkeit. Dispersion ist die Vermischung des gelösten Stoffes mit der Flüssigkeit durch die differenzielle Bewegung der Flüssigkeiten durch Porenräume. Porous Puff geht davon aus, dass die grundwasserführende Schicht senkrecht gemischt ist. Das heißt, dass die Konzentration überall in einem vertikalen Abschnitt gleich ist. Dies ermöglicht die Anwendung eines mathematischen Modells in zwei Dimensionen, die von Seiten des Raster-Datenmodells erforderlich sind.
Zweidimensionale Dispersion
Die zweidimensionale Dispersion in einem porösen Medium wird von der Advektion-Dispersionsgleichung geregelt (Bear, 1979; Freeze und Cherry, 1979; und Marsily, 1986), die wie folgt in Bezug auf die Längs- (in der Fließrichtung) und Querrichtungen (senkrecht zur Fließrichtung) XL bzw. XT geschrieben wird:
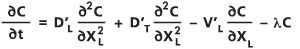
- Bedingung:
C: Die Konzentration des gelösten Stoffes als Funktion von zwei räumlichen Dimensionen und Zeit t.
∂C/∂t: Stellt die Zeitableitung dar.
D'L: Die effektiven (verlangsamten) Dispersionskoeffizienten in der Längsrichtung.
D'T: Die effektiven (verlangsamten) Dispersionskoeffizienten in der Querrichtung.
λ: Der Verfallskoeffizient, der als Konstante für exponentiellen Verfall der ersten Ordnung vorausgesetzt wird.
Dispersionskoeffizienten
Der Dispersionskoeffizient ist ein Maß der Ausdehnung, mit der sich der gelöste Stoff in der angegebenen Richtung ausbreitet:
D'I = DI/R
- Bedingung:
R: Der Retardationsfaktor.
i: Die Richtung (längs oder quer).
Der Dispersionskoeffizient bezieht sich auf das Verhalten des gelösten Stoffes in einem bestimmten Medium.
Beziehung zwischen Dispersivität und Dispersionskoeffizient
Die Dispersivitäten αL (Längsdispersivität) und αT (abgeleitet vom Dispersivitätsverhältnis) beziehen sich auf die Dispersionskoeffizienten:
D'L = αL V' und
D'T = αT V'
Wobei:
V': Die durchschnittliche verlangsamte Geschwindigkeit.
XL: Der Versatz in der Längsrichtung, parallel zur Fließrichtung im Massenzentrum.
XL: Der Versatz in der Querrichtung, senkrecht zur Fließrichtung im Massenzentrum.
V'L: Die verlangsamte gelöste Stoff-Geschwindigkeit in der Längsrichtung.
Im Grundwasserfluss:
V = q / n
- Bedingung:
q: Der Darcy-Durchfluss (Ablauf pro Querschnittfläche).
n: Die effektive Porosität der geologischen Formation.
V' = V / R
Eine ausführliche Erörterung der Transportgeschwindigkeiten finden Sie in der Dokumentation zu Darcy-Geschwindigkeit.
Gauß'sche Streuung
Die Näherungslösung zu dieser in Porous Puff verwendeten Gleichung basiert auf der Annahme der Gauß'schen Streuung einer unverzögerten Punktquelle in einer zweidimensionalen Domäne mit einer ursprünglichen Konzentration von Null (z. B. eine saubere, vertikal gemischte grundwasserführende Schicht) und wird von der folgenden Gleichung berechnet:
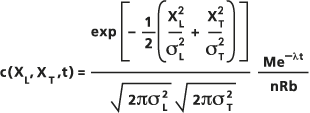
- Bedingung:
M: Die Masse des gelösten Stoffes, die unverzögert an der Quelle freigegeben wird, in Masseeinheiten.
n: Die Porosität der wasserführenden Schicht.
R: Der Retardationsfaktor.
b: Die Stärke der wasserführenden Schicht in Längeeinheiten.
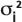 : Die Varianz der Gauß'schen Verteilung in den Längs- und Querrichtungen, bestimmt als eine Funktion der Längsdispersivität und des Dispersivitätsverhältnisses, die Sie angeben, und die Länge des Reisepfads vom Massemittelpunkt des von der Protokolldatei erhaltenen gelösten Stoffes.
: Die Varianz der Gauß'schen Verteilung in den Längs- und Querrichtungen, bestimmt als eine Funktion der Längsdispersivität und des Dispersivitätsverhältnisses, die Sie angeben, und die Länge des Reisepfads vom Massemittelpunkt des von der Protokolldatei erhaltenen gelösten Stoffes.
Die allgemeine elliptische Form dieser bivariaten Gauß'schen Verteilungsfunktion wird unten dargestellt:
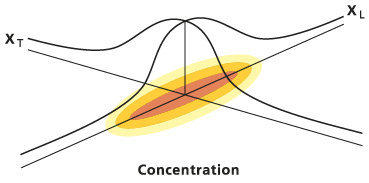
Es gibt mehrere wichtige Einschränkungen sowie in der Porous Puff-Lösung implizierte Annahmen. Die Dispersionsellipse wird in der Masse des gelösten Stoffes zentriert, von der angenommen wird, dass sie sich entlang der in der Eingabedatei beschriebenen Flussspur bewegt. Die Ausrichtung der Ellipse ist ebenfalls auf die Flussspur festgelegt, wobei die Hauptachse die Spur im Schwerpunkt tangiert. Die Porosität und die Stärke, die auch zur Verteilung beitragen, werden aus ihren jeweiligen Rastern am Schwerpunkt interpoliert und schließen keine Informationen von den umgebenden Zellen ein. Retardation, Zeit, Verfallskoeffizient, Längsdispersivität und Dispersivitätsverhältnis werden von Ihnen als Konstanten angegeben.
Dispersivität
Die Dispersivität ist ein Parameter, der die Dispersion eines gelösten Stoffes durch ein poröses Medium bestimmt, und der in Längeeinheiten angegeben wird. Im Porous Puff-Modell wird die Dispersivität verwendet, um die Varianz 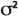 der oben aufgeführten Gauß'sche Streuungsgleichung zu berechnen, entsprechend:
der oben aufgeführten Gauß'sche Streuungsgleichung zu berechnen, entsprechend:
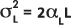 und
und 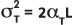
Die Art der Dispersivität und die Methoden für ihre Bestimmung sind Themen von großem Interesse und großer Kontroverse in der Gruppe der Personen, die sich mit der Grundwassermodellierung beschäftigen, und es gibt kein universell akzeptiertes Verfahren, ihre Werte zu schätzen. Eine Erörterung von Dispersivitäten in verschiedenen geologischen Formationen findet sich bei Gelhar et al. (1992).
Das folgende Diagramm fasst eine Vielzahl von Daten der veröffentlichten Literatur zusammen und verknüpft Längsdispersivität mit dem Maßstab des Problems von Interesse, in diesem Fall die Entfernung von der Quellenposition zum Punkt der Beobachtung.
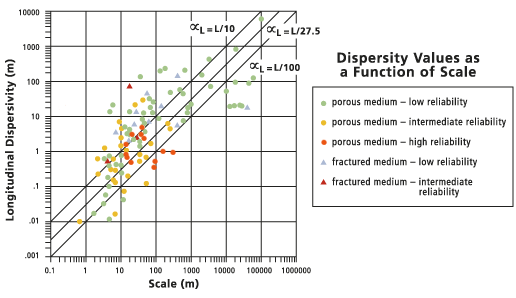
Die durchgezogene Linie (die Mittelachse) im Diagramm stellt den Standardwert für Längsdispersivität dar, der vom Werkzeug Porous Puff berechnet wird.
Die Linie wird durch eine linearen Regressionsanpassung von
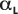 zu L erstellt, was zu
zu L erstellt, was zu 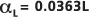 und das Beispiel
und das Beispiel 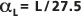 führt, wobei die Länge des Reisepfades L der Beobachtungsmaßstab ist.
führt, wobei die Länge des Reisepfades L der Beobachtungsmaßstab ist.Die Statistik dieser Regression wird ebenfalls angezeigt. Die gepunkteten äußeren Linien werden zum Vergleich an
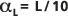 und
und 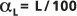 positioniert.
positioniert.
Diese Standardberechnung sollte nur als Anleitung verwendet werden, da einige Forscher die Verwendung so einer universellen Anpassung ablehnen. Bei jedem bestimmten Maßstab oder Standort variieren die gültigen Dispersivitäten möglicherweise über zwei Größenordnungen, wobei die zuverlässigeren Schätzungen zu den niedrigeren Werten tendieren. Statt den Standardwert zu verwenden, der keine theoretische Basis hat, sollten Sie mehrere Simulationen mithilfe eines Bereichs von Dispersivitäten ausführen. Dabei wird berücksichtigt, dass eine Reihe von Ergebnissen gültiger als das Verwenden der Ergebnisse einer einzelnen Simulation ist.
Ähnliche Vorbehalte gelten für die Schätzung des Verhältnisses von Längs- zu Querdispersivitäten, die in der folgenden Abbildung dargestellt werden. Diese Werte sind im Allgemeinen durch ein einfaches Verhältnis miteinander verknüpft, wobei Sie auch hier mit einem Wertebereich experimentieren sollten.
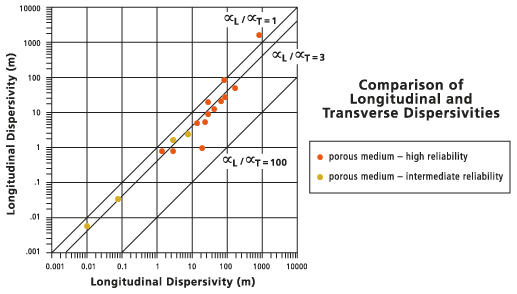
Das Standarddispersivitätsverhältnis 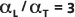 wird in der Abbildung unten durch die durchgezogene Linie (die Mittelachse) dargestellt. Die gepunkteten Linien (die äußeren Linien) werden zum Vergleich an
wird in der Abbildung unten durch die durchgezogene Linie (die Mittelachse) dargestellt. Die gepunkteten Linien (die äußeren Linien) werden zum Vergleich an 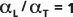 und
und 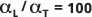 positioniert.
positioniert.
Gelhar et al. führen in der Aufstellung auch Werte für effektive Porosität und Transmissivität auf. Tabellen für diese Werte finden sich bei Freeze und Cherry (1979) und Marsily (1986).
Retardation
Retardation ist das Verhältnis zwischen der Geschwindigkeit der transportierenden Flüssigkeit und der des gelösten Stoffes und wird als Zahl zwischen eins und unendlich ausgedrückt, ohne Einheiten. Eine Retardation von zwei bedeutet, dass der gelöste Stoff mit der halben Sickergeschwindigkeit durch das poröse Medium migriert. Ein idealer Indikator durchläuft keine Adsorption und fließt in Lösung mit der Flüssigkeit. So ein gelöster Stoff hat eine Retardation von eins, was bedeutet, dass er sich mit der gleichen Rate wie die transportierende Flüssigkeit bewegt.
Dieses Phänomen ist das Ergebnis der Adsorption und Desorption des Bestandteils in der porösen Matrix, besonders in organische Schichten auf den Porenwänden. Die Retardationsgleichung wird in einer Erörterung von Freeze und Cherry (1979) wie folgt dargestellt:
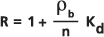
Bedingung:
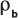 : Die Matrixmassendichte.
: Die Matrixmassendichte.n: Die Porosität der Formation.
K d: Der Verteilungskoeffizient, der die Partitionierung aufgrund einer schnellen, umkehrbaren Adsorption eines gelösten Stoffes zwischen flüssigen und festen Phasen darstellt, wobei eine lineare Isotherme angenommen wird.
Marsily (1986) erörtert ebenfalls ausführlich den Retardationsfaktor und die Adsorption.
Durchführen der Advektions-Dispersionsmodellierung
Die Werkzeuge Darcy-Strömung, Partikelverfolgung und Durchlässigkeit können verwendet werden, um rudimentäre Advektions-Dispersionsmodellierung von Grundwasserbestandteilen durchzuführen. Darcy-Strömung generiert ein Grundwasser-Fließgeschwindigkeitsfeld aus geologischen Daten, Partikelverfolgung folgt dem Weg der Advektion von einer Punktquelle durch das Fließfeld, und Durchlässigkeit berechnet die hydrodynamische Dispersion der unverzögerten punktuellen Freisetzung eines Bestandteils bei der Advektion am Fließpfad.
Eine vollständige Erörterung der Advektions-Dispersionsmodellierung mit diesen Werkzeugen wird bei Tauxe (1994) präsentiert.
Die typische Sequenz für die Grundwassermodellierung ist die Durchführung von Darcy-Strömung, Partikelverfolgung und dann Durchlässigkeit.
Beispiel
- Ein Beispiel für das Werkzeugdialogfeld von Porous Puff folgt:
Input particle track file : ttrack.txt
Input effective formation porosity raster: poros
Input saturated thickness raster: thickn
Ausgabe-Raster: ppuff1
Mass : 3.2e7
Dispersion time: 50000
Longitudinal dispersivity: 6
Dispersivity ratio: 3
Retardation factor: 1
Decay coefficient: 250
- Ein Beispiel für die Verwendung von Porous Puff in Map Algebra:
outPPuff1 = PorousPuff(ttrack.txt, poros, thickn, 1000000, 0.01, 10, 1.5, 1.0, 500)
- Eine Folge von Map Algebra-Ausdrücken mit der Suite der Grundwasser-Modellierungswerkzeuge folgt:
out_vol = DarcyFlow(head, poros, thickn, transm, dir1, mag1) ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, "#", "#", track_feat.shp) out_puff = PorousPuff(ttrack.txt, poros, thickn, 3.2e7, 50000, 6, 3, 1, 250)
Referenzliste
Bear, J. 1979, Hydraulics of Groundwater. McGraw–Hill.
Freeze, R. A. und J. A. Cherry. 1979. Groundwater. Prentice–Hall.
Gelhar, L. W., C. Welty und K. R. Rehfeldt. 1992. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research 28 (7): 1955–1974.
Marsily, G. de. 1986. Quantitative Hydrogeology. Academic Press.
Tauxe, J. D. 1994. "Porous Medium Advection–Dispersion Modeling in a Geographic Information System". Ph.D. diss., University of Texas, Austin.