Was ist Empirical Bayesian Kriging?

Mit der Geostatistical Analyst-Lizenz verfügbar.

Einführung

Empirical Bayesian Kriging (EBK) ist eine geostatistische Interpolationsmethode, die die schwierigsten Aspekte beim Erstellen eines gültigen Kriging-Modells automatisiert. Andere Kriging-Methoden in Geostatistical Analyst erfordern, dass Sie Parameter manuell anpassen, um präzise Ergebnisse zu erzielen, aber EBK berechnet diese Parameter automatisch durch einen Prozess von Teilmengenbildung und Simulationen.

Empirical Bayesian Kriging unterscheidet sich auch dadurch von anderen Kriging-Methoden, dass der Fehler berücksichtigt wird, der durch die Schätzung des zugrundeliegenden Semivariogramms entsteht. Andere Kriging-Methoden berechnen das Semivariogramm aus bekannten Datenpositionen und treffen anhand dieses einen Semivariogramms Vorhersagen für unbekannte Positionen. Dieser Prozess setzt implizit voraus, dass das geschätzte Semivariogramm das richtige Semivariogramm für die Interpolationsregion ist. Da sie die Unsicherheit der Semivariogramm-Schätzung nicht berücksichtigen, unterschätzen andere Kriging-Methoden die Standardfehler der Vorhersage.

Empirical Bayesian Kriging steht im Geostatistical Wizard und als Geoverarbeitungswerkzeug zur Verfügung.

Vor- und Nachteile

Vorteile

• Erfordert minimale interaktive Modellierung.
• Standardfehler der Vorhersage sind genauer als bei anderen Kriging-Methoden.
• Ermöglicht genaue Vorhersagen von mäßig nichtstationären Daten.
• Genauer als andere Kriging-Methoden für kleine Datasets.

Nachteile

• Verarbeitungsdauer erhöht sich rapide mit der steigenden Anzahl der Eingabepunkte, der Teilmengengröße oder dem Überlappungsfaktor. Durch Anwenden einer Transformation erhöht sich auch die Verarbeitungsdauer, insbesondere wenn K-Bessel oder K-Bessel Detrended als Semivariogramm-Modelltyp ausgewählt wird. Diese Parameter werden in den folgenden Abschnitten dieses Themas erläutert.
• Verarbeitung ist langsamer als bei anderen Kriging-Methoden, insbesondere bei der Ausgabe in Raster.
• Cokriging und anisotrope Korrekturen sind nicht verfügbar.
• Die Transformation "Log Empirical" ist besonders empfindlich gegenüber Ausreißern. Wenn Sie diese Transformation mit Daten verwenden, die Ausreißer enthalten, können Sie Vorhersagen erhalten, die um Größenordnungen größer oder kleiner als die Werte Ihrer Eingabepunkte sind. Dieser Parameter wird im Abschnitt "Transformationen" weiter unten beschrieben.

Schätzung von Semivariogrammen

Im Unterschied zu anderen Kriging-Methoden (die gewichtete Least-Squares verwenden) werden die Semivariogramm-Parameter in EBK mit dem Restricted Maximum Likelihood-Verfahren (REML) geschätzt. Wegen der Rechenbeschränkungen von REML für große Datasets werden die Eingabedaten zunächst in sich überlagernde Teilmengen einer bestimmten Größe (standardmäßig auf 100 Punkte pro Teilmenge) aufgeteilt. In jeder Teilmenge werden Semivariogramme auf folgende Weise geschätzt:

1. Ein Semivariogramm wird anhand der Daten in der Teilmenge geschätzt.
2. Mit diesem Semivariogramm als Modell werden an jeder Eingabeposition in der Teilmenge neue Daten ohne Bedingungen simuliert.
3. Ein neues Semivariogramm wird anhand der simulierten Daten geschätzt.
4. Die Schritte 2 und 3 werden so oft wiederholt wie angegeben. In jeder Wiederholung wird mithilfe des in Schritt 1 geschätzten Semivariogramms eine neue Gruppe von Daten an den Eingabepositionen simuliert und die simulierten Daten werden verwendet, um ein neues Semivariogramm zu schätzen.

Dieser Prozess erzeugt eine große Anzahl von Semivariogrammen für jede Teilmenge und wenn diese gemeinsam geplottet werden, ist das Ergebnis eine Verteilung von Semivariogrammen, die nach Dichte geschummert sind (je dunkler die blaue Farbe, desto mehr Semivariogramme verlaufen durch diese Region). Die empirischen Semivarianzen werden durch blaue Kreuze dargestellt. Zudem werden der Median der Verteilung mit einer durchgezogenen roten Linie und das 25. und 75. Perzentil durch rote gestrichelte Linien dargestellt, wie unten gezeigt.

Simulierte Semivariogramme

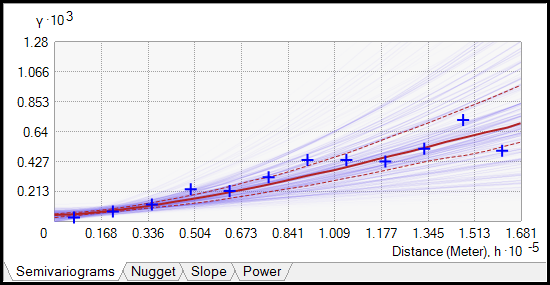
Die Anzahl simulierter Semivariogramme pro Teilmenge beträgt standardmäßig 100 und jedes dieser Semivariogramme ist eine Schätzung des wahren Semivariogramms für die Teilmenge.

Für jede vorhergesagte Position wird die Vorhersage anhand einer neuen Semivariogramm-Verteilung berechnet, die aus einer wahrscheinlichkeitsbasierten Referenzpunkterfassung einzelner Semivariogramme aus den Semivariogrammspektren in der Nachbarschaft des Punktes erzeugt wird. Wenn beispielsweise eine vorhergesagte Position in drei verschiedenen Teilmengen Nachbarn besitzt (wie durch die Suchnachbarschaft festgelegt) wird die Vorhersage mithilfe einiger simulierter Semivariogramme aus jeder der drei Teilmengen berechnet. Diese Semivariogramme werden probabilistisch basierend auf ihrer Wahrscheinlichkeitswerte ausgewählt.

Kriging-Modell

Empirical Bayesian Kriging unterscheidet sich von anderen Kriging-Methoden in Geostatistical Analyst, indem es eine intrinsische Zufallsfunktion als Kriging-Modell verwendet.

Andere Kriging-Modelle setzen voraus, dass der Prozess einem allgemeinen Durchschnitt (oder angegebenen Trend) mit einzelnen Variationen um diesen Durchschnitt folgt. Große Abweichungen werden zurück zum Durchschnitt gezogen, damit Werte nie zu stark abweichen. EBK setzt jedoch keine Tendenz zu einem allgemeinen Durchschnitt voraus, d. h., große Abweichungen können genauso wahrscheinlich größer wie kleiner werden. Infolgedessen sind intrinsische Zufallsfunktionen inhärent korrekt für Trends in den Daten.

Semivariogramm-Modell

Für eine gegebene Entfernung h unterstützt Empirical Bayesian Kriging die folgenden Semivariogramme:

• Potenz
  • γ(h)= Nugget + b|h|^α
• Linear
  • γ(h)= Nugget + b|h|
• Thin-Plate Spline
  • γ(h)= Nugget + b|h²|*ln(|h|)

Das Nugget und b (Neigung) müssen positiv sein und α (Potenz) muss zwischen 0,25 und 1,75 liegen. Unter diesen Beschränkungen werden die Parameter mithilfe von REML geschätzt. Diese Semivariogramm-Modelle haben keinen Bereich oder Sill-Parameter, da die Funktionen keine Obergrenze aufweisen.

In EBK ist es möglich, die empirische Verteilung der Parameterschätzungen zu analysieren, da an jeder Position viele Semivariogramme geschätzt werden. Durch Klicken auf die Registerkarte Nugget, Neigung oder Potenz werden die Verteilungen der jeweiligen Parameter angezeigt. Die folgende Grafik zeigt die Verteilungen der Semivariogramm-Parameter für die simulierten Semivariogramme aus der vorherigen Grafik:

Verteilungen von Nugget, Neigung und Potenz

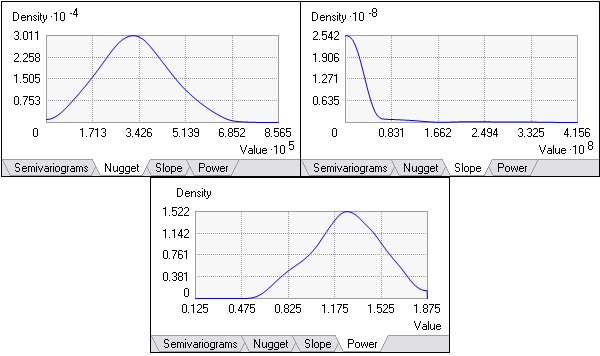
Wenn Sie in der Vorschau-Oberfläche auf eine andere Position klicken, werden die Semivariogramm-Verteilung und die Verteilungen der Semivariogramm-Parameter für die neue Position angezeigt. Wenn sich die Verteilungen über die Datendomäne nicht signifikant ändern, lässt sich darauf schließen, dass die Daten global stationär sind. Die Verteilungen sollten sich gleichmäßig über die Datendomäne ändern. Wenn Sie jedoch große Veränderungen in den Verteilungen über kleine Entfernungen entdecken, können die Übergänge der Verteilungen durch die Angabe eines höheren Wertes für Überlappungsfaktor geglättet werden.

Hinweis:

Wie im nachfolgenden Abschnitt "Transformationen" beschrieben, verwandelt das Anwenden einer Transformation das Kriging-Modell von einer intrinsischen Zufallsfunktion in ein einfaches Kriging-Modell und mehrere zusätzliche Semivariogramm-Modelle werden verfügbar.

Transformationen

Empirical Bayesian Kriging bietet die Normalverteilungstransformation mit "Multiplicative Skewing" und der Option für zwei Basisverteilungen: "Empirical" und "Log Empirical". Die Transformation "Log Empirical" erfordert, dass alle Datenwerte positiv sind, und garantiert, dass alle Vorhersagen positiv sind. Dies eignet sich für Daten wie Niederschlag, die nicht negativ sein können.

Transformationsoptionen

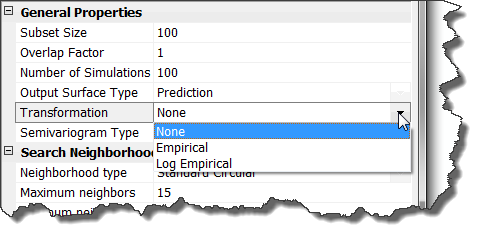
Wenn eine Transformation angewendet wird, wird ein Simple Kriging-Modell anstelle einer intrinsischen Zufallsfunktion verwendet. Aufgrund dieser Änderungen ändern sich die Parameterverteilungen zu Nugget, Partial Sill und Range.

Wenn K-Bessel oder K-Bessel Detrended als Semivariogrammtyp ausgewählt wird, wird ein zusätzliches Diagramm für den Parameter Shape in K-Bessel angezeigt. Außerdem wird die zusätzliche Registerkarte Transformation eingeblendet, die die Verteilung der angepassten Transformationen (eine pro Simulation) anzeigt. Wie auf der Registerkarte Semivariogramme ist die Transformationsverteilung nach Dichte gefärbt und Quantillinien werden dargestellt.

Verteilungen von Nugget, Partial Sill, Range und Transformation

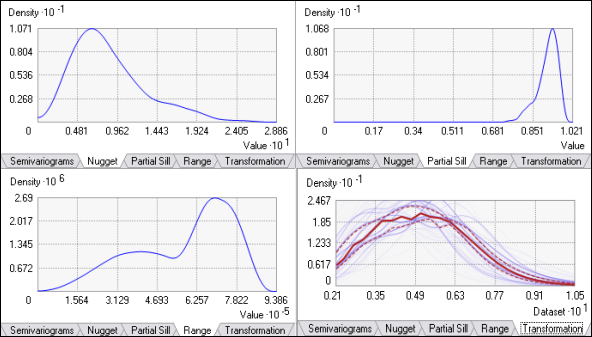
Semivariogramme

Alle geostatistischen Methoden setzen räumliche Autokorrelation voraus, d. h., näher gelegene Elemente sind ähnlicher als weiter entfernte und das Semivariogramm definiert, wie sich diese Ähnlichkeit mit größerer Entfernung verringert. Einige Semivariogramme (z. B. Exponential) setzen voraus, dass sich die Ähnlichkeit rasch verringert. Das Whittle-Semivariogramm-Modell setzt hingegen voraus, dass sich die Ähnlichkeit langsam verringert. Selbst mit denselben Nugget, Range und Sill definieren diese beiden Semivariogramme die sich verringernde Ähnlichkeit auf sehr unterschiedliche Weise. Der Schlüssel für zuverlässige Ergebnisse liegt in der Auswahl des Semivariogramms, das dem Verhalten des betreffenden Phänomens am besten entspricht. Die verfügbaren Semivariogramm-Modelle hängen von der Wahl der Transformation ab.

Wenn die Transformation auf Keine eingestellt ist, sind die folgenden Semivariogramm-Modelle verfügbar:

• Potenz (Standard)
• Linear
• Thin-Plate Spline

Wenn die Transformation auf Empirical oder Log Empirical eingestellt ist, sind die folgenden Semivariogramm-Modelle verfügbar:

• Exponential (Standard)
• Exponential Detrended
• Whittle
• Whittle Detrended
• K-Bessel
• K-Bessel Detrended

Die drei Detrended-Semivariogramm-Modelle sind identisch mit ihren Nicht-Detrended-Entsprechungen mit der Ausnahme, dass eine Trendentfernung der ersten Ordnung angewendet wird. Das Entfernen von Trends hat einen vernachlässigbaren Einfluss auf die Rechengeschwindigkeit. Das Vorhandensein von Trends lässt sich mit dem Werkzeug "Trend Analysis ESDA" prüfen.

Vor- und Nachteile der einzelnen Modelle

Bei jedem Semivariogramm gibt es Vor- und Nachteile. Wenn Sie ein Semivariogramm auswählen, sollten Sie die Rechendauer und die Flexibilität des Modells (die Fähigkeit, ein breites Spektrum an Datasets einzubeziehen) berücksichtigen:

• Potenz
  • Vorteile: relativ schnell und flexibel. Generell eine gute Wahl, bei der sich Performance und Genauigkeit die Waage halten.
  • Nachteile: weniger flexibel und langsamer als andere Optionen.
• Linear
  • Vorteile: sehr schnell.
  • Nachteile: am wenigsten flexibles Modell.
• Thin-Plate Spline
  • Vorteile: sehr schnell. Funktioniert am besten, wenn starke Trends vorhanden sind.
  • Nachteile: weniger flexibel, insbesondere wenn kein Trend vorhanden ist.
• Exponential
  • Vorteile: bietet eine flexible Transformation. Schneller als K-Bessel und K-Bessel Detrended.
  • Nachteile: Form des Semivariogramms ist nicht flexibel. Langsam im Vergleich zu "Potenz", "Linear" und "Thin-Plate Spline".
• Exponential Detrended
  • Vorteile: bietet eine flexible Transformation. Schneller als K-Bessel und K-Bessel Detrended. Entfernt Trend der ersten Ordnung.
  • Nachteile: Form des Semivariogramms ist nicht flexibel. Langsam im Vergleich zu "Potenz", "Linear" und "Thin-Plate Spline".
• Whittle
  • Vorteile: bietet eine flexible Transformation. Schneller als K-Bessel und K-Bessel Detrended.
  • Nachteile: Form des Semivariogramms ist nicht flexibel. Langsam im Vergleich zu "Potenz", "Linear" und "Thin-Plate Spline".
• Whittle Detrended
  • Vorteile: bietet eine flexible Transformation. Schneller als K-Bessel und K-Bessel Detrended. Entfernt Trend der ersten Ordnung.
  • Nachteile: Form des Semivariogramms ist nicht flexibel. Langsam im Vergleich zu "Potenz", "Linear" und "Thin-Plate Spline".
• K-Bessel
  • Vorteile: am flexibelsten und genauesten.
  • Nachteile: Berechnung dauert am längsten.
• K-Bessel Detrended
  • Vorteile: am flexibelsten und genauesten. Entfernt Trend der ersten Ordnung.
  • Nachteile: Berechnung dauert am längsten.

Auswählen eines Semivariogramms

Die Auswahl des Semivariogramms sollte meistens anhand der folgenden Kriterien kein Problem darstellen:

• Wenn Sie bereit sind zu warten, um die besten Ergebnisse zu erhalten, sollte "K-Bessel" oder "K-Bessel Detrended" ausgewählt werden. Die Tatsache, ob ein Trend vorhanden ist oder nicht, sollte die Auswahl bestimmen.
• Wenn Sie schnell Ergebnisse benötigen und dafür etwas Genauigkeit opfern möchten, sollten Sie "Linear" oder "Thin-Plate Spline" auswählen. Wenn kein Trend oder nur ein schwacher Trend vorhanden ist, ist "Linear" die bessere Option.
• Falls Sie ein Optimum von Genauigkeit und Geschwindigkeit benötigen, empfiehlt sich die Option "Potenz".
• Wenn eine Transformation erforderlich ist, Sie aber nicht lange auf die Ausgabe warten können, sollte "Exponential" oder "Whittle" (oder deren Detrended-Entsprechung) ausgewählt werden. Sie sollten die Transformation auswählen, die den empirischen Semivarianzen im Geostatistical Wizard (unten beschrieben) am besten entsprechen. Kreuzvalidierung sollte ebenfalls in Erwägung gezogen werden.

Wenn Sie sich zwischen "Exponential", "Whittle" und ihren Detrended-Entsprechungen entscheiden wollen, sollten Sie das Semivariogramm auswählen, das visuell am besten zu den empirischen Semivarianzen passt (die blauen Kreuze in der folgenden Grafik). Idealerweise sollten die empirischen Semivarianzen in die Mitte des Semivariogrammspektrums fallen. Beispielsweise fallen die blauen Kreuze in der folgenden Grafik nicht in die Mitte des Semivariogrammspektrums (die meisten fallen in die Richtung des oberen Spektrums):

Empirische Semivarianzen fallen nicht in die Mitte des Spektrums.

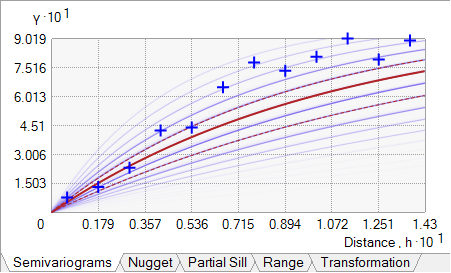
Stattdessen sollte das folgende Semivariogramm bevorzugt werden, da die blauen Kreuze in die Mitte des Semivariogrammspektrums fallen:

Empirische Semivarianzen fallen in die Mitte des Spektrums.

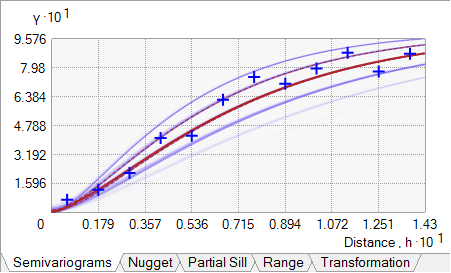
Entfernungsberechnungen für Daten in geographischen Koordinaten

Wenn sich Ihre Eingabedaten in einem geographischen Koordinatensystem befinden, werden Entfernungen anhand der Sehnenentfernung berechnet. Die Sehnenentfernung zwischen zwei beliebigen Punkten ist die gerade Linie, die die Punkte verbindet. Diese Linie verläuft durch die Erde und nicht entlang ihrer Oberfläche. Um dies zu veranschaulichen, stellen Sie sich einen Lichtstrahl durch eine transparente Kugel vor. Die Länge des Lichtstrahls zwischen dem Punkt, an dem das Licht in die Kugel eintritt, und dem Punkt, an dem es aus der Kugel austritt, ist die Sehnenentfernung zwischen diesen beiden Punkten. Der primäre Vorteil der Verwendung der Sehnenentfernung anstelle der geodätischen Entfernung besteht darin, dass es weniger rechenintensiv ist. Außerdem gibt es nur begrenzt Theorien über das Ausführen von Kriging an Sphäroiden.

Hinweis:

Da die Sehnenentfernungen keine guten Annäherungen von geodätischen Entfernungen über mehr als 30 Dezimalgrad bieten, darf der Suchradius 15 Dezimalgrad nicht überschreiten (d. h., der Durchmesser kann 30 Grad nicht überschreiten) und jede Position, die innerhalb von 15 Dezimalgrad keine Nachbarn hat, wird als NoData berechnet. Zusätzlich erfordern einige Semivariogramm-Modelle das Anpassen einer flachen Ebene an jede Teilmenge, um das Entfernen von Trends auszuführen. Diese Ebene lässt sich nicht genau für Teilmengen erstellen, deren Ausdehnung 30 Dezimalgrad überschreitet, daher ist die Ausdehnung einzelner Teilmengen für die folgenden Semivariogramm-Modelle auf 30 Grad beschränkt:

• Thin-Plate Spline
• Exponential Detrended
• Whittle Detrended
• K-Bessel Detrended

In früheren Versionen von ArcGIS wurden geographische Koordinaten als Quadratkoordinaten behandelt und zwischen den Punkten wurde die euklidische Entfernung berechnet. Eine Zelle mit der Größe ein Grad mal ein Grad ist jedoch nicht wirklich ein Quadrat, deshalb wird diese Entfernung verzerrt. Diese Verzerrung wird stärker, je weiter Sie sich vom Äquator aus nach Norden oder Süden bewegen.

Zusätzliche Parameter für Empirical Bayesian Kriging

Empirical Bayesian Kriging nutzt drei Parameter, die nicht in anderen Kriging-Methoden vorhanden sind:

• Subset Size–Gibt die Anzahl der Punkte in jeder Teilmenge an. Je größer die Teilmengengröße, desto länger braucht EBK für die Berechnung.
• Überlappungsfaktor–Gibt den Grad der Überlappung zwischen Teilmengen an. Jeder Eingabepunkt kann in mehreren Teilmengen liegen. Der Überlappungsfaktor gibt die durchschnittliche Anzahl von Teilmengen an, in denen jeder Punkt liegt. Beispielsweise bedeutet ein Überlappungsfaktor von 1,5, dass ungefähr die Hälfte der Punkte in einer Teilmenge und die andere Hälfte in zwei Teilmengen verwendet wird. Ein höherer Wert für den Überlappungsfaktor führt zu einer glatteren Ausgabe-Oberfläche, er erhöht jedoch auch die Verarbeitungszeit.
• Number of Simulations–Gibt die Anzahl der Semivariogramme an, die für jede Teilmenge simuliert werden. Mehr Simulationen führen zu genaueren Vorhersagen, aber die Verarbeitungsdauer erhöht sich ebenfalls.

Referenzen

• Chilès, J-P., und P. Delfiner (1999). Kapitel 4 von Geostatistics: Modeling Spatial Uncertainty. New York: John Wiley & Sons, Inc.
• Krivoruchko K. (2012). "Empirical Bayesian Kriging", ArcUser Fall 2012.
• Krivoruchko K. (2012). "Modeling Contamination Using Empirical Bayesian Kriging," ArcUser Fall 2012.
• Krivoruchko K. und Gribov A. (2014). "Pragmatic Bayesian kriging for non-stationary and moderately non-Gaussian data", Mathematics of Planet Earth. Proceedings of the 15^th Annual Conference of the International Association for Mathematical Geosciences. Springer 2014, pp. 61-64.
• Pilz, J., und G. Spöck (2007). "Why Do We Need and How Should We Implement Bayesian Kriging Methods", Stochastic Environmental Research and Risk Assessment 22 (5): 621–632.