Mit dem Werkzeug Clustering von hohen/niedrigen Werten wird die Konzentration von hohen oder niedrigen Werten für eine angegebenes Untersuchungsgebiet gemessen.
Berechnungen

Anzeigen zusätzlicher General G-Statistikberechnungen.
Beachten Sie, dass der einzige Unterschied zwischen Zähler und Nenner die Gewichtung (wij) ist. Clustering von hohen/niedrigen Werten funktioniert nur mit positiven Werten. Demzufolge liegt der Bereich für General G zwischen 0 und 1, wenn die Gewichtungen binär (0/1) oder immer kleiner als 1 sind. Ein Schema mit binärer Gewichtung wird für diese Statistik empfohlen. Wählen Sie "Festes Entfernungsband", "Polygonnachbarschaft", "Nächste Nachbarn (K)" oder Delaunay Triangulation für den Parameter Konzeptualisierung von räumlichen Beziehungen aus. Wählen Sie "Keine" für den Parameter Standardisierung aus.
Interpretation
Das Werkzeug Clustering von hohen/niedrigen Werten (Getis-Ord General G) ist eine schlussfolgernde Statistik, d. h. die Ergebnisse der Analyse im Kontext der Null-Hypothese werden interpretiert. Die Null-Hypothese für die Statistik der Cluster-Bildung von hohen oder niedrigen Werten (General G) gibt an, dass kein räumliches Clustering von Feature-Werten vorhanden ist. Wenn der von diesem Werkzeug zurückgegebene p-Wert klein und statistisch signifikant ist, kann die Null-Hypothese abgelehnt werden (siehe Was ist ein Z-Wert? Was ist ein p-Wert?). Wenn die Null-Hypothese abgelehnt wird, ist der Z-Wert wichtig. Wenn der Z-Wert positiv ist, ist der beobachtete General G-Index größer als der erwartete General G-Index, was darauf hinweist, dass hohe Werte für das Attribut im Untersuchungsgebiet geclustert werden. Wenn der Z-Wert negativ ist, ist der beobachtete General G-Index kleiner als der erwartete Index, wodurch angegeben wird, dass niedrige Werte im Untersuchungsgebiet geclustert werden.
Das Werkzeug Clustering von hohen/niedrigen Werten (Getis-Ord General G) ist am besten geeignet, wenn eine relativ gleichmäßige Verteilung von Werten vorliegt und Sie nach unerwarteten räumlichen Spitzen mit hohen Werten suchen. Wenn hohe und niedrige Werte Cluster bilden, tendieren sie leider dazu, sich gegenseitig aufzuheben. Um die räumliche Cluster-Bildung zu messen, wenn sowohl hohe als auch niedrige Werte Cluster bilden, verwenden Sie das Werkzeug Räumliche Autokorrelation.
Die Null-Hypothese für die Werkzeuge Clustering von hohen/niedrigen Werten (Getis-Ord General G) und Räumliche Autokorrelation (Morans I) ist zufällige räumliche Verteilung (Complete Spatial Randomness, CSR); Werte werden nach dem Zufallsprinzip auf die Features im Dataset verteilt, wodurch zufällige räumliche Prozesse bei der Arbeit dargestellt werden. Die Interpretation von Z-Werten für das Werkzeug "Clustering von hohen/niedrigen Werten" unterscheidet sich deutlich von der Interpretation der Z-Werte für das Werkzeug "Räumliche Autokorrelation (Morans I)":
| Ergebnis | Clustering von hohen/niedrigen Werten (Getis-Ord General G) | Räumliche Autokorrelation |
|---|---|---|
Der p-Wert ist nicht statistisch signifikant. | Die Null-Hypothese kann nicht abgelehnt werden. Es ist gut möglich, dass die räumliche Verteilung der Feature-Attributwerte das Ergebnis zufälliger räumlicher Prozesse ist. Anders ausgedrückt, könnte das beobachtete räumliche Muster von Werten eine von vielen, vielen möglichen Versionen der zufälligen räumlichen Verteilung sein. | |
Der p-Wert ist statistisch signifikant und der Z-Wert ist positiv. | Die Null-Hypothese kann abgelehnt werden. Die räumliche Verteilung von hohen Werten im Dataset weist mehr räumliche Gruppierungen auf als erwartet würden, wenn die unterliegenden räumlichen Prozesse tatsächlich zufällig wären. | Die Null-Hypothese kann abgelehnt werden. Die räumliche Verteilung von hohen Werten und/oder niedrigen Werten im Dataset weist mehr räumliche Gruppierungen auf als erwartet würden, wenn die unterliegenden räumlichen Prozesse tatsächlich zufällig wären. |
Der p-Wert ist statistisch signifikant und der Z-Wert ist negativ. | Die Null-Hypothese kann abgelehnt werden. Die räumliche Verteilung von niedrigen Werten im Dataset weist mehr räumliche Gruppierungen auf als erwartet würden, wenn die unterliegenden räumlichen Prozesse tatsächlich zufällig wären. | Die Null-Hypothese kann abgelehnt werden. Die räumliche Verteilung von hohen und niedrigen Werten im Dataset weist eine räumlichere Verteilung auf als erwartet würde, wenn die unterliegenden räumlichen Prozesse tatsächlich zufällig wären. Ein verteiltes räumliches Muster gibt häufig eine Art von Mitbewerbsprozess wieder: ein Feature mit hohen Werten lehnt andere Features mit hohen Werten häufig ab; entsprechend lehnt ein Feature mit einem niedrigen Wert andere Features mit niedrigen Werten ab. |
Ausgabe
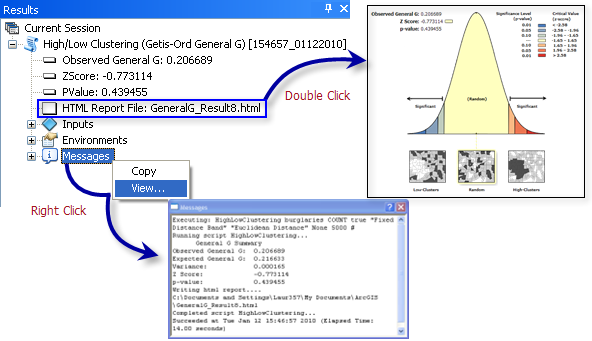
Das Werkzeug "Clustering von hohen/niedrigen Werten" gibt vier Werte zurück: beobachteter General G-Index, erwarteter General G-Index, Z-Wert und p-Wert. Auf diese Werte kann im Fenster Ergebnisse zugegriffen werden. Sie können auch als abgeleitete Ausgabewerte zur möglichen Verwendung in Modellen oder Skripten übergeben werden. Optional erstellt dieses Werkzeug eine HTML-Datei mit einer grafischen Zusammenfassung der Ergebnisse. Wenn Sie im Fenster Ergebnisse auf die HTML-Datei doppelklicken, wird die HTML-Datei im standardmäßigen Internetbrowser geöffnet. Wenn Sie im Fenster Ergebnisse mit der rechten Maustaste auf den Eintrag "Meldungen" klicken und "Anzeigen" auswählen, werden die Ergebnisse in einem Meldungsdialogfeld angezeigt.
Häufig gestellte Fragen
F: Ergebnisse des Werkzeugs Hot-Spot-Analyse (Getis-Ord Gi*) geben statistisch signifikante Hot-Spots an. Warum sind die Ergebnisse des Werkzeugs "Clustering von hohen/niedrigen Werten (Getis-Ord General G)" nicht auch statistisch signifikant?
A: Globale Statistiken wie das Werkzeug Clustering von hohen/niedrigen Werten (Getis-Ord General G) bewerten das Muster und den Trend der Daten insgesamt. Sie sind am effektivsten, wenn das räumliche Muster im gesamten Untersuchungsgebiet konsistent ist. Lokale Statistikwerkzeuge (wie Hot-Spot-Analyse) bewerten jedes Feature im Kontext benachbarter Features und vergleichen die lokale Situation mit der globalen Situation. Sehen Sie sich das folgende Beispiel an. Wenn Sie einen Mittelwert oder Durchschnitt für eine Gruppe von Werten berechnen, wird gleichzeitig eine globale Statistik berechnet. Wenn alle Werte nahe 20 liegen, liegt der Mittelwert ebenfalls nahe 20, wobei dieses Ergebnis insgesamt eine sehr gute Repräsentation/Zusammenfassung des Datasets ist. Wenn die eine Hälfte der Werte jedoch nahe 1 und die andere Hälfte der Werte nahe 100 liegt, liegt der Mittelwert nahe 50. Da möglicherweise keine Datenwerte nahe 50 vorhanden sind, ist der Mittelwert insgesamt keine gute Repräsentation/Zusammenfassung des Datasets. Wenn Sie ein Histogramm der Datenwerte erstellen, wird jedoch die bimodale Verteilung angezeigt. Entsprechend sind globale räumliche Statistiken, einschließlich des Werkzeugs "Clustering von hohen/niedrigen Werten" am effektivsten, wenn die gemessenen räumlichen Prozesse im gesamten Untersuchungsgebiet konsistent sind. Die Ergebnisse sind dann eine gute Repräsentation/Zusammenfassung des räumlichen Musters insgesamt. Weitere Informationen und die Analyse der dargestellten SIDs finden Sie in den unten aufgeführten Quellen zu Getis und Ord (1992).
F: Warum unterscheiden sich die Ergebnisse des Werkzeugs Clustering von hohen/niedrigen Werten (Getis-Ord General G) von den Ergebnissen des Werkzeugs Räumliche Autokorrelation (Morans I)?
A: Weitere Informationen finden Sie in der Tabelle oben. Diese Werkzeuge messen unterschiedliche räumliche Muster.
F: Können Sie die Z-Werte bzw. p-Werte dieses Werkzeugs mit den Ergebnissen einer Analyse eines anderen Untersuchungsgebiets vergleichen?
A: Ergebnisse können eigentlich nicht verglichen werden, es sei denn, das Untersuchungsgebiet und die Parameter, die für die Analyse herangezogen wurden, sind festgelegt (für alle Analysen, die Sie vergleichen möchten identisch). Wenn das Untersuchungsgebiet jedoch einen festgelegten Polygonsatz umfasst und die Analyseparameter festgelegt sind, können Sie Z-Werte für ein bestimmtes Attribut im Zeitverlauf vergleichen. Angenommen, Sie möchten Trends bei der Cluster-Bildung von Käufen nicht verschreibungspflichtiger Medikamente auf Bezirksebene für einen bestimmten Kreis analysieren. Sie können Clustering von hohen/niedrigen Werten für jeden Zeitraum ausführen und anschließend ein Liniendiagramm der Ergebnisse erstellen. Wenn sich herausstellt, dass die Z-Werte statistisch signifikant sind und steigen, können Sie daraus schließen, dass die Intensität von räumlichem Clustering für hohe Werte bei Käufen nicht verschreibungspflichtiger Medikamente steigt.
F: Hat die Feature-Größe Auswirkungen auf die Analyse?
A: Die Größe der Features kann Auswirkungen auf die Ergebnisse haben. Wenn die großen Polygone beispielsweise zu niedrigen Werten und die kleineren Polygone zu hohen Werten neigen, obwohl die Konzentration von hohen und niedrigen Werten gleich ist, kann der beobachtete General G-Index höher sein als der erwartete General G-Index, da sich innerhalb der angegebenen Entfernung mehrere Paare kleinerer Polygone befinden.
Potenzielle Anwendungsbereiche
- Ermitteln unerwarteter Spitzen bei der Anzahl von Besuchen in der Notfallaufnahme, die auf den Ausbruch eines lokalen oder regionalen Gesundheitsproblems hinweisen können.
- Vergleichen des räumlichen Musters verschiedener Einzelhandelstypen in einer Stadt, um zu ermitteln, welche Typen mit Wettbewerb gruppiert werden, um Preisvergleiche zu nutzen (beispielsweise Autohändler), und welche Typen Wettbewerb ablehnen (beispielsweise Fitnesscenter).
- Zusammenfassen der Cluster-Stufe räumlicher Phänomene, um Änderungen zu verschiedenen Zeiten oder an verschiedenen Orten zu überprüfen. Es ist beispielsweise bekannt, dass Städte und deren Bevölkerungen Cluster bilden. Mit der Analyse von hohen/niedrigen Werten können Sie die Cluster-Stufe von Bevölkerungen in einer Stadt im Zeitverlauf vergleichen (Analyse von Städtewachstum und Bevölkerungsdichte).
Zusätzliche Quellen
Getis, Arthur, and J. K. Ord. "The Analysis of Spatial Association by Use of Distance Statistics." Geographical Analysis 24, no. 3. 1992.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.