Raster-Daten entstehen im Allgemeinen beim Scannen von Karten oder Erfassen von Luft- und Satellitenbildern. Datasets von gescannten Karten enthalten normalerweise keine räumlichen Referenzdaten, die in die Datei eingebettet sind oder extern vorliegen. Bei Luft- und Satellitenbildern ist die mitgelieferte Positionsgenauigkeit oft unzureichend, sodass die Daten nicht mit bereits vorhandenen Daten deckungsgleich sind. Damit Raster-Datasets in Verbindung mit anderen räumlichen Daten verwendet werden können, muss möglicherweise eine Anpassung oder eine geographische Referenzierung an das Kartenkoordinationssystem vorgenommen werden. Ein Kartenkoordinatensystem wird über eine Kartenprojektion (eine Methode zur Abbildung der gebogenen Erdoberfläche auf eine Ebene) definiert.
Wenn Sie die Raster-Daten geographisch referenzieren, definieren Sie die Lage anhand von Kartenkoordinaten und weisen das Koordinatensystem des Datenrahmens zu. Die Georeferenzierung von Raster-Daten ermöglicht, diese Daten zusammen mit anderen geographischen Daten anzuzeigen, abzufragen und zu analysieren. Mit der Werkzeugleiste Georeferenzierung können Sie Raster-Datasets, Raster-Layer (die möglicherweise über Raster-Funktionen verfügen), Image-Services und Raster-Produkte georeferenzieren.
Bei der geographischen Referenzierung eines Rasters werden im Allgemeinen drei Schritte ausgeführt:
- Fügen Sie in ArcMap das Raster hinzu, das Sie an den projizierten Daten ausrichten möchten.
- Fügen Sie Links hinzu, die bekannte Positionen des Raster-Datasets mit bekannten Positionen in Kartenkoordinaten verbinden. Mit dem Werkzeug Automatische Registrierung
 können Sie Links automatisch erstellen.
können Sie Links automatisch erstellen. - Speichern Sie die Informationen zur geographischen Referenzierung, wenn Sie mit der Anpassung zufrieden sind.
Ausrichten des Rasters an Passpunkten
Im Allgemeinen richten Sie bei der Georeferenzierung die Raster-Daten an vorhandenen räumlichen Daten (Zieldaten) aus, z. B. an georeferenzierten Rastern oder einer Feature-Class für Vektoren, die sich im gewünschten Karten-Koordinatensystem befindet. Es müssen also mehrere Passpunkte auf der Erdoberfläche festgelegt werden, deren Lagekoordinaten bekannt sind. Diese Positionen müssen sowohl im Raster-Dataset als auch in den Raumbezugsdaten (Zieldaten) vorhanden sein. Passpunkte sind Positionen, die sowohl im Raster-Dataset als auch in realen Koordinaten bestimmt werden können. Als identifizierbare Positionen können viele verschiedene Feature-Typen verwendet werden, beispielsweise Straßenkreuzungen, das Delta eines Flusslaufs, Höhenrücken, das Ende einer Landzunge, die Ecke eines Feldes, Straßenecken oder die Überschneidung zweier Heckenreihen.
Die Passpunkte werden verwendet, um eine Polynomtransformation zu erstellen, die das Raster-Dataset von der Ursprungsposition in die räumlich korrekten Koordinaten ändert. Die Verbindung eines Passpunktes im Raster-Dataset (Ausgangspunkt) mit dem entsprechenden Punkt in den Zieldaten (Zielpunkt) wird als Link bezeichnet.
In der folgenden Abbildung ist ein Passpunkt (gelbes Kreuz) über den Vektorzieldaten an einer Straßenkreuzung positioniert, der zugeordnete Passpunkt (grünes Kreuz) über dem Raster-Dataset. Der entsprechende Link wird durch die blaue Verbindungslinie zwischen den beiden Passpunkten dargestellt.
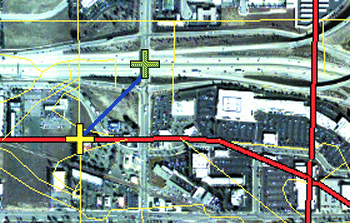
Die Anzahl der zu erstellenden Links hängt von der Komplexität der Transformation ab, mit der Sie das Raster-Dataset in Kartenkoordinaten transformieren möchten. Das Einfügen von mehr Links führt nicht automatisch zu einer besseren Registrierung. Wenn möglich, sollten Sie die Links über das gesamte Raster-Dataset verteilen und sie nicht in einem Bereich konzentrieren. Ein Link in der Nähe jeder Ecke des Raster-Datasets und einige Links, über die Fläche verteilt, reichen, um ein gutes Ergebnis zu erzielen.
In der Regel ist das Ergebnis bei der Einpassung besser, je mehr Überlappungen zwischen dem Raster-Dataset und den Zieldaten vorliegen. Die Punkte, mit denen das Raster-Dataset geographisch referenziert wird, sind so breiter gestreut. Beispiel: Wenn die Zieldaten nur ein Viertel der Fläche des Raster-Datasets ausmachen, wären die Punkte, an denen das Raster-Dataset ausgerichtet werden könnte, auf die Fläche der Überlappung beschränkt. Die Bereiche außerhalb der Überlappung werden also vermutlich nicht korrekt transformiert.
Bedenken Sie stets, dass georeferenzierte Daten nur so gut sein können wie die verwendeten Transformationsparameter. Um Fehler möglichst zu vermeiden, sollten Sie als Ziel für die Georeferenzierung Daten in der höchstmöglichen Auflösung und mit dem größten zu verwendenden Maßstab wählen.
Transformieren des Rasters
Wenn Sie genügend Links erstellt haben, können Sie das Raster-Dataset dauerhaft in Kartenkoordinaten der Zieldaten transformieren. Die korrekten Positionen der Kartenkoordinaten aller Zellen im Raster können Sie mit einer Polynom-, Spline-, Anpassungs-, Projektiv- oder Ähnlichkeitstransformation bestimmen.
Bei der Polynomtransformation wird ein Polynom verwendet, das auf Grundlage der Passpunkte und eines Algorithmus zur Anpassung mit der Methode der kleinsten Quadrate (LSF) berechnet wird. Das Polynom ist für globale Genauigkeit optimiert, kann jedoch keine lokale Genauigkeit garantieren. Bei der Polynomtransformation werden zwei Formeln verwendet: eine zur Berechnung der X-Koordinate (Ausgabe) und eine zur Berechnung der Y-Koordinate für eine XY-Position (Eingabe). Das Ziel des Algorithmus der kleinsten Quadrate besteht darin, eine allgemeine Formel abzuleiten, die auf alle Punkte angewendet werden kann, für gewöhnlich aber unter geringer Verschiebung der Positionen der Passpunkte. Die Anzahl der für diese Methode erforderlichen nicht korrelierten Passpunkte beträgt eins für die Transformation der Ordnung 0, drei für die affine Transformation erster Ordnung, sechs für die zweite Ordnung und zehn für die dritte Ordnung. Bei Polynomen niedrigerer Ordnung wird meistens ein Zufallsfehler und bei Polynomen höherer Ordnung meistens ein Extrapolationsfehler ausgegeben.
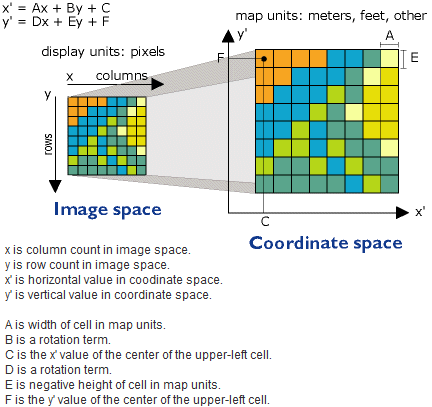
Mit einer Polynomtransformation erster Ordnung werden häufig Bilder geographisch referenziert. Im Folgenden finden Sie die Gleichung zum Transformieren eines Raster-Datasets mit der affinen Polynomtransformation (erster Ordnung). Sie erkennen, in welcher Weise mit sechs Parametern definiert wird, wie die Zeilen und Spalten eines Rasters in Kartenkoordinaten transformiert werden.
Eine polynome Transformation der Ordnung 0 wird für den Datenversatz verwendet. Dies wird häufig verwendet, wenn Daten bereits georeferenziert sind, aber die Daten durch einen kleinen Versatz besser übereinstimmen. Es ist nur ein Link zum Durchführen einer polynomen Transformation 0 erforderlich. Es empfiehlt sich, einige Links zu erstellen und anschließend den Link auszuwählen, der möglichst genau ist.
Verschieben, skalieren und drehen Sie das Raster-Dataset mit einer Transformation erster Ordnung (oder einer affinen Transformation). Gerade Linien auf dem Raster-Dataset werden in der Regel auch im transformierten Raster-Dataset als gerade Linien dargestellt. Daher werden Quadrate und Rechtecke in Parallelogramme beliebigen Maßstabs und beliebiger Winkelausrichtung umgewandelt.
Mit mindestens drei Links kann die mathematische Gleichung, die bei einer Transformation erster Ordnung verwendet wird, jeden Raster-Punkt genau an der Zielposition darstellen. Mehr als drei Links können Fehler oder Residuen hervorrufen, die über alle Links verteilt sind. Sie sollten allerdings mehr Links eingeben, denn wenn nur drei Links verwendet werden und einer davon ungenau ist, hat das noch viel größere Auswirkungen auf die Transformation. Daher erhöht sich die Gesamtgenauigkeit der Transformation, obwohl sich in der mathematischen Transformation durch das Erstellen weiterer Links Fehler ergeben.
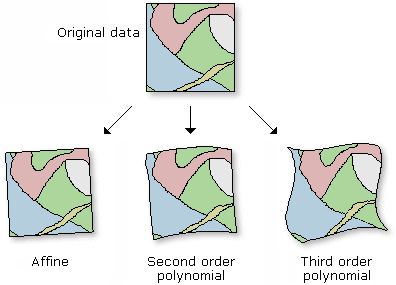
Je höher die Ordnung der Transformation, desto komplexer die Verzerrung, die korrigiert werden kann. Im Allgemeinen benötigen Sie selten Transformationen ab der vierten Ordnung. Für Transformationen höherer Ordnung werden mehr Links benötigt, die wiederum zu deutlich längeren Rechenzeiten führen. Wenn das Raster-Dataset lediglich gestreckt bzw. gestaucht, skaliert und rotiert werden muss, sollten Sie eine Transformation erster Ordnung verwenden. Falls ein Verbiegen des Raster-Datasets nötig ist, sollten Sie eine Transformation zweiter oder dritter Ordnung verwenden.
Die Spline-Transformation ist eine echte Rubbersheeting-Methode, mit der die lokale Genauigkeit optimiert wird, jedoch nicht die globale Genauigkeit. Sie beruht auf einer Spline-Funktion, einem stückweise zusammengesetzten Polynom, in dem Stetigkeit und Glattheit zwischen benachbarten Polynomen beibehalten werden. Bei einem Spline werden die Quellpasspunkte genau in Zielpasspunkte transformiert. Für Pixel abseits der Passpunkte kann keine Genauigkeit gewährleistet werden. Diese Transformation ist hilfreich, wenn die Passpunkte wichtig sind und präzise registriert werden müssen. Durch das Hinzufügen weiterer Passpunkte kann die Gesamtgenauigkeit der Spline-Transformation erhöht werden. Für ein Spline werden mindestens zehn Passpunkte benötigt.
Bei der Anpassungstransformation erfolgt die Optimierung sowohl für die Anpassung mit der Methode der kleinsten Quadrate (LSF) als auch für die lokale Genauigkeit. Sie beruht auf einem Algorithmus, in dem eine Polynomtransformation und TIN-Interpolationen (Triangulated Irregular Network) kombiniert werden. Bei einer Anpassungstransformation wird eine Polynomtransformation mit zwei Gruppen von Passpunkten durchgeführt. Anschließend erfolgt mit einer TIN-Interpolation eine Optimierung der lokalen Anpassung der Passpunkte an die Zielpasspunkte. Für eine Anpassung werden mindestens drei Passpunkte benötigt.
Die projektive Transformation kann Linien so verformen, dass sie gerade bleiben. Dadurch bleiben Linien, die zuvor parallel waren, möglicherweise nicht parallel. Die projektive Transformation ist besonders nützlich für Schrägluftbilder, gescannte Karten und einige Bildprodukte, wie z. B. Landsat und Digital Globe. Mindestens vier Links sind erforderlich, um eine projektive Transformation auszuführen. Wenn nur vier Links verwendet werden, ist der RMS-Fehler 0. Wenn mehr Punkte verwendet werden, ist der RMS-Fehler etwas über 0.
Die Ähnlichkeitstransformation ist eine Transformation erster Ordnung, die versucht, das Shape des ursprünglichen Rasters beizubehalten. Der RMS-Fehler ist tendenziell höher als andere Polynomtransformationen, da die Beibehaltung des Shapes wichtiger ist als die optimale Anpassung.
Interpretieren des RMS-Fehlers
Wenn die generelle Formel abgeleitet und auf den Passpunkt angewendet wurde, wird ein Maß für den Fehler zurückgegeben: der Residuen-Fehler. Der Fehler ist die Differenz zwischen der gesetzten Position der Passpunkte und der Ist-Position des Punktes. Der Gesamtfehler lässt sich über den quadratischen Mittelwert aller Residuen berechnen und ergibt den RMS-Fehler. Dieser Wert beschreibt, wie gleichmäßig die Transformation zwischen den verschiedenen Passpunkten (Links) ist. Bei besonders großen Fehlern können Sie Passpunkte entfernen und hinzufügen, um die Fehler anzupassen.
Der RMS-Fehler kann eine gute Auskunft über die Genauigkeit der Transformation geben. Sie sollten einen niedrigen RMS-Fehler allerdings nicht mit einer genauen Registrierung verwechseln. Die Transformation kann trotzdem erhebliche Fehler enthalten, die z. B. auf einen schlecht eingegebenen Passpunkt zurückzuführen sein können. Je mehr Passpunkte gleicher Qualität Sie einfügen können, desto genauer kann das Polynom die Eingabedaten in Ausgabekoordinaten konvertieren. In der Regel ergibt sich bei Anpassungs- und Spline-Transformationen ein RMS-Fehler von nahe 0 oder gleich 0. Dies bedeutet jedoch nicht, dass das Bild perfekt georeferenziert wird.
Das Vorwärtsresiduum zeigt Ihnen den Fehler in den gleichen Einheiten wie der Datenrahmen-Raumbezug an. Das Inversresiduum zeigt Ihnen den Fehler in den Pixeleinheiten. Das Vorwärts-Inversresiduum ist ein Messwert dafür, wie nah die Genauigkeit ist, gemessen in Pixel. Alle Residuen, die Null am nächsten liegen, gelten als präzisere Residuen.
Resampling des Raster-Datasets
Beim Rektifizieren, Transformieren, Projizieren oder Resampling von Raster-Datasets, beim Konvertieren der Projektion oder beim Ändern der Zellengröße wird eine geometrische Transformation durchgeführt. Als geometrische Transformation wird der Vorgang bezeichnet, die Geometrie eines Raster-Datasets hinsichtlich des Koordinatenbereichs zu ändern. Als Typen geometrischer Transformationen gelten Rubbersheeting (in der Regel bei der geographischen Referenzierung verwendet), Projektion (Transformieren der Daten von einer Projektion in eine andere anhand der Projektionsinformationen), Übertragung (gleichmäßiges Verschieben des Koordinatensystems), Rotation (Drehen sämtlicher Koordinaten um einen bestimmten Winkel) und das Ändern der Zellengröße des Datasets.
Nach dem Anwenden der geometrischen Transformation auf das Eingabe-Raster entsprechen die Zellzentren des Eingabe-Rasters nur selten den Zellzentren des Ausgabe-Rasters. Dennoch müssen den Zentren Werte zugewiesen werden.
Obwohl es scheint, dass jede Zelle eines Raster-Datasets in die Kartenkoordinate transformiert wird, läuft der Prozess in Wirklichkeit umgekehrt ab. Bei der geographischen Referenzierung wird eine Matrix leerer Zellen in Kartenkoordinaten berechnet. Jeder leeren Zelle wird ein Wert zugewiesen, basierend auf einem Prozess, der als Resampling bezeichnet wird.
Die drei bekanntesten Resampling-Methoden sind Nächster-Nachbar-Resampling, bilineare Interpolation und kubische Faltung. Durch diese Methoden wird jeder leeren Zelle ein Wert zugewiesen, indem sie die Zellen im nicht georeferenzierten Raster-Dataset überprüfen.
Nächster-Nachbar-Resampling ist die schnellste Resampling-Methode und für kategorisierte oder thematische Daten geeignet, da sie den Wert der Eingabezellen nicht ändert. Wenn die Position des Zellenmittelpunktes auf dem Ausgabe-Raster-Dataset auch auf dem Eingabe-Raster bekannt ist, bestimmt diese Methode die Position des dichtesten Zellenmittelpunktes auf dem Eingabe-Raster und weist den Wert dieser Zelle der Zelle im Ausgabe-Raster zu.
Nächster-Nachbar-Resampling ändert nicht die Werte der Zellen des Eingabe-Raster-Datasets. Der Wert 2 im Eingabe-Raster bleibt auch im Ausgabe-Raster erhalten und wird nicht in 2,2 oder 3 geändert. Da die Ausgabezellenwerte unverändert bleiben, sollte das Nächster-Nachbar-Resampling für Nominal- oder Ordinaldaten verwendet werden, bei dem jeder Wert eine Klasse, ein Teil oder eine Klassifizierung darstellt – dies können Kategoriedaten wie Landnutzungs-, Boden- oder Waldtyp sein.
Bei der bilinearen Interpolation wird der Wert des Ausgabe-Rasters anhand des Wertes der vier dichtesten Eingabezellzentren bestimmt. Der neue Wert für die Ausgabezelle ist ein gewichteter Durchschnitt dieser vier Werte, der angepasst wurde, um die Entfernung dieser Zellen vom Zentrum der Ausgabezelle im Eingabe-Raster zu berücksichtigen. Diese Interpolationsmethode ergibt eine glatter aussehende Oberfläche als die, die aus der Methode "Nächster-Nachbar-Resampling" entstehen würde.
Da die Werte für die Ausgabezellen nach der relativen Position und dem Wert der Eingabezellen berechnet werden, wird die bilineare Interpolation bevorzugt für Daten verwendet, bei denen die Position eines bekannten Punktes oder eines geographischen Objektes den der Zelle zugewiesenen Wert bestimmt (d. h. kontinuierliche Oberflächen). Die Höhe, die Neigung, der Geräuschpegel eines Flughafens und der Salzgehalt des Grundwassers in der Nähe einer Flussmündung sind Phänomene, die als kontinuierliche Oberflächen dargestellt werden und bei denen mithilfe der bilinearen Interpolation ein sehr genaues Resampling durchgeführt wurde.
Die kubische Faltung ähnelt der bilinearen Interpolation, außer dass hier der gewichtete Durchschnitt aus den 16 dichtesten Eingabezellzentren und deren Werten berechnet wird. Bei der kubischen Faltung werden die Daten i. d. R. stärker als bei der bilinearen Interpolation geschärft, da mehr Zellen in die Berechnung des Ausgabewertes einbezogen werden. Daher wird diese Resampling-Methode häufig beim Resampling von Bildern verwendet, z. B. für Satellitenbilder oder Luftbilder.
Die bilineare Interpolation oder die kubische Faltung sollten nicht für Kategoriedaten verwendet werden, da die Kategorien im Ausgabe-Raster-Dataset nicht erhalten bleiben. Alle drei Methoden können jedoch für kontinuierliche Daten verwendet werden, wobei die Methode "Nächster-Nachbar-Resampling" eine blockförmige Ausgabe, die bilineare Interpolation glattere Ergebnisse und die kubische Faltung Ergebnisse mit scharfer Ausprägung liefert. Bei großen Resampling-Projekten wird empfohlen, einen Prototyp zu erstellen, mehrere Resampling-Verfahren auf diesen anzuwenden und genau auszuwerten, um die für die vorliegenden Daten am besten geeignete Methode zu ermitteln.
Sollten Sie das Raster rektifizieren?
Sie können Raster-Datasets nach der geographischen Referenzierung permanent transformieren, wenn Sie auf der Werkzeugleiste Georeferenzierung den Befehl Rektifizieren auswählen oder das Werkzeug Entzerren verwenden. Sie können die Transformationsinformationen auch in den Zusatzdateien speichern, indem Sie auf der Werkzeugleiste Georeferenzierung den Befehl Georeferenzierung aktualisieren auswählen.
Durch das Rektifizieren oder Entzerren wird ein neues Raster-Dataset erstellt, das über die Kartenkoordinaten und den Raumbezug geographisch referenziert wird. Sie können dieses als Datei in den Formaten BIL, BIP, BMP, BSQ, DAT, GIF, GRID, IMG, JPEG, JPEG 2000, PNG oder TIFF speichern. In ArcGIS müssen Sie Raster-Datasets nicht dauerhaft transformieren, um diese mit anderen räumlichen Daten anzuzeigen. Eine dauerhafte Transformation empfiehlt sich jedoch, wenn Sie eine Analyse durchführen oder das Raster-Dataset in einem anderen Softwarepaket verwenden möchten, in dem externe Informationen zur geographischen Referenzierung, die im World-File erstellt wurden, nicht erkannt werden.
Durch das Aktualisieren der Georeferenzierung werden die Transformationsinformationen in externen Dateien gespeichert. Es wird kein neues Raster-Dataset erstellt. Dies erfolgt nur, wenn Sie das Raster-Dataset dauerhaft transformieren. Bei dateibasierten Raster-Datasets, z. B. im TIFF-Format, wird die Transformation normalerweise in einer externen XML-Datei (mit der Erweiterung .aux.xml) gespeichert. Wenn das Raster-Dataset ein unverarbeitetes Bild (z. B. BMP) und die Transformation affin ist, wird es in ein World-File geschrieben. Bei einem Raster-Dataset in einer Geodatabase wird mit dem Befehl Georeferenzierung aktualisieren die Transformation der geographischen Daten in einer internen Zusatzdatei des Raster-Datasets gespeichert. Durch das Aktualisieren eines Raster-Layers, Image-Services oder Mosaik-Layers wird nur der Layer innerhalb des Kartendokuments aktualisiert. Die Georeferenzierungsinformationen werden nicht wieder in der Quelle gespeichert.
In der nachfolgenden Tabelle wird die Speicherung von Zieltypen dargestellt.
Georeferenzierung von verschiedenen Rastern
| Datentyp | Ergebnis |
|---|---|
Raster-Dataset | Mit dem Befehl Georeferenzierung aktualisieren wird das Raster-Dataset aktualisiert. |
Raster-Layer | Der Raster-Layer wird anhand des Befehls Georeferenzierung aktualisieren aktualisiert. Die Quell-Raster sind hiervon nicht betroffen. |
Image-Service-Layer | Image-Services werden nicht auf dem Server aktualisiert. Nachdem Georeferenzierung aktualisieren ausgeführt wurde, können Sie das Kartendokument (.mxd) speichern oder eine Layer-Datei (.lyr) zum Speichern der Georeferenzierung erstellen. |
Raster-Produkt | Die zugrunde liegenden Raster-Dataset-Dateien werden nicht anhand des Raster-Produkts aktualisiert. Nachdem Georeferenzierung aktualisieren ausgeführt wurde, können Sie das Kartendokument (.mxd) speichern oder eine Layer-Datei (.lyr) zum Speichern der Georeferenzierung erstellen. |
Raster mit einer Funktion | Die zugrunde liegenden Raster-Dateien werden nicht anhand einer Raster-Funktion aktualisiert. Nachdem Georeferenzierung aktualisieren ausgeführt wurde, können Sie das Kartendokument (.mxd) speichern oder eine Layer-Datei (.lyr) zum Speichern der Georeferenzierung erstellen. |