Spatial Autocorrelation (Global Moran's I)

Summary

Measures spatial autocorrelation based on feature locations and attribute values using the Global Moran's I statistic.

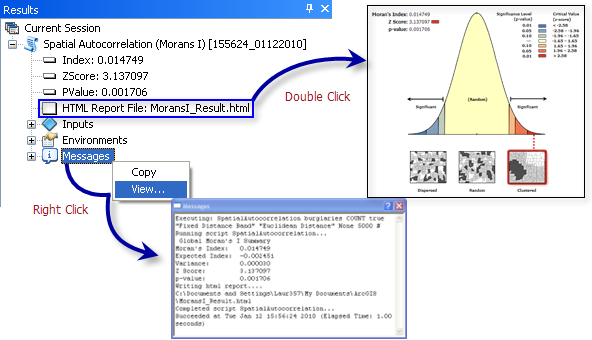
You can access the results of this tool (including the optional report file) from the Results window. If you disable background processing, results will also be written to the Progress dialog box.

Learn more about how Spatial Autocorrelation (Global Moran's I) works

Illustration

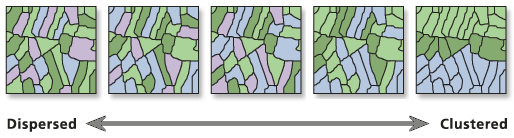
Usage

• The Spatial Autocorrelation tool returns five values: the Moran's I Index, Expected Index, Variance, z-score, and p-value. These values are accessible from the Results window and are also passed as derived output values for potential use in models or scripts. Optionally, this tool will create an HTML file with a graphical summary of results. Double-clicking on the HTML file in the Results window will open the HTML file in the default Internet browser. Right-clicking on the Messages entry in the Results window and selecting View will display the results in a Message dialog box. If you execute this tool in the foreground, output values will also be displayed in the progress dialog box.

  

  Note:

  • If this tool is part of a custom model tool, the HTML link will only appear in the Results window if it is set as a model parameter prior to running the tool.
  • For best display of HTML graphics, ensure your monitor is set to 96 DPI.

• Given a set of features and an associated attribute, this tool evaluates whether the pattern expressed is clustered, dispersed, or random. When the z-score or p-value indicates statistical significance, a positive Moran's I index value indicates tendency toward clustering while a negative Moran's I index value indicates tendency toward dispersion.

• This tool calculates a z-score and p-value to indicate whether or not you can reject the null hypotheses. In this case, the null hypothesis states that features are randomly distributed across the study area.
• The z-score and p-value are measures of statistical significance which tell you whether or not to reject the null hypothesis. For this tool, the null hypothesis states that the values associated with features are randomly distributed.

• The Input Field should contain a variety of values. The math for this statistic requires some variation in the variable being analyzed; it cannot solve if all input values are 1, for example. If you want to use this tool to analyze the spatial pattern of incident data, consider aggregating your incident data. Optimized Hot Spot Analysis may also be used to analyze the spatial pattern of incident data.

  Note:

  Incident data are points representing events (crime, traffic accidents) or objects (trees, stores) where your focus is on presence or absence rather than some measured attribute associated with each point.

• When the Input Feature Class is not projected (that is, when coordinates are given in degrees, minutes, and seconds) or when the output coordinate system is set to a Geographic Coordinate System, distances are computed using chordal measurements. Chordal distance measurements are used because they can be computed quickly and provide very good estimates of true geodesic distances, at least for points within about thirty degrees of each other. Chordal distances are based on an oblate spheroid. Given any two points on the earth's surface, the chordal distance between them is the length of a line, passing through the three-dimensional earth, to connect those two points. Chordal distances are reported in meters.

  Caution:

  Be sure to project your data if your study area extends beyond 30 degrees. Chordal distances are not a good estimate of geodesic distances beyond 30 degrees.

• When chordal distances are used in the analysis, the Distance Band or Threshold Distance parameter, if specified, should be given in meters.

• Prior to ArcGIS 10.2.1, you would see a warning message if the parameters and environment settings you selected would result in calculations being performed using Geographic Coordinates (degrees, minutes, seconds). This warning advised you to project your data into a Projected Coordinate System so that distance calculations would be accurate. Beginning at 10.2.1, however, this tool calculates chordal distances whenever Geographic Coordinate System calculations are required.

  Caution:

  Because of this change, there is a small chance that you will need to modify models that incorporate this tool if your models were created prior to ArcGIS 10.2.1 and if your models include hard-coded Geographic Coordinate System parameter values. If, for example, a distance parameter is set to something like 0.0025 degrees, you will need to convert that fixed value from degrees to meters and resave your model.

Legacy:

In ArcGIS 10, optional graphical output is no longer displayed automatically. Instead, an HTML file summarizing results is created. To view results, double-click the HTML file in the Results window. Custom scripts or model tools created prior to ArcGIS 10 that use this tool may need to be rebuilt. To rebuild these custom tools, open them, remove the Display Results Graphically parameter, and resave.

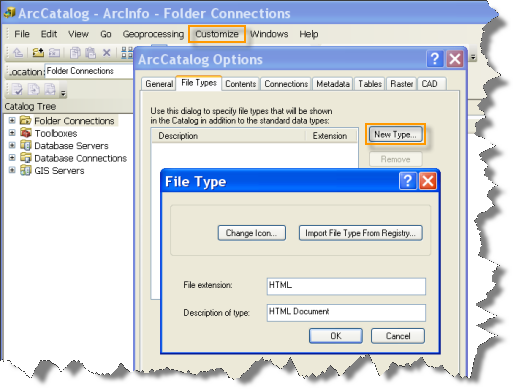
• This tool will optionally create an HTML file summarizing results. HTML files will not automatically appear in the Catalog window. If you want HTML files to be displayed in Catalog, open the ArcCatalog application, select the Customize menu option, click ArcCatalog Options, and select the File Types tab. Click on the New Type button and specify HTML for File Extension.

  

• For line and polygon features, feature centroids are used in distance computations. For multipoints, polylines, or polygons with multiple parts, the centroid is computed using the weighted mean center of all feature parts. The weighting for point features is 1, for line features is length, and for polygon features is area.

• Your choice for the Conceptualization of Spatial Relationships parameter should reflect inherent relationships among the features you are analyzing. The more realistically you can model how features interact with each other in space, the more accurate your results will be. Recommendations are outlined in Selecting a Conceptualization of Spatial Relationships: Best Practices. Here are some additional tips:

  • FIXED_DISTANCE_BAND

    The default Distance Band or Threshold Distance will ensure each feature has at least one neighbor, and this is important. But often, this default will not be the most appropriate distance to use for your analysis. Additional strategies for selecting an appropriate scale (distance band) for your analysis are outlined in Selecting a fixed distance band value.

  • INVERSE_DISTANCE or INVERSE_DISTANCE_SQUARED

    When zero is entered for the Distance Band or Threshold Distance parameter, all features are considered neighbors of all other features; when this parameter is left blank, the default distance will be applied.

    Weights for distances less than 1 become unstable when they are inverted. Consequently, the weighting for features separated by less than 1 unit of distance are given a weight of 1.

    For the inverse distance options (INVERSE_DISTANCE, INVERSE_DISTANCE_SQUARED, or ZONE_OF_INDIFFERENCE), any two points that are coincident will be given a weight of one to avoid zero division. This assures features are not excluded from analysis.

• Additional options for the Conceptualization of Spatial Relationships parameter, including space-time relationships, are available using the Generate Spatial Weights Matrix or Generate Network Spatial Weights tools. To take advantage of these additional options, use one of these tools to construct the spatial weights matrix file prior to analysis; select GET_SPATIAL_WEIGHTS_FROM_FILE for the Conceptualization of Spatial Relationships parameter; and for the Weights Matrix File parameter, specify the path to the spatial weights file you created.

• Map layers can be used to define the Input Feature Class. When using a layer with a selection, only the selected features are included in the analysis.

• If you provide a Weights Matrix File with a .swm extension, this tool is expecting a spatial weights matrix file created using either the Generate Spatial Weights Matrix or Generate Network Spatial Weights tools; otherwise, this tool is expecting an ASCII-formatted spatial weights matrix file. In some cases, behavior is different depending on which type of spatial weights matrix file you use:

  • ASCII-formatted spatial weights matrix files:
    • Weights are used as is. Missing feature-to-feature relationships are treated as zeros.
    • If the weights are row standardized, results will likely be incorrect for analyses on selection sets. If you need to run your analysis on a selection set, convert the ASCII spatial weights file to an SWM file by reading the ASCII data into a table, then using the CONVERT_TABLE option with the Generate Spatial Weights Matrix tool.
  • SWM-formatted spatial weights matrix file:
    • If the weights are row standardized, they will be restandardized for selection sets; otherwise, weights are used as is.

• Running your analysis with an ASCII-formatted spatial weights matrix file is memory intensive. For analyses on more than 5,000 features, consider converting your ASCII-formatted spatial weights matrix file into an SWM-formatted file. First put your ASCII weights into a formatted table (using Excel, for example). Next, run the Generate Spatial Weights Matrix tool using CONVERT_TABLE for the Conceptualization of Spatial Relationships parameter. The output will be an SWM-formatted spatial weights matrix file.

Note:

It is possible to run out of memory when you run this tool. This generally occurs when you select Conceptualization of Spatial Relationships and Distance Band or Threshold Distance resulting in features having many, many neighbors. You generally do not want to define spatial relationships so that features have thousands of neighbors. You want all features to have at least one neighbor and almost all features to have at least eight neighbors.

• For polygon features, you will almost always want to choose ROW for the Standardization parameter. Row Standardization mitigates bias when the number of neighbors each feature has is a function of the aggregation scheme or sampling process, rather than reflecting the actual spatial distribution of the variable you are analyzing.

• The Modeling Spatial Relationships help topic provides additional information about this tool's parameters.

Caution:

When using shapefiles, keep in mind that they cannot store null values. Tools or other procedures that create shapefiles from nonshapefile inputs may store or interpret null values as zero. In some cases, nulls are stored as very large negative values in shapefiles. This can lead to unexpected results. See Geoprocessing considerations for shapefile output for more information.

Syntax

SpatialAutocorrelation_stats (Input_Feature_Class, Input_Field, {Generate_Report}, Conceptualization_of_Spatial_Relationships, Distance_Method, Standardization, {Distance_Band_or_Threshold_Distance}, {Weights_Matrix_File})

Parameter	Explanation	Data Type
Input_Feature_Class	The feature class for which spatial autocorrelation will be calculated.	Feature Layer
Input_Field	The numeric field used in assessing spatial autocorrelation.	Field
Generate_Report (Optional)	NO_REPORT —No graphical summary will be created. This is the default. GENERATE_REPORT —A graphical summary will be created as an HTML file.	Boolean
Conceptualization_of_Spatial_Relationships	Specifies how spatial relationships among features are defined. INVERSE_DISTANCE —Nearby neighboring features have a larger influence on the computations for a target feature than features that are far away. INVERSE_DISTANCE_SQUARED —Same as INVERSE_DISTANCE except that the slope is sharper, so influence drops off more quickly, and only a target feature's closest neighbors will exert substantial influence on computations for that feature. FIXED_DISTANCE_BAND —Each feature is analyzed within the context of neighboring features. Neighboring features inside the specified critical distance (Distance_Band_or_Threshold) receive a weight of one and exert influence on computations for the target feature. Neighboring features outside the critical distance receive a weight of zero and have no influence on a target feature's computations. ZONE_OF_INDIFFERENCE —Features within the specified critical distance (Distance_Band_or_Threshold) of a target feature receive a weight of one and influence computations for that feature. Once the critical distance is exceeded, weights (and the influence a neighboring feature has on target feature computations) diminish with distance. CONTIGUITY_EDGES_ONLY —Only neighboring polygon features that share a boundary or overlap will influence computations for the target polygon feature. CONTIGUITY_EDGES_CORNERS —Polygon features that share a boundary, share a node, or overlap will influence computations for the target polygon feature. GET_SPATIAL_WEIGHTS_FROM_FILE —Spatial relationships are defined by a specified spatial weights file. The path to the spatial weights file is specified by the Weights_Matrix_File parameter.	String
Distance_Method	Specifies how distances are calculated from each feature to neighboring features. EUCLIDEAN_DISTANCE —The straight-line distance between two points (as the crow flies) MANHATTAN_DISTANCE —The distance between two points measured along axes at right angles (city block); calculated by summing the (absolute) difference between the x- and y-coordinates	String
Standardization	Row standardization is recommended whenever the distribution of your features is potentially biased due to sampling design or an imposed aggregation scheme. NONE —No standardization of spatial weights is applied. ROW —Spatial weights are standardized; each weight is divided by its row sum (the sum of the weights of all neighboring features).	String
Distance_Band_or_Threshold_Distance (Optional)	Specifies a cutoff distance for the inverse distance and fixed distance options. Features outside the specified cutoff for a target feature are ignored in analyses for that feature. However, for ZONE_OF_INDIFFERENCE, the influence of features outside the given distance is reduced with distance, while those inside the distance threshold are equally considered. The distance value entered should match that of the output coordinate system. For the inverse distance conceptualizations of spatial relationships, a value of 0 indicates that no threshold distance is applied; when this parameter is left blank, a default threshold value is computed and applied. This default value is the Euclidean distance that ensures every feature has at least one neighbor. This parameter has no effect when polygon contiguity (CONTIGUITY_EDGES_ONLY or CONTIGUITY_EDGES_CORNERS) or GET_SPATIAL_WEIGHTS_FROM_FILE spatial conceptualizations are selected.	Double
Weights_Matrix_File (Optional)	The path to a file containing weights that define spatial, and potentially temporal, relationships among features.	File

Derived Output

Name	Explanation	Data Type
Index
ZScore
PValue
Report_File

Code sample

SpatialAutocorrelation example 1 (Python window)

The following Python window script demonstrates how to use the SpatialAutocorrelation tool.

import arcpy
arcpy.env.workspace = r"c:\data"
arcpy.SpatialAutocorrelation_stats("olsResults.shp", "Residual","NO_REPORT", 
                                   "GET_SPATIAL_WEIGHTS_FROM_FILE","EUCLIDEAN DISTANCE", 
                                   "NONE", "#","euclidean6Neighs.swm")

SpatialAutocorrelation example 2 (stand-alone Python script)

The following stand-alone Python script demonstrates how to use the SpatialAutocorrelation tool.

# Analyze the growth of regional per capita incomes in US
# Counties from 1969 -- 2002 using Ordinary Least Squares Regression

# Import system modules
import arcpy

# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True

# Local variables...
workspace = r"C:\Data"

try:
    # Set the current workspace (to avoid having to specify the full path to the feature classes each time)
    arcpy.env.workspace = workspace

    # Growth as a function of {log of starting income, dummy for South
    # counties, interaction term for South counties, population density}
    # Process: Ordinary Least Squares... 
    ols = arcpy.OrdinaryLeastSquares_stats("USCounties.shp", "MYID", 
                        "olsResults.shp", "GROWTH",
                        "LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
                        "olsCoefTab.dbf",
                        "olsDiagTab.dbf")

    # Create Spatial Weights Matrix (Can be based off input or output FC)
    # Process: Generate Spatial Weights Matrix... 
    swm = arcpy.GenerateSpatialWeightsMatrix_stats("USCounties.shp", "MYID",
                        "euclidean6Neighs.swm",
                        "K_NEAREST_NEIGHBORS",
                        "#", "#", "#", 6) 
                        

    # Calculate Moran's I Index of Spatial Autocorrelation for 
    # OLS Residuals using a SWM File.  
    # Process: Spatial Autocorrelation (Morans I)...      
    moransI = arcpy.SpatialAutocorrelation_stats("olsResults.shp", "Residual",
                        "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE", 
                        "EUCLIDEAN_DISTANCE", "NONE", "#", 
                        "euclidean6Neighs.swm")

except:
    # If an error occurred when running the tool, print out the error message.
    print(arcpy.GetMessages())

Environments

• Current Workspace
• Scratch Workspace
• Output Coordinate System

  Note:

  Feature geometry is projected to the Output Coordinate System prior to analysis. All mathematical computations are based on the Output Coordinate System spatial reference. When the Output Coordinate System is based on degrees, minutes, and seconds, geodesic distances are estimated using chordal distances.

• Geographic Transformations

Licensing information

• ArcGIS Desktop Basic: Yes
• ArcGIS Desktop Standard: Yes
• ArcGIS Desktop Advanced: Yes