Cómo funciona Vecino natural

Disponible con una licencia de Spatial Analyst.

El algoritmo utilizado por la herramienta de interpolación de Vecino natural halla el subconjunto de muestras de entrada más cercano a un punto de consulta y aplica ponderaciones sobre éstas basándose en áreas proporcionales para interpolar un valor (Sibson, 1981). También se conoce como interpolación de Sibson o de "robo de área". Sus propiedades básicas son que es local, utiliza sólo un subconjunto de muestras que circundan a un punto de consulta y asegura que las alturas interpoladas estarán dentro del rango de las muestras utilizadas. No infiere tendencias ni produce picos, depresiones, crestas o valles que no estén ya representados por las muestras de entrada. La superficie pasa por las muestras de entrada y es suave en todas partes, excepto en las ubicaciones de las muestras de entrada.

Sugerencia:

Si tiene la extensión 3D Analyst, puede utilizar la herramienta De TIN a ráster para incorporar líneas de corte a la interpolación. Éstas pueden aumentar los resultados de la interpolación y crear discontinuidades lineales donde sea adecuado, como a lo largo de los bordes de las carreteras y los cuerpos hídricos. Se adapta localmente a la estructura de los datos de entrada, sin requerir entrada del usuario relativa al radio de búsqueda, el conteo de las muestras o a la forma. Funciona bien tanto con los datos distribuidos regularmente como irregularmente (Watson 1992).

Los vecinos naturales de un punto son aquellos que están asociados con los polígonos de Voronoi (Thiessen) adyacentes. Al principio, se construye un diagrama de Voronoi de todos los puntos dados, representados por los polígonos de color verde oliva. Después se crea un nuevo polígono de Voronoi, en color beige, alrededor del punto de interpolación (estrella roja). La proporción de superposición entre este polígono nuevo y los polígonos iniciales se utiliza como ponderaciones.

Ejemplo de polígono de Voronoi creado alrededor del punto de interpolación

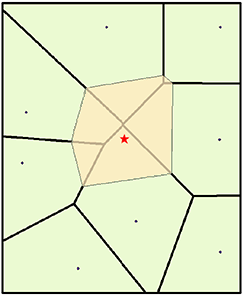
Por comparación, una herramienta de interpolación basada en la distancia como IDW (Distancia inversa ponderada) asignaría ponderaciones similares al punto que se encuentra más al norte y al que se encuentra más al noreste, basándose en su distancia similar desde el punto de interpolación. La interpolación de vecino natural, no obstante, asigna ponderaciones de 19,12% y 0,38%, respectivamente, que están basadas en el porcentaje de superposición.

Referencias

Sibson, R. "A Brief Description of Natural Neighbor Interpolation", capítulo 2 de Interpolating Multivariate Data. John Wiley & Sons: Nueva York, 1981, 21–36.

Watson, D.Contouring: A Guide to the Analysis and Display of Spatial Data. Pergamon Press: Londres, 1992.

¿Algún comentario sobre este tema?