Disponible con una licencia de Geostatistical Analyst.
Una de las decisiones más importantes que tendrá que tomar es cuáles son sus objetivos al desarrollar un modelo de interpolación. En otras palabras: qué información necesita que el modelo proporcione para poder tomar una decisión. Por ejemplo, en el ámbito de la salud pública, se usan modelos de interpolación para predecir los niveles de contaminantes que se pueden asociar estadísticamente con tasas de enfermedad. A partir de esa información, se pueden diseñar otros estudios de muestreo, directivas de salud pública, etc.
Geostatistical Analyst ofrece muchos métodos de interpolación diferentes. Cada uno de ellos tiene cualidades únicas y proporciona informaciones diferentes (en algunos casos, los métodos proporcionan una información similar; en otros, la información puede ser muy distinta). Los siguientes diagramas muestran estos métodos clasificados según distintos criterios. Elija un criterio que sea importante para su situación concreta y una rama del árbol correspondiente que represente la opción que le interesa. Esto le llevará a uno o varios métodos de interpolación que pueden ser adecuados para su situación. Muy probablemente habrá varios criterios importantes que desee cumplir y usará varios de los árboles de clasificación. Compare los métodos de interpolación sugeridos por cada rama del árbol que siga y elija varios métodos para compararlos antes de decidirse por un modelo final.
El primer árbol sugiere métodos en función de la capacidad que estos tienen de generar predicciones o predicciones y errores asociados.
Algunos métodos requieren un modelo de autocorrelación espacial para generar valores predichos, pero otros no. Un modelo de autocorrelación espacial exige definir valores de parámetros adicionales y ajustar un modelo a los datos de forma interactiva.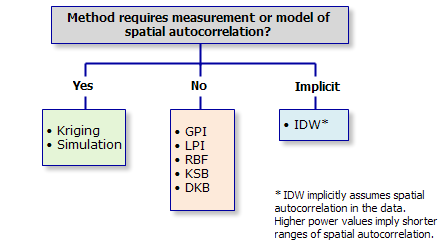
Distintos métodos generan diferentes tipos de salidas y esa es la razón por la que debe decidir el tipo de información que necesita generar antes de crear el modelo de interpolación. 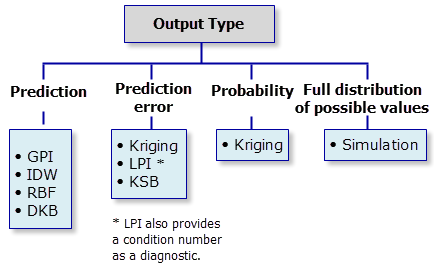
Los métodos de interpolación difieren en sus niveles de complejidad, que se puede medir por el número de suposiciones que se deben cumplir para que el modelo sea válido. 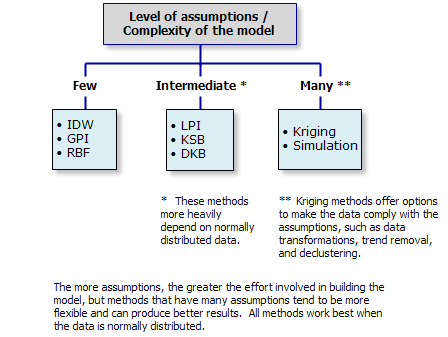
Algunos interpoladores son exactos (en cada ubicación de datos de entrada, la superficie tendrá exactamente el mismo valor que el valor de los datos de entrada), mientras que otros no lo son. Una replicación exacta de los datos de entrada puede ser importante en algunas situaciones. 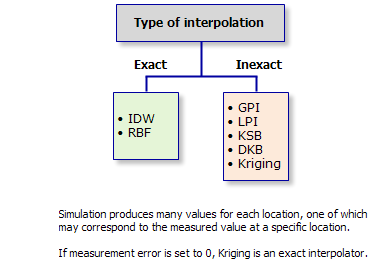
Algunos métodos producen superficies que son más suaves que las generadas por otros. Las funciones de base radial son suaves por definición, por ejemplo. Una vecindad de búsqueda suave producirá superficies más suaves que una vecindad de búsqueda estándar. 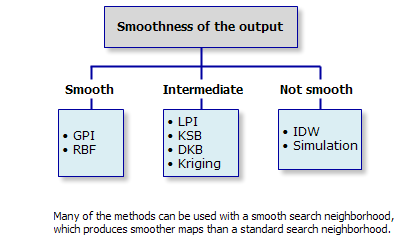
Para algunas decisiones, es importante considerar no solo el valor predicho para una ubicación, sino también la incertidumbre (variabilidad) asociada con esa predicción. Algunos métodos proporcionan medidas de la incertidumbre, mientras que otros no lo hacen. 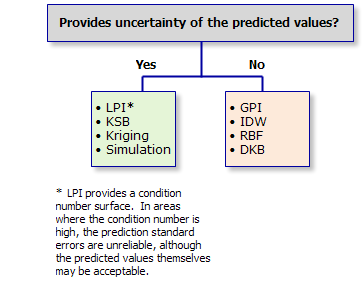
Por último, la velocidad de procesamiento puede ser un factor en el análisis. En general, la mayoría de los métodos de interpolación son relativamente rápidos, salvo cuando las barreras se usan para controlar el proceso de interpolación. 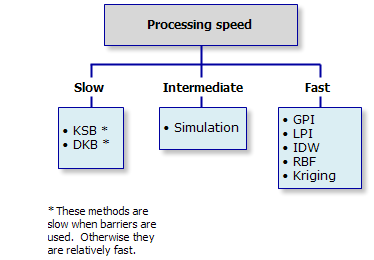
Los árboles de clasificación usan las siguientes abreviaturas para los métodos de interpolación:
| Abreviatura | Nombre del método |
|---|---|
GPI | |
LPI | |
IDW | |
RBF | |
KSB | |
DKB | |
Kriging | Ordinario, simple, universal, indicador, de probabilidad, disyuntivo y kriging bayesiano empírico |
Simulación | Simulación gaussiana de estadísticas geográficas, basada en un modelo de kriging simple. |