Uso de las funciones de base radial

Disponible con una licencia de Geostatistical Analyst.

Las funciones de base radial (RBF) son una serie de técnicas de interpolación exacta, es decir: la superficie debe pasar por cada valor de muestra medido. Hay cinco funciones de base diferentes:

• Spline de lámina delgada
• Spline con tensión
• Spline regularizado completamente
• Función multicuádrica
• Función multicuádrica inversa

Cada función de base tiene una forma diferente y genera una superficie de interpolación distinta. Los métodos RBF son un caso especial de splines.

Las RBF son conceptualmente similares a ajustar una membrana de goma a través de los valores de muestra medidos minimizando a la vez la curvatura total de la superficie. La función de base seleccionada determina cómo se ajustará la membrana de goma entre los valores. El siguiente diagrama ilustra conceptualmente cómo se ajusta una superficie RBF a través de una serie de valores de muestra de elevación. Como puede ver en la sección cruzada, la superficie pasa por los valores de datos.

Sección cruzada que ilustra cómo se ajusta la superficie RBF a los valores de muestra

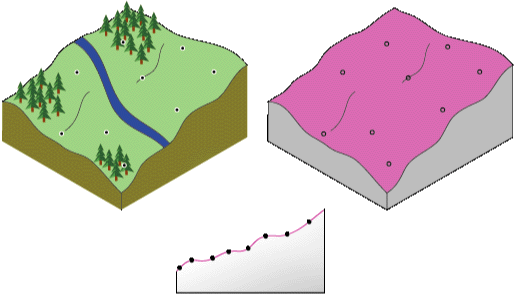
Los métodos RBF, como interpoladores exactos, son distintos de los interpoladores polinómicos globales y locales, que son interpoladores inexactos que no requieren que la superficie pase por los puntos medidos. Si se compara una RBF con el método IDW (que también es un interpolador exacto), IDW nunca predice valores por encima del valor máximo medido o por debajo del valor mínimo medido, como se puede ver en la sección cruzada del corte de datos de muestra que aparece a continuación.

Ejemplo de perfil de la Distancia inversa ponderada

Sin embargo, las RBF pueden predecir valores por encima del valor máximo medido y por debajo del mínimo, como se ve en la sección cruzada siguiente.

Ejemplo de sección cruzada de RBF

Los parámetros óptimos se determinan usando la validación cruzada de un modo similar al descrito para el método IDW y la interpolación polinómica local.

Cuándo se deben usar las funciones de base radial

Las RBF se usan para generar superficies suaves a partir de un gran número de puntos de datos. Las funciones producen buenos resultados para superficies con una variación suave como la elevación.

Sin embargo, las técnicas no son adecuadas cuando se producen cambios grandes de los valores de la superficie en distancias cortas o cuando se sospecha que los datos de la muestra son proclives a los errores de medición o a las incertidumbres.

Conceptos relacionados con las funciones de base radial

En Geostatistical Analyst, las RBF se forman sobre cada ubicación de datos. Una RBF es una función que cambia con la distancia a una ubicación.

Funciones RBF para distintas ubicaciones

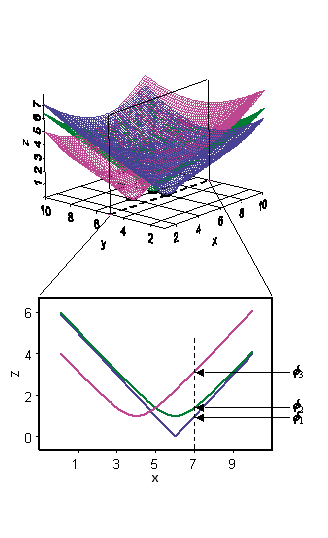
Por ejemplo, suponga que la función de base radial es simplemente la distancia a cada ubicación, con lo que forma un cono invertido sobre cada ubicación. Si toma una sección cruzada del plano x,z para y = 5, verá un corte de cada función de base radial. Suponga ahora que desea predecir un valor para y = 5 y x = 7. El valor de cada función de base radial en la ubicación de predicción se puede tomar de la figura anterior, dada por los valores Φ₁, Φ₂ y Φ₃, que dependen simplemente de la distancia a cada ubicación de datos. La predicción se obtiene tomando el promedio ponderado w₁Φ₁ + w₂Φ₂ + w₃Φ₃ + …

Veamos ahora cómo se determinan los pesos. Hasta el momento, no ha usado para nada los valores de datos. Los pesos w₁, w₂, w₃, etc. se encuentran exigiendo que, cuando la predicción se mueva a una ubicación con un valor medido, el valor de datos se prediga con exactitud. Esto forma N ecuaciones con N incógnitas que tienen soluciones únicas. De este modo, la superficie pasa por los valores de datos y las predicciones son exactas.

La función de base radial de este ejemplo es un caso especial de RBF multicuadrática. Geostatistical Analyst también permite usar otras RBF como las splines totalmente regularizadas, las splines de lámina delgada, las splines con tensión y la multicuadrática inversa. En algunos casos, no hay gran diferencia entre ellas, pero puede tener razones para elegir una o puede probar varias y usar la validación cruzada para seleccionar una. Cada una de las funciones de base radial tiene un parámetro que controla la suavidad de la superficie.

Para todos los métodos, excepto el multicuadrático inverso, cuanto mayor sea el valor del parámetro, más suave será el mapa. Y en el caso del multicuadrático inverso ocurre lo contrario.