Resumen
Realiza una Regresión ponderada geográficamente (GWR), una forma local de regresión lineal que se utiliza para modelar las relaciones que varían espacialmente.
Más información sobre cómo funciona Regresión ponderada geográficamente
Ilustración
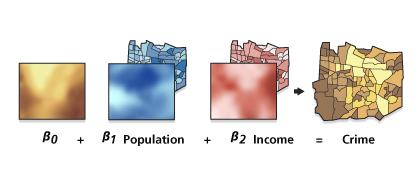
Uso
GWR construye una ecuación distinta para cada entidad en el dataset al incorporar las variables dependientes y explicativas de las entidades que caen dentro del ancho de banda de cada entidad de destino. La forma y la extensión del ancho de banda depende de la entrada del usuario para los parámetros Tipo Kernel (núcleo), Método Ancho de banda, Distancia y Cantidad de vecinos con una restricción: si el número de entidades vecinas es superior a 1000, solo se incorporarán a cada ecuación local las 1000 más próximas.
Para obtener mejores resultados, GWR se debe aplicar a los datasets con varios cientos de entidades. No es un método adecuado para datasets pequeños. La herramienta no funciona con datos de multipunto.
La herramienta GWR también produce una Clase de entidad de salida y una tabla con los valores de diagnóstico del informe del resumen de ejecución de la herramienta. El nombre de esta tabla se genera automáticamente utilizando el nombre de la clase de entidad de salida con el sufijo _supp. La Clase de entidad de salida se agrega automáticamente a la tabla de contenido con un esquema de representación cálida/fría aplicado a los residuales del modelo. En Interpretar los resultados de GWR se proporciona una explicación completa de cada salida.
El archivo _supp se crea siempre en la misma ubicación que la Clase de entidad de salida, a menos que esta clase se cree dentro de un dataset de entidades. Si la clase de entidad de salida está dentro de un dataset de entidades, la tabla _supp se crea en la geodatabase que contiene el dataset de entidades.
Se recomienda utilizar siempre datos proyectados; esto es especialmente importante cuando la distancia es un componente del análisis, como lo es para GWR cuando selecciona Fijo para el Tipo Kernel (núcleo). Se recomienda que los datos estén proyectados mediante un Sistema de coordenadas proyectadas (en lugar de un Sistema de coordenadas geográficas).
Algunos de los cómputos que realiza la herramienta GWR aprovechan varias CPU para incrementar el rendimiento y utilizarán automáticamente hasta ocho subprocesos/CPU para el procesamiento.
El análisis de regresión debe comenzar siempre con la regresión Mínimos cuadrados ordinarios (OLS). En primer lugar, busque un modelo OLS especificado adecuadamente, después utilice las mismas variables explicativas para ejecutar GWR (excluya todas las variables explicativas "dummy" que representen distintos regímenes espaciales).
Las variables dependientes y explicativas deben ser campos numéricos que contengan una variedad de valores. Los métodos de regresión lineal, como GWR, no son adecuados para prever resultados binarios (por ej., todos los valores para la variable dependiente son 1 o 0).
En los modelos de regresión global, como la Regresión de mínimos cuadrados ordinarios (OLS), los resultados son poco confiables cuando dos o más variables exhiben multicolinealidad (cuando dos o más variables son redundantes o cuentan la misma "historia"). GWR construye una ecuación de regresión local para cada entidad en el dataset. Cuando los valores para una variable explicativa particular se agrupan espacialmente, es muy probable que tenga problemas con la multicolinealidad local. El campo del número de condición (COND) de la clase de entidad de salida indica el momento en el que los resultados son inestables debido a la multicolinealidad local. Como regla general, no confíe en los resultados para las entidades que tengan un número de condición mayor que 30, igual a Nulo, o, para los shapefiles, igual a -1,7976931348623158e+308.
Tenga precaución al incluir datos nominales o categóricos en un modelo GWR. Donde las categorías se agrupan espacialmente, existe un gran riesgo de encontrar problemas de multicolinealidad local. El número de condición incluido en la salida de GWR indica cuando la colinealidad local es un problema (un número de condición menor que cero, mayor que 30 o establecido en Nulo). Cuando existe una multicolinealidad local, los resultados son inestables.
No utilice variables explicativas "dummy" para representar regímenes espaciales diferentes en un modelo GWR (por ej. a los distritos censales que están fuera del núcleo urbano se les asigna un valor de 1, mientras que al resto se les asigna un valor de 0). Ya que GWR permite que los coeficientes de la variable explicativa varíen, estas variables explicativas del régimen espacial no son necesarias, y si se incluyen, crearán problemas con la multicolinealidad local.
Para comprender mejor la variación regional entre los coeficientes de las variables explicativas, examine las superficies de ráster de coeficiente opcionales creadas por GWR. Estas superficies de ráster se crean en el Espacio de trabajo coeficiente ráster, si especifica una superficie. Para los datos de polígono, puede utilizar un color graduado o una representación fría a cálida en cada campo de coeficiente en la Clase de entidad de salida para examinar los cambios en el área de estudio.
Puede utilizar GWR para hacer una predicción al suministrar una clase de entidad de Predicción ubicaciones (a menudo, esta clase de entidad es la misma que la Clase de entidad de entrada), las Variables explicativas de predicción y una Salida predicción clase de entidad. Debe haber una correspondencia de uno a uno entre los campos utilizados para calibrar el modelo de regresión (los valores introducidos para el campo Variables explicativas) y los campos utilizados para la predicción (los valores introducidos para el campo Variables explicativas de predicción). El orden de estas variables debe ser el mismo. Por ejemplo, supongamos que está modelando accidentes de tráfico como una función de límites de velocidad, condiciones de carretera, cantidad de vías y cantidad de autos. Puede prever el impacto que podría tener el cambio de los límites de velocidad o la mejora de las carreteras en los accidentes de tráfico mediante la creación de nuevas variables con los límites de velocidad y las condiciones de carretera corregidos. Las variables existentes se utilizarían para calibrar el modelo de regresión y para el parámetro Variables explicativas. Las variables corregidas se utilizarían para las predicciones y serían introducidas como Variables explicativas de predicción.
Si se proporciona una clase de entidad de Predicción ubicaciones, pero no se especifican las Variables explicativas de predicción, se crea la Salida predicción clase de entidad solo con los coeficientes calculados para cada ubicación (sin predicciones).
Un modelo de regresión está mal especificado si falta una variable explicativa clave. La autocorrelación espacial de los residuales de regresión o la variación espacial no esperada entre los coeficientes de una o más variables explicativas que sean estadísticamente significativas sugieren que el modelo está mal especificado. Debe hacer todo el esfuerzo posible (por ejemplo, a través del análisis de residual OLS y el análisis de variación del coeficiente GWR) para descubrir cuáles son las variables clave que faltan para poder incluirlas en el modelo.
Pregúntese siempre si tiene sentido que una variable explicativa sea no estacionaria. Por ejemplo, supongamos que está modelando la densidad de una especie de planta en particular como función de muchas variables incluida la de la ORIENTACIÓN. Si descubre que el coeficiente de la variable ORIENTACIÓN en el área de estudio cambia, es probable que sea la evidencia de que falta una variable explicativa clave (tal vez, la prevalencia de una vegetación rival, por ejemplo). Debe hacer todo el esfuerzo posible para incluir todas las variables explicativas clave en el modelo de regresión.
Cuando el resultado de un cálculo es infinito o indefinido, el resultado para los no shapefiles será Nulo; para los shapefiles el resultado será -DBL_MAX = -1,7976931348623158e+308.
Cuando selecciona AICc (Criterio de información de Akaike corregido) o CV (Cross Validation) para el parámetro Método ancho de banda, GWR buscará la distancia óptima (para un kernel fijo) o la cantidad óptima de vecinos (para un kernel adaptable). Sin embargo, los problemas con la multicolinealidad local evitarán que los métodos de ancho de banda AICc y CV resuelvan una distancia/cantidad de vecinos óptimas. Si aparece un error que indica problemas graves de diseño del modelo, trate de especificar una distancia o un número de vecinos en particular, después examine los números de condiciones en la clase de entidad de salida para ver qué entidades están asociadas con los problemas de colinealidad local.
Los errores graves de diseño del modelo o los errores que indican que las ecuaciones locales no incluyen suficientes vecinos, por lo general señalan que existe un problema con la multicolinealidad global o local. Para determinar dónde está el problema, ejecute el modelo con OLS y examine el valor VIF para cada variable explicativa. Si algunos de los valores VIF son grandes (por ejemplo, mayores que 7,5), la multicolinealidad global impide que se resuelva la RPG. Sin embargo, es más probable que la multicolinealidad local sea el problema. Intente crear un mapa temático para cada variable explicativa. Si el mapa muestra un clustering espacial de valores idénticos, considere eliminar esas variables del modelo o combinarlas con otras variables explicativas para amentar la variación del valor. Por ejemplo, si está modelando valores de viviendas y tiene variables tanto para los dormitorios como para los cuartos de baño, es posible que desee combinarlas para aumentar la variación del valor o para representarlas como pies cuadrados de cuarto de baño/dormitorio. Evite utilizar variables dummy del régimen espacial, variables categóricas/nominales de clustering espacial o variables con pocos valores posibles al construir modelos GWR.
GWR es un modelo lineal que está sujeto a los mismos requisitos que OLS. Revise la sección Cómo dejan de funcionar los modelos de regresión en el documento Conceptos básicos del análisis de regresión para verificar que su modelo GWR esté especificado correctamente.
Sintaxis
GeographicallyWeightedRegression_stats (in_features, dependent_field, explanatory_field, out_featureclass, kernel_type, bandwidth_method, {distance}, {number_of_neighbors}, {weight_field}, {coefficient_raster_workspace}, {cell_size}, {in_prediction_locations}, {prediction_explanatory_field}, {out_prediction_featureclass})| Parámetro | Explicación | Tipo de datos |
in_features | La clase en entidad que contiene las variables dependientes e independientes. | Feature Layer |
dependent_field | El campo numérico que contiene los valores de aquello que intenta modelar. | Field |
explanatory_field [explanatory_field,...] | Una lista de campos que representan variables explicativas independientes en el modelo de regresión. | Field |
out_featureclass | La clase de entidad de salida que recibirá estimaciones y residuales de variables dependientes. | Feature Class |
kernel_type | Especifica si el kernel se construye como una distancia fija o si puede variar en extensión como una función de la densidad de entidad.
| String |
bandwidth_method | Especifica cómo se debe determinar la extensión del kernel. Cuando se selecciona AICc o CV, la herramienta buscará la distancia o el número de vecinos óptimos. Normalmente seleccionará AICc o CV si no está seguro de lo que debe utilizar para los parámetros de Distancia o Cantidad de vecinos. Sin embargo, una vez que la herramienta determine la distancia o el número de vecinos óptimos, deberá utilizar la opción BANDWIDTH_PARAMETER.
| String |
distance (Opcional) | La distancia siempre que el kernel_type es FIXED y el bandwidth_method es BANDWIDTH_PARAMETER. | Double |
number_of_neighbors (Opcional) | Cantidad exacta de vecinos para incluir en el ancho de banda local del kernel gaussiano cuando kernel_type es ADAPTIVE y el bandwidth_method es BANDWIDTH_PARAMETER. | Long |
weight_field (Opcional) | El campo numérico que contiene una ponderación espacial para las entidades individuales. Este campo de peso permite que algunas entidades sean más importantes que otras en el proceso de calibración del modelo. Es útil principalmente cuando el número de muestras tomadas en diferentes ubicaciones varía, los valores de las variables dependientes e independientes se promedian y los lugares con más muestras son más confiables (deben tener una mayor ponderación). Si tiene un promedio de 25 muestras diferentes para una ubicación, pero un promedio de solo 2 muestras para otra, puede utilizar el número de muestras como campo de peso para que las ubicaciones con más muestras tengan mayor influencia en la calibración del modelo que las ubicaciones con pocas muestras. | Field |
coefficient_raster_workspace (Opcional) | Una ruta de acceso completa al espacio de trabajo donde se crearán todos los rásteres de coeficiente. Cuando se proporciona este espacio de trabajo, se crean rásteres para la intercepción y para cada variable explicativa. | Workspace |
cell_size (Opcional) | El tamaño de celda (un número) o la referencia al tamaño de celda (una ruta de acceso al dataset ráster) para utilizar cuando se crean los rásteres de coeficiente. El tamaño de celda predeterminado es el más corto del ancho o la altura de la extensión especificada en el sistema de coordenadas de salida del entorno de geoprocesamiento, dividido por 250. | Analysis cell size |
in_prediction_locations (Opcional) | Una clase de entidad que contiene entidades que representan ubicaciones donde se deben realizar los cálculos. Cada entidad en este dataset debe incluir valores para todas las variables explicativas especificadas; la variable dependiente para estas entidades se calculará con el modelo calibrado para los datos de la clase de entidad de entrada. | Feature Layer |
prediction_explanatory_field [prediction_explanatory_field,...] (Opcional) | Una lista de campos que representan las variables explicativas en la clase de entidad de Predicción ubicaciones. Los nombres de estos campos se deben proporcionar en el mismo orden (una correspondencia de uno a uno) que los nombres enumerados para el parámetro Variables explicativas de la clase de entidad de entrada. Si no se proporcionan variables explicativas de predicción, la clase de entidad de predicción de salida solo incluirá valores de coeficiente calculados para cada ubicación de predicción. | Field |
out_prediction_featureclass (Opcional) | La clase de entidad de salida que recibirá los cálculos de la variable dependiente para cada entidad en la clase de entidad de Predicción ubicaciones. | Feature Class |
Muestra de código
Ejemplo de GeographicallyWeightedRegression (ventana de Python)
La siguiente secuencia de comandos de la ventana de Python muestra cómo utilizar la herramienta GeographicallyWeightedRegression.
import arcpy
arcpy.env.workspace = "c:/data"
arcpy.GeographicallyWeightedRegression_stats("CallData.shp", "Calls","BUS_COUNT;RENTROCC00;NoHSDip",
"CallsGWR.shp", "ADAPTIVE", "BANDWIDTH PARAMETER",
"#", "25", "#","CoefRasters", "135", "PredictionPoints",
"#", "GWRCallPredictions.shp")
Ejemplo de GeographicallyWeightedRegression (secuencia de comandos de Python independiente)
La siguiente secuencia de comandos de Python independiente muestra cómo utilizar la herramienta GeographicallyWeightedRegression.
# Model 911 emergency calls using GWR
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\Data"
try:
# Set the current workspace (to avoid having to specify the full path to the feature classes each time)
arcpy.env.workspace = workspace
# 911 Calls as a function of {number of businesses, number of rental units,
# number of adults who didn't finish high school}
# Process: Geographically Weighted Regression...
gwr = arcpy.GeographicallyWeightedRegression_stats("CallData.shp", "Calls",
"BUS_COUNT;RENTROCC00;NoHSDip",
"CallsGWR.shp", "ADAPTIVE", "BANDWIDTH PARAMETER","#", "25", "#",
"CoefRasters", "135", "PredictionPoints", "#", "GWRCallPredictions.shp")
# Create Spatial Weights Matrix to use with Global Moran's I tool
# Process: Generate Spatial Weights Matrix...
swm = arcpy.GenerateSpatialWeightsMatrix_stats("CallsGWR.shp", "UniqID",
"CallData25Neighs.swm",
"K_NEAREST_NEIGHBORS",
"#", "#", "#", 25)
# Calculate Moran's Index of Spatial Autocorrelation for
# OLS Residuals using a SWM File.
# Process: Spatial Autocorrelation (Morans I)...
moransI = arcpy.SpatialAutocorrelation_stats("CallsGWR.shp", "StdResid",
"NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "NONE", "#",
"CallData25Neighs.swm")
except:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())
Entornos
Información sobre licencias
- ArcGIS Desktop Basic: Requiere Spatial Analyst o Geostatistical Analyst
- ArcGIS Desktop Standard: Requiere Spatial Analyst o Geostatistical Analyst
- ArcGIS Desktop Advanced: Sí