Disponible avec une licence Geostatistical Analyst.
Génération des réalisations
L'outil Simulations géostatistiques gaussiennes permet dans un premier temps de créer une grille de valeurs affectées de façon aléatoire résultant d'une distribution normale standard (moyenne = 0 et variance = 1). Le modèle de covariance (provenant du semi-variogramme spécifié dans la couche de krigeage simple, nécessaire en entrée pour la simulation) est ensuite appliqué au raster. Cela permet de garantir la conformité des valeurs de raster à la structure spatiale du jeu de données en entrée. Le raster résultant constitue une réalisation inconditionnelle et vous pouvez en produire davantage à l'aide d'un raster chaque fois différent de valeurs normalement distribuées. Pour plus d'informations sur cette méthode, lisez l'ouvrage de Dietrich and Newsam (1993).
Si vous avez sélectionné la simulation conditionnelle, les rasters inconditionnels sont conditionnés par krigeage. Ce processus fait appel à l'estimation krigée (prévision) à chaque emplacement pour s'assurer que les valeurs simulées respectent les valeurs des données en entrée et, qu'en moyenne, les prévisions krigées sont répliquées. Pour obtenir plus d'informations sur le conditionnement de réalisations à l'aide du krigeage, consultez l'ouvrage de Journel (1974).
Toutefois, si le modèle de krigeage simple inclut l'erreur de mesure, les valeurs des données en entrée ne seront pas respectées (dans la couche de krigeage simple ou dans les réalisations simulées). En outre, l'outil Simulations géostatistiques gaussiennes a été mis en œuvre pour utiliser un voisinage de recherche continu (ou lisse) qui évite les discontinuités dans les surfaces simulées résultant de variations du voisinage local utilisé dans le processus de krigeage. Pour plus d'informations, reportez-vous aux publications d'Aldworth (1998), et Gribov et Krivoruchko (2004).
Pour plus d'informations sur les concepts de simulation géostatistique et pour obtenir des exemples de simulation conditionnelle et inconditionnelle, consultez la section d'aide sur les concepts clés de la simulation géostatistique.
Dans le cadre d'un workflow général de simulation géostatistique gaussienne, il convient de préparer les données, de créer les réalisations, de restaurer les résultats à l'état des unités d'origine, de procéder au post-traitement des résultats et/ou d'utiliser les résultats en entrée dans une fonction de transfert (modèle) pour évaluer la variabilité de la sortie du modèle. Ce processus est illustré dans la figure suivante :
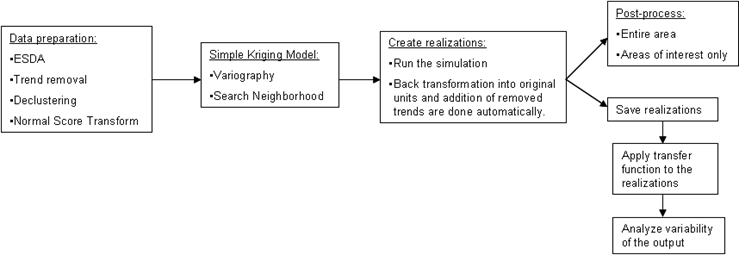
Modèle de krigeage simple pour la simulation
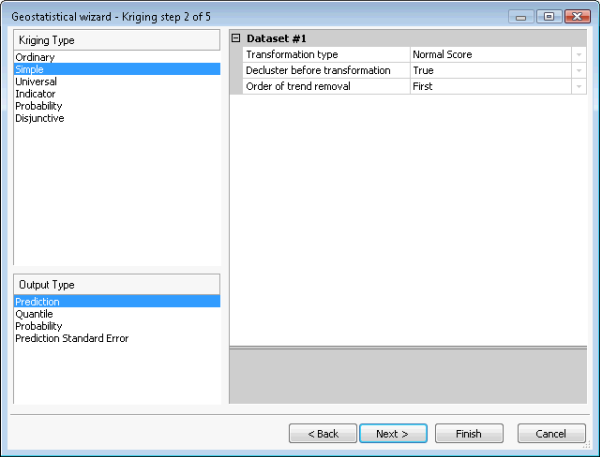
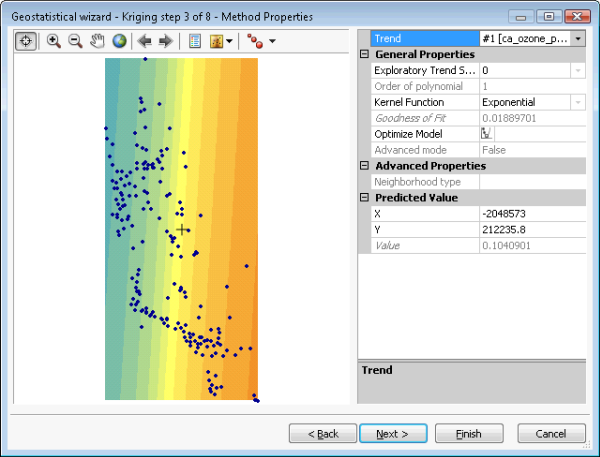
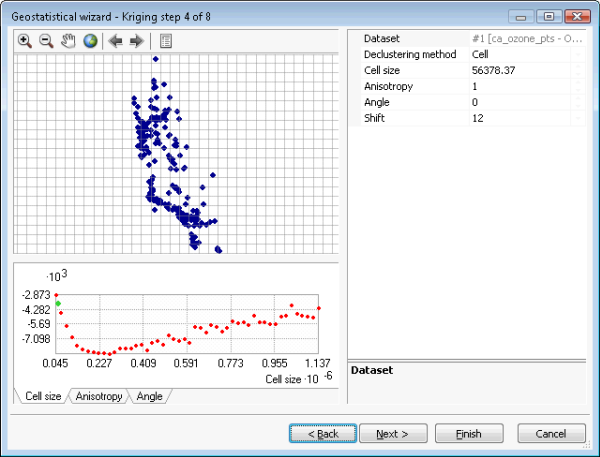
L'outil Simulations géostatistiques gaussiennes accepte tous les modèles de krigeage simple. Toutefois, les résultats de la simulation ne sont valides que si les données en entrée (utilisées pour s'ajuster au semi-variogramme et conditionner les réalisations) sont normalement distribuées. Cela est possible par l'application d'une transformation du score normal. Une désagrégation préalable est nécessaire pour obtenir un histogramme représentatif des données agrégées et les tendances doivent être supprimées pour garantir que la moyenne est stationnaire sur le domaine spatial. Ces étapes sont illustrées dans les figures suivantes. La figure (a) représente un krigeage simple, les options de suppression de tendance, de désagrégation et de transformation du score normal étant sélectionnées. La figure (b) représente la tendance à supprimer du jeu de données avant la désagrégation, la transformation du score normal et la variographie. La figure (c) représente la désagrégation par cellules. La figure (d) représente la transformation du score normal qui utilise dans ce cas la méthode directe.
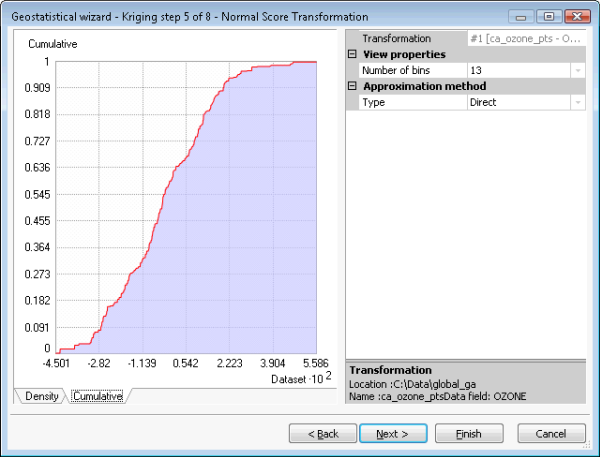
Vérification du résultat de la simulation
Vous devez vérifier les réalisations pour confirmer les points suivants :
- Les valeurs en sortie, leurs modèles spatiaux et les emplacements sont raisonnables.
- L'histogramme des données simulées reproduit en moyenne l'histogramme des données en entrée.
- Les semi-variogrammes des données simulées reproduisent en moyenne le semi-variogramme des données en entrée.
- Dans le cas d'une simulation conditionnelle, les valeurs des données en entrée sont respectées (à moins que le modèle de krigeage simple n'inclue l'erreur de mesure).
Post-traitement
Une fois les réalisations produites, elles font habituellement l'objet d'un post-traitement pour obtenir des récapitulatifs des résultats. L'outil Simulations géostatistiques gaussiennes propose plusieurs options de post-traitement que vous pouvez appliquer sur la totalité de l'étendue spatiale des rasters ou sur des zones présentant un intérêt particulier. Pour définir ces zones, il convient de spécifier une classe d'entités surfaciques dans l'option Entrer des polygones statistiques de l'outil. La sortie est identique dans les deux cas : le post-traitement de la totalité des rasters produit des rasters de synthèse alors que le post-traitement des zones polygonales produit une classe d'entités surfaciques en sortie qui contient des statistiques récapitulatives pour chaque polygone.
Post-traitement de la totalité de l'étendue du raster
- Les rasters en sortie comprennent la valeur minimale générée pour chaque emplacement (cellule), ainsi que les valeurs maximum, moyenne, d'écart type, de premier quartile, médiane (deuxième quartile) et de troisième quartile. Vous pouvez également spécifier un quantile qui doit renvoyer une valeur correspondant à ce quantile, en fonction de la distribution des valeurs simulées pour chaque cellule. Vous pouvez également spécifier une valeur de seuil qui doit renvoyer le pourcentage des valeurs simulées dépassant le seuil pour chaque cellule.
- Vous pouvez limiter l'étendue devant faire l'objet d'un post-traitement en spécifiant un polygone d'emprise ou un ensemble de points (dans ce cas, une enveloppe convexe est générée et utilisée comme polygone d'emprise). Les valeurs ne sont simulées qu'à l'intérieur du polygone d'emprise.
Post-traitement des zones d'intérêt
- Lorsque des zones d'intérêt surfaciques sont spécifiées, la sortie de chaque polygone inclut automatiquement les statistiques récapitulatives décrites dans la table suivante. En outre, vous pouvez spécifier une valeur quantile et une valeur de seuil (comme c'est le cas lors du post-traitement de l'étendue entière du raster). Cette table explique également la sortie générée lorsque vous sélectionnez ces options.
- La sortie récapitulative de ces polygones est calculée à l'aide d'opérateurs semblables à ceux qui sont représentés dans la figure ci-dessous. L'opérateur X utilise toutes les valeurs comprises dans le polygone et calcule une valeur pour chaque réalisation. L'opérateur Y utilise des valeurs de toutes les réalisations. Les valeurs en entrée pour l'opérateur Y sont celles des zones polygonales de chaque réalisation, calculées par l'opérateur X.
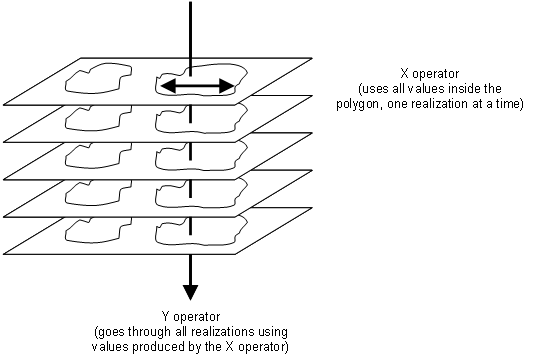
La table suivante explique les champs de la classe d'entités en sortie.
| Nom du champ | Description |
|---|---|
MIN | Valeur minimum d'une cellule quelconque dans toutes les réalisations comprises dans le polygone. |
MAX | Valeur maximum d'une cellule quelconque dans toutes les réalisations comprises dans le polygone. |
MOYENNE | Moyenne de toutes les cellules dans toutes les réalisations comprises dans le polygone. |
STDDEV | Ecart type de toutes les cellules dans toutes les réalisations comprises dans le polygone. |
QUARTILE1 | Valeur du premier quartile de toutes les cellules dans toutes les réalisations comprises dans le polygone. |
MEDIANE | Valeur moyenne de toutes les cellules dans toutes les réalisations comprises dans le polygone. |
QUARTILE3 | Valeur du troisième quartile de toutes les cellules dans toutes les réalisations comprises dans le polygone. |
QUANTILE | Valeur correspondant à un quantile spécifié par l'utilisateur pour toutes les cellules dans toutes les réalisations comprises dans le polygone. |
P_THRSHLD | Pourcentage des cellules dépassant une valeur de seuil spécifiée par l'utilisateur, en fonction de toutes les cellules dans toutes les réalisations comprises dans le polygone. |
X_Y | La fonction X est appliquée aux valeurs des cellules comprises dans le polygone, une réalisation à la fois. Ce processus revient à l'exécution de l'outil Statistiques zonales en utilisant le polygone comme une zone et une réalisation à la fois comme grille de valeurs. La fonction Y est appliquée aux valeurs produites par la fonction X.
|
CELL_COUNT | Nombre de cellules comprises dans le polygone. Si le centre de la cellule est compris dans le polygone, on considère que cette cellule fait partie du polygone. Un nombre négatif indique qu'une partie du polygone ne fait pas partie de l'étendue du raster simulé et/ou qu'une partie du polygone ne fait pas partie de la limite de découpage. Le nombre négatif indique le nombre total de cellules comprises dans le polygone. |
SOURCE_ID | ID de l'entité ou objet de la classe d'entités surfaciques en entrée. |
Pour les options de polygone d'emprise et de zones d'intérêt surfaciques, on suppose que les cellules raster se trouvent à l'intérieur des polygones si le centre de la cellule est à l'intérieur de la limite du polygone.
Exemple de simulation conditionnelle et de résultat en sortie du post-traitement
La figure suivante illustre les résultats d'une simulation conditionnelle avec un post-traitement des polygones sur la sortie. Les cartes indiquent la moyenne et l'écart type de 100 réalisations de valeurs d'ozone pour chaque comté de l'Etat de Californie. Ces valeurs de moyenne et d'écart type pourraient être utilisées par exemple dans le cadre d'études épidémiologiques qui nécessitent la comparaison de l'apparition d'une maladie avec la valeur moyenne d'ozone pour chaque comté.
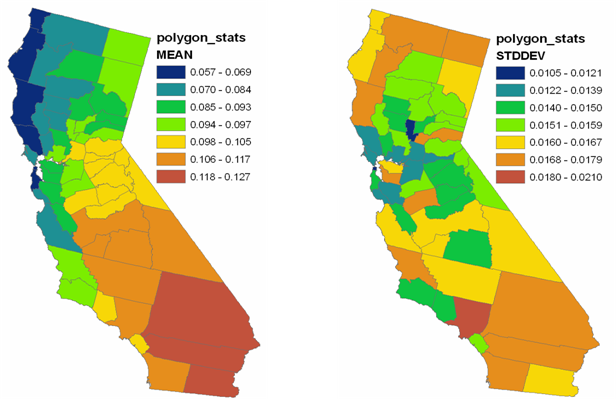
Références et lectures complémentaires
Aldworth, J. 1998. Spatial Prediction, Spatial Sampling, and Measurement Error. Ph.D. Thesis, Iowa State University. 186.
Chiles, J. P., and P. Delfiner. 1999. Geostatistics: Modeling Spatial Uncertainty. New York: John Wiley & Sons, 449–471.
Deutsch, C. V., and A. G. Journel. 1998. GSLIB Geostatistical Software Library and User's Guide, 2nd edition. New York: Oxford University Press, 119–141.
Dietrich, C. R., and G. N. Newsam. 1993. "A Fast and Exact Method for Multidimensional Gaussian Stochastic Simulations." Water Resources Research 29 (8): 2861–2869.
Goodchild, M. F., B. O. Parks, and L. T. Steyaert. 1993. Environmental Modeling with GIS. New York: Oxford University Press, 432–437.
Gribov, A., and K. Krivoruchko. 2004. "Geostatistical Mapping with Continuous Moving Neighborhood." Mathematical Geology 36 (2): 267–281.
Journel, A. G. 1974. "Geostatistics for Conditional Simulation of Ore Bodies." Economic Geology 69: 673–687.
Leuangthong, O., J. A. McLennan, and C. V. Deutsch. 2004. "Minimum Acceptance Criteria for Geostatistical Realizations." Natural Resources Research 13 (3): 131–141.