Que vous considériez la Terre comme une sphère ou un ellipsoïde, vous devez transformer sa surface tridimensionnelle pour créer une feuille de carte plane. Cette transformation mathématique est généralement appelée projection cartographique. Pour comprendre aisément comment les projections cartographiques modifient les propriétés spatiales, il suffit d'imaginer une lumière projetée à travers la terre sur une surface, appelée la surface de projection. Imaginez que la surface de la Terre soit transparente et que le graticule soit tracé dessus. Entourez la terre d'une feuille de papier. Une lumière projetée au centre de la terre reporte les ombres du graticule sur la feuille de papier. A présent, vous pouvez récupérer le papier et le poser à plat. La forme du graticule à plat sur le papier est différente de celle dessinée sur la Terre. La projection cartographique a déformé le graticule.
Un ellipsoïde ne peut être aplati sur un plan, de la même façon qu'une peau d'orange ne peut être aplatie : elle se déchire. La représentation de la surface de la terre en deux dimensions provoque une distorsion de la forme, de la surface, de la distance et de la direction des données.
Une projection cartographique utilise des formules mathématiques pour relier les coordonnées sphériques du globe à des coordonnées planaires plates.
Différentes projections provoquent différents types de distorsions. Certaines projections sont conçues pour minimiser la distorsion d'une ou deux caractéristiques des données. Une projection peut ainsi conserver la surface d'une entité mais en modifier sa forme. Dans le graphique ci-dessous, les données près des pôles sont étirées.
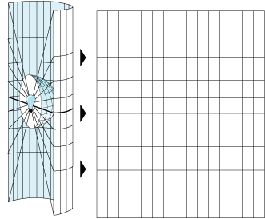
Le diagramme suivant montre comment des entités tridimensionnelles sont comprimées pour s'ajuster à une surface plane.
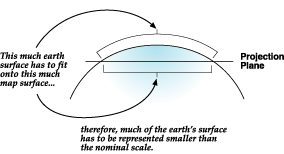
Les projections cartographiques sont conçues pour des usages spécifiques. Une projection cartographique peut être utilisée pour des données à grande échelle sur une surface limitée, alors qu'une autre peut être utilisée pour réaliser une carte du monde à petite échelle. Les projections cartographiques conçues pour les données à petite échelle sont généralement basées sur des systèmes de coordonnées géographiques sphériques plutôt que sphéroïdaux.
projections conformes
Les projections conformes conservent la forme locale. Pour conserver des angles spécifiques décrivant les rapports spatiaux, une projection conforme doit faire apparaître les lignes perpendiculaires du graticule se coupant à un angle de 90 degrés sur la carte. Une projection cartographique y parvient en conservant tous les angles. L'inconvénient est que la surface entourée par une série d'arcs est donc encline à des distorsions importantes. Aucune projection cartographique ne peut conserver les formes de régions plus grandes.
Projections équivalentes
Les projections équivalentes conservent la surface des entités affichées. Pour cela, les autres propriétés (forme, angle et échelle) sont déformées. Dans les projections équivalentes, les méridiens et les parallèles peuvent ne pas se couper à angles droits. Dans certains cas, surtout pour les cartes de petites régions, les formes ne sont pas déformées de façon évidente, et la distinction entre une projection équivalente et une projection conforme est difficile, à moins que des commentaires ou des mesures ne figurent sur la carte.
projections équidistantes
Les cartes équidistantes conservent la distance entre certains points. Aucune projection ne conserve l'échelle correctement sur la totalité d'une carte. Cependant, dans la plupart des cas, l'échelle est conservée correctement sur une ou plusieurs lignes d'une carte. La plupart des projections équidistantes ont une ou plusieurs lignes dont la longueur sur la carte est la même (à l'échelle de la carte) que la longueur de la ligne sur le globe, qu'il s'agisse d'un petit cercle ou d'un grand ou d'une ligne droite ou courbe. Ces distances sont dites vraies. Par exemple, dans la projection sinusoïdale, la longueur de l'équateur et de tous les parallèles est vraie. Dans d'autres projections équidistantes, l'équateur et tous les méridiens sont vrais. D'autres encore (par exemple, la projection équidistante deux points) montrent une échelle vraie entre un ou deux points et chaque autre point de la carte. Rappelez-vous qu'aucune projection n'est équidistante d'un point à l'autre pour tous les points de la carte.
Projections vraies directions
La distance la plus courte entre deux points d'une surface courbe comme la terre se trouve le long de l'équivalent sphérique d'une ligne droite sur une surface plane. C'est-à-dire le grand cercle sur lequel les deux points se trouvent. Les projections à vraies directions, ou azimutales, conservent certains arcs de grands cercles, donnant les directions ou les azimuts de tous les points de la carte correctement par rapport au centre. Certaines projections à vraies directions sont également conformes, équivalentes ou équidistantes.