空間処理では、ジオメトリ関数を使用して入力として空間データを受け取り、データを解析して、出力データを生成します。この出力データは入力データに対して実行された解析によって導きだされます。
入力データから新しいデータを作成する場合は、次の処理を実施できます。
ジオメトリのバッファー
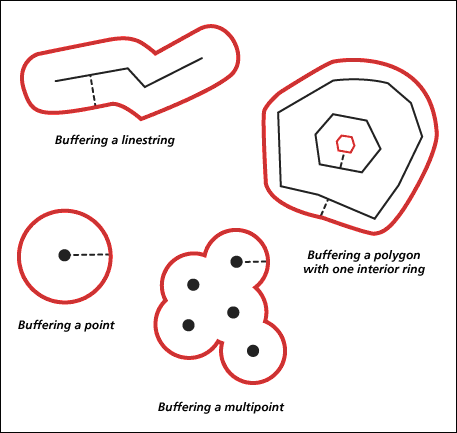
ST_Buffer 関数を実行すると、指定した距離でジオメトリを取り囲むジオメトリが生成されます。1 つのジオメトリをバッファーしたとき、またはコレクションのバッファー ポリゴンが重なり合うのに十分なほど近接している場合には、ポリゴンが 1 つ生成されます。バッファーされるコレクションのエレメント間が十分に離れているときには、それぞれのバッファー ST_Polygons について ST_MultiPolygon が生成されます。
ST_Buffer 関数では、正と負の距離が許容されますが、負の距離のバッファーはディメンションが 2 次元のジオメトリ (ST_Polygon または ST_MultiPolygon) でしか適用できません。バッファー距離の絶対値は、ソース ジオメトリのディメンションが 2 次元よりも小さい場合、つまり、ST_Polygon でも ST_MultiPolygon でもないすべてのジオメトリで使用されます。一般的に、バッファー距離が正の場合は、ソース ジオメトリの中心から遠ざかるポリゴン リングが生成されます。ST_Polygon または ST_MultiPolygon の外部リングについては、距離が負の場合は中心に近づくように生成されます。ST_Polygon または ST_MultiPolygon の内部リングについては、バッファー距離が正であればバッファー リングが中心に向かって生成され、負であれば中心から遠ざかるように生成されます。バッファー処理では、重なり合うバッファー ポリゴンがマージされます。負の距離がポリゴンの最大内幅の半分よりも大きい場合は、空のジオメトリになります。
構文と例については、「ST_Buffer」をご参照ください。
凸包
ST_ConvexHull 関数は、3 つ以上の頂点を持ち凸を形成するジオメトリの凸包ポリゴンを返します。ジオメトリの頂点が凸を形成しない場合、ST_ConvexHull は NULL を返します。たとえば、2 つの頂点で構成される線上で ST_ConvexHull を使用すると、NULL が返されます。同様に、ポイント フィーチャに ST_ConvexHull 操作を使用した場合にも、NULL が返されます。一連のポイントを隣接させて TIN (Triangulated Irregular Network) を作成する場合には、通常、凸包の作成が最初のステップになります。
構文と例については、「ST_ConvexHull」をご参照ください。
ジオメトリの違い
ST_Difference 関数を使用すると、第 2 のジオメトリが交差しない第 1 のジオメトリ部分が返されます。つまり、空間の論理的な AND NOT です。ST_Difference 関数は同じディメンションのジオメトリだけを対象とし、ソース ジオメトリと同じディメンションをもつコレクションを返します。複数のソース ジオメトリが同等の場合は、空のジオメトリが返されます。 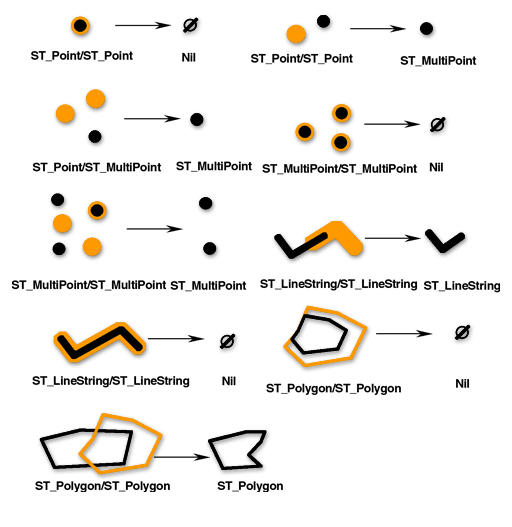
構文と例については、「ST_Difference」をご参照ください。
ジオメトリの交差
ST_Intersection 関数を使用すると、2 つのジオメトリの交差セットが返されます。この交差セットは、必ず、ソース ジオメトリの最小ディメンションであるコレクションとして返されます。たとえば、ST_Polygon に交差する ST_LineString に ST_Intersection 関数を使用すると、ST_Polygon の内部と境界に共通する ST_LineString の部分が ST_MultiLineString として返されます。ソースの ST_LineString が 2 つ以上の不連続のセグメントで ST_Polygon に交差する場合には、ST_MultiLineString に 2 つ以上の ST_LineString が格納されます。交差していないジオメトリの場合や、交差によって両方のソース ジオメトリよりも小さいディメンションとなる場合は、空のジオメトリが返されます。以下に ST_Intersection 関数の例をいくつか図で説明します。
ジオメトリの対称差
ST_SymmetricDiff 関数は、2 つのジオメトリの対称差を返します。つまり、これは空間の論理 XOR です。ソース ジオメトリは同じディメンションでなければなりません。ST_SymmetricDiff 関数は、ジオメトリが等しければ空のジオメトリを返します。それ以外の場合、この関数はコレクションとして結果を返します。
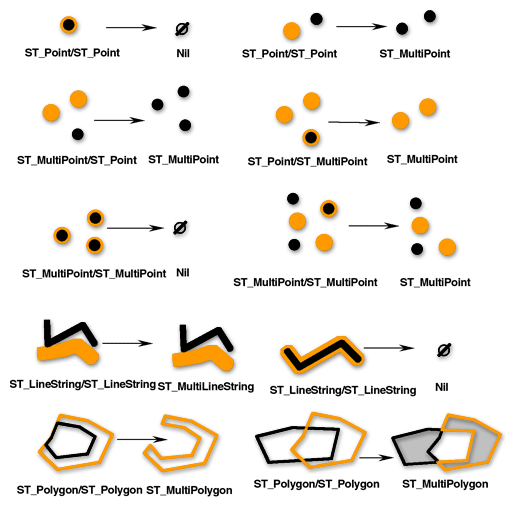
構文と例については、「ST_SymmetricDiff」をご参照ください。
ジオメトリの和 (ユニオン)
ST_Union 関数は、2 つのジオメトリのユニオン セットを返します。これは空間の論理 OR です。ソース ジオメトリは同じディメンションでなければなりません。ST_Union では、結果が必ずコレクションとして返されます。
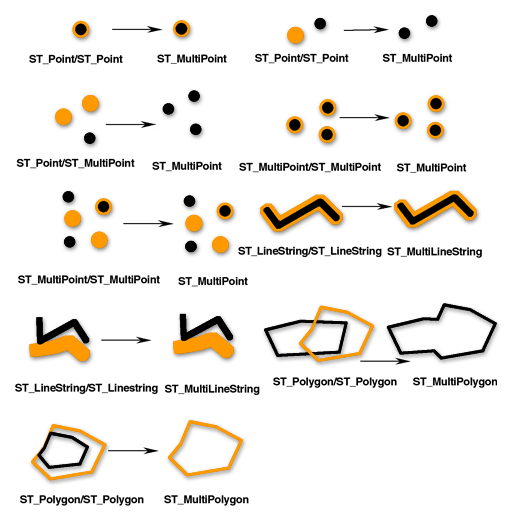
構文と例については、「ST_Union」をご参照ください。
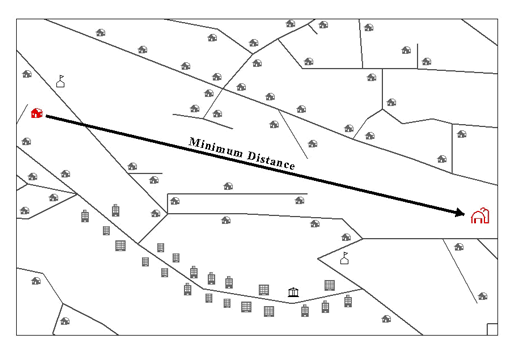
最短距離
これまでの関数は、新しいジオメトリを返すものでした。ST_Distance 関数は、2 つのフィーチャを入力として受け取り、それらの間の最短距離を返します。
離れたフィーチャの最短距離は、2 つの位置の間の (直線距離としての) 最短距離を表します。たとえば、ある地点から別の地点まで運転する場合の移動距離ではなく、地図上の 2 つの位置間に直線を引いた場合に計測される距離です。ST_Distance 関数では、2 つの離れたジオメトリの最短距離が返されます。ジオメトリが離れていない (つまり、一致している) 場合にこの関数を使用すると、最短距離としてゼロが返されます。
集約
集約処理は、ジオメトリのコレクションに対して実行した分析結果として 1 つのジオメトリを返します。ST_Aggr_ConvexHull 関数は、各入力ジオメトリの凸包ポリゴンで構成されるマルチポリゴンを返します。頂点が 3 つに満たない入力ジオメトリには凸包がありません。すべての入力ジオメトリで頂点が 3 つに満たない場合に ST_Aggr_ConvexHull を使用すると、NULL が返されます。
ST_Aggr_Intersection 関数は、すべての入力ジオメトリの交差の集約である 1 つのジオメトリを返します。クエリによって、交差する多数のフィーチャが見つかることがあります。ST_Intersection 演算子を使用すると、各ジオメトリ セットの交差を表す複数のフィーチャが返されます。たとえば、線とポイント フィーチャクラスの交差がある場合は、各交差について ST_Point ジオメトリが 1 つ返されます。
代わりに ST_Aggr_Intersection を使用すると、ジオメトリ コレクションが 1 つ返されます。たとえば、前述の線とポイント フィーチャクラスの交差を表す 1 つのジオメトリを求める場合は、ST_Aggr_Intersection を使用することで、すべての交差ポイントで構成される 1 つの ST_MultiPoint ジオメトリが返されます。1 つのポイントと 1 本の線だけしか交差していない場合には、ST_Point ジオメトリが返されます。
ST_Aggr_Intersection では複数のジオメトリの交差を特定できるのに対し、ST_Intersection では、2 つのジオメトリの間での交差しか特定できません。たとえば、特定の校区、電話サービス、高速インターネット プロバイダーなど、いくつかの特定のサービスの対象となっており、特定の委員が代表者となっている物件を検索する場合は、それらすべての領域の交差を特定する必要があります。それらの領域の 2 つだけについて交差を特定しても、必要なすべての情報を得ることはできないため、同じクエリですべての領域を評価できるよう sde.ST_Aggr_Intersection 関数を使用します。
ST_Aggr_Union 関数を使用すると、提供したすべてのジオメトリの和 (ユニオン) である 1 つのジオメトリが返されます。各入力ジオメトリはタイプが同じである必要があります。たとえば、ST_LineStrings と ST_LineStrings の和や、ST_Polygons と ST_Polygons の和を取得することはできますが、ST_LineString フィーチャクラスと ST_Polygon フィーチャクラスの和を取得することはできません。通常、集約ユニオンにより得られる結果はコレクションです。たとえば、空いているすべての 0.5 エーカー未満の土地区画の集約ユニオンを求める場合には、この条件を満たすすべての土地区画が隣接している場合を除き、ジオメトリとしてマルチポリゴンが返されます。すべての土地区画が隣接している場合は、1 つのポリゴンが返されます。