Spatial Analyst のライセンスで利用可能。
3D Analyst のライセンスで利用可能。
逆距離加重 (Inverse Distance Weighted: IDW) 内挿は、線形的に加重されたサンプル ポイント セットを組み合わせることによってセル値を求めます。この場合の重みは距離に反比例します。内挿されるサーフェスは位置的な従属変数です。
この方法では、マップされる変数の影響は、サンプル位置からの距離が遠くなるにつれて小さくなると仮定されています。たとえば、小売サイトの解析で消費者の購買力のサーフェスを内挿する場合、消費者は家に近い店舗で購入する傾向が高いので、距離が遠いほど購買力の影響が小さくなります。
乗数パラメーターによる影響力の制御
IDW では、距離の逆数を累乗して影響力を求めます。[乗数] パラメーターを使用すれば、出力ポイントまでの距離に基づいて、内挿値に対する既知のポイントの有意性を制御できます。乗数は正の実数であり、デフォルト値は 2 です。
乗数として大きい値を指定するほど、最近隣ポイントに重点が置かれます。つまり、近傍データの影響力が最も大きく、サーフェスの詳細度が高くなります (滑らかさが低下します)。乗数を大きくすると、内挿値が最近隣サンプル ポイントの値に近づきます。小さい乗数値を指定すると、より遠くにある周辺ポイントまで影響がおよび、スムーズなサーフェスが得られます。
IDW 数式は実際の物理プロセスに関連付けられていないので、使用する乗数値が大きすぎるかどうかを判断する方法がありません。1 つの目安として、乗数 30 は極端に大きいと見なされており、通常は使用しません。また、距離または乗数値が大きいと、正しい結果が得られない可能性があります。
最小平均絶対誤差が最も小さくなる場合が最適な乗数値と見なされます。ArcGIS Geostatistical Analyst エクステンションには、これを検証するためのツールが用意されています。
内挿で使用するポイントの制限
内挿サーフェスの特性を制御するには、各出力セル値の計算で使用する入力ポイントを制限する方法もあります。対象となる入力ポイントの数を制限すると処理速度が向上します。また、予測対象のセル位置から遠い入力ポイントは、空間的相関がほとんどない (またはまったくない) 可能性があります。そのような入力ポイントは計算から除外してかまいません。
使用するポイントの数を直接指定するか、希望の半径を指定し、その半径内にあるポイントを内挿対象とすることもできます。
可変の検索半径
可変の検索半径では、内挿セルの値の計算に使用するポイント数が指定されます。これにより、各内挿セルについて、指定した入力ポイント数に達するまでに必要な検索半径の長さに合わせて、半径距離が変化します。したがって、内挿セルの近くにある計測ポイントの密度により、小さい近傍も大きい近傍もあります。また、検索半径の上限となる最大距離 (マップの単位) も指定できます。指定したポイント数を取得する前に、ある近傍の半径が最大距離に達した場合、その位置の推定は、最大距離内にある計測ポイント数で実行されます。一般的に、現象の変化が多様である場合は、近傍、または最小ポイント数を小さくします。
固定の検索半径
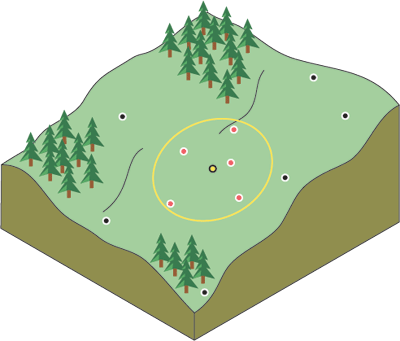
固定の検索半径には、近傍距離と最小ポイント数が必要です。距離は、近傍の円の半径 (マップの単位) を示します。半径の距離が一定なので、内挿する各セルについて、入力ポイントの検出に使用する円の半径は同じです。最小ポイント数は、近傍内で使用される計測ポイントの最小数です。半径内にある計測ポイントがすべて、各内挿セルの計算に使用されます。近傍内の計測ポイントの個数が、指定した最小値よりも小さい場合は、最小ポイント数に達するまで検索半径が増加されます。解析エリアの各内挿セル (セル中心) について、指定された固定検索半径が使用されます。したがって、計測ポイントが均等に広がっていない場合 (均等な場合はまれ)、推定には、異なる近傍で異なる計測ポイント数が使用されることになります。
バリアの使用
バリアとは、入力サンプル ポイントの検索を制限するブレークラインとして使用されるポリライン データセットです。ポリラインは、崖、尾根、その他の地形の分断を表すことができます。バリアに対して、現在の処理セルと同じ側にある入力サンプル ポイントのみが、処理対象になります。
参照
Philip, G. M., and D. F. Watson. "A Precise Method for Determining Contoured Surfaces." Australian Petroleum Exploration Association Journal 22: 205–212. 1982.
Watson, D. F., and G. M. Philip. "A Refinement of Inverse Distance Weighted Interpolation." ジオプロセシング 2:315–327. 1985.