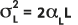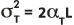ArcMap

多孔質媒体内の分散 (Porous Puff)の仕組み

Spatial Analyst のライセンスで利用可能。

多孔質媒体における溶質移動は、主に移流と水力学的分散の 2 つの作用によります。移流とは、搬送流体による溶質の受動的な移動です。分散とは、間隙における流体の移動速度の差により、溶質が流体と混合することです。[多孔質媒体内の分散 (Porous Puff)] ツールは、帯水層が垂直方向に混合されていると仮定します。つまり、垂直なセクション全体で濃度が一定です。これにより、ラスター データ モデルで必要とされるように、2 つの次元で数学モデルを適用できます。

2 次元分散

多孔質媒体における 2 次元分散は、縦方向 (流向方向) の項 XL と横方向 (流向方向に垂直な方向) の項 XT を持つ移流分散方程式 (Bear, 1979; Freeze and Cherry, 1979; and Marsily, 1986) で、次の式のように表されます。

移流分散方程式

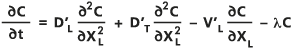
  • ここで、

    C: 2 つの空間次元と時間 t の関数として表される溶質濃度。

    ∂C/∂t: 時間微分を表します。

    D'L: 縦方向の有効 (遅延) 分散係数。

    D'T: 横方向の有効 (遅延) 分散係数。

    λ: 減衰係数 (一次指数減衰の定数と仮定)。

分散係数

分散係数は、溶質が指定方向に広がる程度の尺度であり、次の式で表されます。

D'i = Di/R

  • ここで、

    R: 遅延係数。

    i: 方向 (縦または横)。

分散係数は、特定媒体での溶質の挙動に関係があります。

分散度と分散係数の関係

分散度 αL(縦方向の分散度) と αT(分散度の比から得られた横方向の分散度) は、分散係数と次の式のような関係にあります。

D'L = αL V' および

D'T = αT V'

  • ここで、

    V': 溶質の平均遅延速度。

    XL: 縦方向 (質量中心における流向方向と平行) の変位。

    XT: 横方向 (質量中心における流向方向と垂直) の変位。

    V'L: 縦方向の溶質の遅延速度。

移動速度

地下水流では次の式が成り立ちます。

V = q / n

  • ここで、

    q: Darcy 流束 (単位断面積あたりの流出量)。

    n: 地層の有効間隙率。

V' = V / R

移動速度の詳細については、ダルシー流速 のドキュメントをご参照ください。

ガウス分散

[多孔質媒体内の分散 (Porous Puff)] ツールで使用されるこの方程式の近似解は、初期濃度 0 (垂直方向に混合された帯水層) の 2 次元領域における瞬間的なポイント ソースからの分散はガウス分布に従うという前提に基づき、次の式で計算されます。

ポイント ソースのガウス 2 次元分散を前提とする方程式

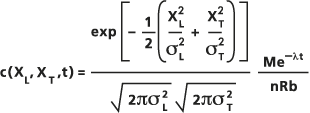
  • ここで、

    M: 瞬間的にソースから放出された溶質の質量 (質量単位)。

    n: 帯水層の間隙率。

    R: 遅延係数。

    b: 帯水層の厚さ (長さ単位)。

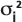    ガウス分散の分散度: 縦方向の分散度、ユーザー指定の分散度の比、およびトラック ファイルから得られる溶質の質量中心の移動パスの長さの関数として決定される縦方向と横方向のガウス分布の分散。

この 2 変数ガウス分布関数の一般的な楕円形状を以下の図に示します。

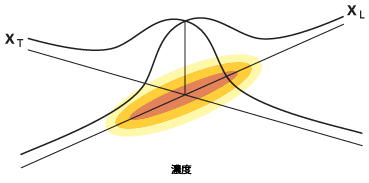
2 変数ガウス分布の形状
2 変数ガウス分布の形状

[多孔質媒体内の分散 (Porous Puff)] ツールの解には、いくつかの注意すべき制限と前提があります。分散の楕円の中心は溶質の質量中心で、入力ファイルに記述されたフロー軌跡に沿って移動すると仮定されます。同様に楕円の向きはフロー軌跡に対して固定され、重心の位置で長軸は軌跡に垂直です。分散に寄与する間隙率と層厚はそれぞれのラスターの重心位置から内挿され、周囲のセルからの情報は使用しません。遅延、時間、減衰係数、縦方向の分散度、および分散度の比は、定数としてユーザーが指定します。

分散度

分散度は、多孔質媒体を通過する溶質の分散を支配するパラメーターで、長さの単位で指定します。[多孔質媒体内の分散 (Porous Puff)] ツールのモデルでは、上記のガウス分布の分散式で分散 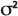ガウス分散の分散のシンボル を計算するために使用する分散度は、次の式で得られます。

  • 縦方向の分散
  • 横方向の分散

分散度の性質とその特定方法は、地下水のモデル化のコミュニティにおいて関心が高く論争のある話題であり、汎用的に受け入れられている計算方法はありません。さまざまな地層の分散度に関する考察が、Gelhar らの文献 (1992) に記載されています。

次のグラフは発表された文献からさまざまなデータをまとめたもので、縦方向の分散度と、着目する問題のスケール、つまりソースの位置から観測点までの距離との関係を示します。

スケールの関数としての分散度の値

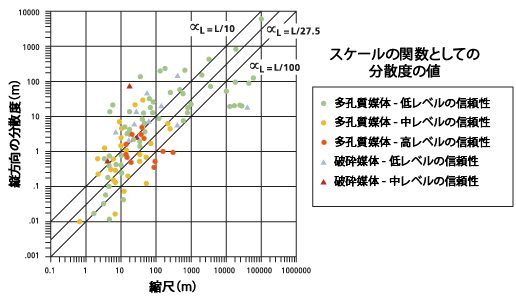
  • グラフの実線 (中央の線) は、[多孔質媒体内の分散 (Porous Puff)] ツールで計算した縦方向の分散度のデフォルト値です。

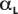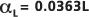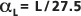    この実線は、縦分散度のシンボル と L との関係を線形回帰近似して得られ、その結果として 線形回帰近似して得られた実線(つまり 分子として表される線形回帰近似して得られた実線) が得られます。移動パス L の長さが観測スケールです。

    この回帰に使用した統計情報の凡例も示されています。比較のために、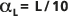L/10 の回帰ライン と L/100 の回帰ライン が破線 (外側の線) で示されています。

このような汎用近似の妥当性を否定している研究者もいるので、このデフォルト計算は、参考としてのみ使用すべきです。特定のスケールやサイトでは、有効な分散度の上限と下限の差が 2 桁違う場合もあり、信頼できる推定値は低い値になる傾向があります。理論的な根拠のないデフォルト値を使用するのではなく、分散度の範囲を使用してシミュレーションを複数回実行する必要があります。複数の結果を検討することは、1 回のシミュレーション結果を使用するよりも妥当性が高くなります。

以下の図に示す、横方向の分散度に対する縦方向の分散度の比の推定についても、同様の注意が当てはまります。これらの値の関係は一般的に単なる比ですが、ここでも値の範囲を使用して試験する必要があります。

分散度の比較

縦方向の分散度と横方向の分散度の比較

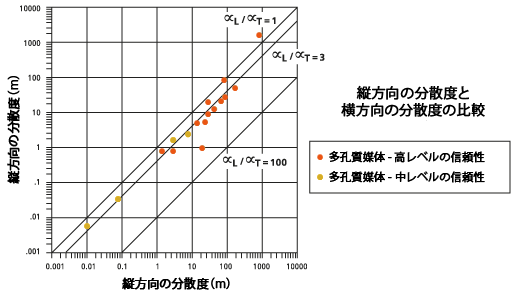
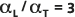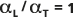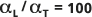以下の図に、デフォルトの分散度の比 デフォルトの分散度の比 を実線 (中央の線) で示します。比較のために、分散度の比 = 1 と 分散度の比 = 100 が破線 (外側の線) で示されています。

有効な間隙率と透水率の値

Gelhar et al は、有効な間隙率と透水率の値を表にまとめています。これらの値の表は、Freeze と Cherry (1979)、および Marsily (1986) の文献にも記載されています。

遅延

遅延とは、搬送流体の速度と溶質の速度との比で、1 ～∞の数値で表され、単位はありません。遅延の値 2 は、多孔質媒体を溶質が浸透流速の半分の速度で移動することを示します。理想的なトレーサは吸着せず、流体と共に溶液内を移動します。このような溶質の遅延値は 1 で、搬送流体と同じ速度で移動します。

この現象は、多孔質マトリックスに対する成分の吸着と脱着の結果で、特に多孔性の壁の有機塗装に見られます。遅延の方程式は、Freeze と Cherry の文献 (1979) の考察に次の式で示されています。

遅延の方程式

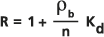
  • ここで、

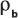    行列の仮比重 : 行列の仮比重。

    n: 地層の間隙率。

    Kd: 線形等温線を仮定したときに、液相と固相との間で発生する溶質の高速の可逆吸着による分割を表す分配係数。

Marsily (1986) も、遅延係数と吸着について、詳しい考察を行っています。

移流分散モデリングの実行

[ダルシー フロー (Darcy Flow)] ツール、[粒子追跡 (Particle Track)] ツール、および [多孔質媒体内の分散 (Porous Puff)] ツールは、地下水成分の基本的な移流拡散モデリングを実行するために使用できます。[ダルシー フロー (Darcy Flow)] ツールは地質データから流速域を生成し、[粒子追跡 (Particle Track)] ツールはポイント ソースから流域にわたる移流のパスをたどり、[多孔質媒体内の分散 (Porous Puff)] ツールは流路に沿って移流する際の成分の瞬間ポイント リリースの流体分散を計算します。

これらのツールを用いる移流分散のモデル化に関する詳細な考察が、Tauxe (1994) の文献に記載されています。

一般的に、地下水モデリングにおいては、[ダルシー フロー (Darcy Flow)] ツール、[粒子追跡 (Particle Track)] ツール、[多孔質媒体内の分散 (Porous Puff)] ツールの順に実行します。

例

  • [多孔質媒体内の分散 (Porous Puff)] ツールのダイアログ ボックスの例を次に示します。

    入力粒子トラック (particle track) ファイル: ttrack.txt

    入力有効地層間隙率 (effective formation porosity) ラスター: poros

    入力飽和帯水層厚 (saturated thickness) ラスター: thickn

    出力ラスター: ppuff1

    質量: 3.2e7

    拡散時間: 50000

    縦分散度: 6

    拡散率: 3

    遅延係数: 1

    減衰係数: 250

  • マップ代数演算での [多孔質媒体内の分散 (Porous Puff)] ツールの使用例は、次のとおりです。 
    outPPuff1 = PorousPuff(ttrack.txt, poros, thickn, 1000000, 0.01, 10, 1.5, 1.0, 500)
  • 3 種類の地下水モデリング ツールを使用するマップ代数演算式の順序は、次のとおりです。
    out_vol = DarcyFlow(head, poros, thickn, transm, dir1, mag1)
ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, "#", "#", track_feat.shp)
out_puff = PorousPuff(ttrack.txt, poros, thickn, 3.2e7, 50000, 6, 3, 1, 250)

参照

Bear, J. 1979, Hydraulics of Groundwater. McGraw-Hill.

Freeze, R. A., and J. A. Cherry. 1979. Groundwater. Prentice–Hall.

Gelhar, L. W., C. Welty, and K. R. Rehfeldt. 1992. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research 28 (7): 1955-1974.

Marsily, G. de. 1986. Quantitative Hydrogeology. Academic Press.

Tauxe, J. D. 1994. "Porous Medium Advection–Dispersion Modeling in a Geographic Information System". Ph.D. diss., University of Texas, Austin.

関連トピック