通过聚合点创建时空立方体工具获取时间戳点要素,然后通过将点聚合到时空条柱来将其构建为 netCDF 数据立方体。在每个条柱内计算点,计算所有汇总字段统计数据并使用 Mann-Kendall 统计测量每个位置的跨时间的条柱值趋势。您极可能会使用此工具来创建进行进一步空间-时间模式挖掘时所需的输入立方体,而且还会使用此工具来检查整个研究区域的时间序列趋势。
分析结果
此工具的输出是表示输入点的 netCDF。可使用 ArcGIS Pro 将 2D 或 3D 立方体点计数数据可视化。除了 netCDF 文件以外,还可将汇总了时空立方体尺寸和内容的消息写到结果窗口中。右键单击结果窗口中的消息条目并选择查看,将在消息对话框中显示结果。

立方体结构将具有行、列和时间步长。如果将行数乘以列数和时间步长数,则将得到立方体中的条柱总数。行和列可确定立方体的空间范围,而时间步长则可确定时态范围。
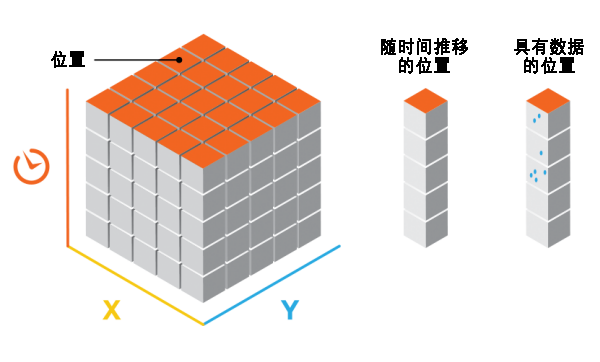
对于大多数分析来说,只有包含至少一个时间步长间隔的数据的位置才会被包括在分析中,但这些位置将在所有时间步长中进行分析。计算点计数时,对于任何没有点的条柱假设计数为零,但关联的位置在至少一个时间步长间隔内具有至少一个点。如果位置具有至少一个时间步长间隔的数据,则与位置相关的零的百分比信息将被在消息中报告为稀少。计算汇总字段的值时,通过参数填充空条柱将确定没有点的条柱的填充方式。任何无法根据估算条件进行填充的条柱都将导致整个位置从分析中排除。使用空间相邻要素的平均值至少需要 4 个相邻要素来填充空条柱,使用时间空间相邻要素的平均值至少需要 13 个相邻要素来填充空条柱。
输出消息的末尾具有总体数据趋势信息。此趋势基于非时空序列分析。其所回答的问题为:随着时间的推移,输入点所表示的事件在总体上有所增加还是有所减少? 要获得答案,可使用 Mann-Kendall 统计将每个时间步长间隔中所有位置的点数作为计数值的时间序列进行分析。
聚合的条柱维度
多数情况下,您将了解如何定义立方体条柱维度,强烈建议您考虑您要回答的特定问题所应采用的适合维度。例如,如果您正在查看犯罪事件,您可能决定将点聚合到 400 米或 0.25 英里的条柱中,因为那是您城市街区的尺寸。如果您具有整整一年的数据,则可能决定查看每月或每周事件聚合的趋势。
默认参数
在少数情况下,如果您对于使用任何特定时间步长间隔或距离间隔没有强大的理由,则可将时间步长间隔或距离间隔参数留空并让工具为您计算默认值。
默认条柱距离的计算方式如下:
- 确定输入要素范围(最大范围)的最长边的距离。
- 条柱距离为最大范围除以 100 的值,或根据输入要素空间分布算法得出值中较大的一个。
默认时间步长间隔基于用于确定时间步长间隔的最佳数量和宽度的两种不同算法。这些算法的大于 10 的最低数值结果用于默认时间步长间隔数。如果两个数值结果均小于 10,则 10 将变为默认时间步长间隔数。
时间步长对齐
在将数据聚合到时空立方体中时,需要考虑时间步长对齐这一重要参数,因为它能够确定聚合的开始和结束位置。让我们来了解一个示例。
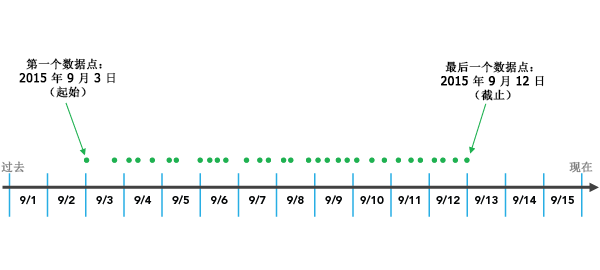
结束时间
例如,如果选择了时间步长间隔为 3 天的 END_TIME 时间步长对齐,分组将使用最后的数据点启动并以 3 天的时间增量向后开始聚合,直到所有数据点落在同一时间步长中为止。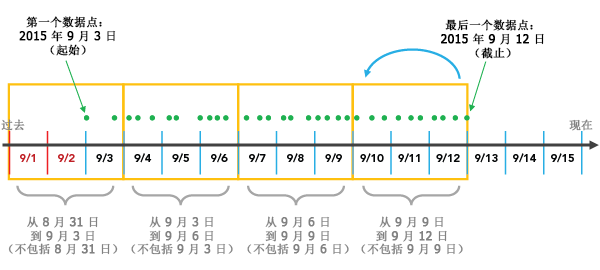
要特别注意,根据所选的时间步长间隔,可在立方体的开始处创建在其整个时间跨度中不具有数据的时间步长。在上面的示例中,您会注意到尽管 9/3 之前没有数据,9/1 和 9/2 仍被纳入到了第一个时间步长中。这些空的日期是时间步长的一部分,但却不存在与其相关的数据。这可能会使结果产生偏差,因为存在时间偏差的时间步长内的点将显著少于其他时间步长内的点,而这实际上是聚合方案造成的人为结果。报告指示第一个或最后一个时间步长中是否存在时间偏差。在本例中,第一个时间步长中的三天中有两天不存在数据,所以时间偏差为 66%。
由于许多分析关注的是最近发生的事情,所以时间步长对齐的默认选项是END_TIME,因此最好将此偏差放到立方体的开始位置。另一个解决方案能够彻底避免出现时间偏差,可提供按时间步长间隔均匀分割的数据,因此时间段就不会出现偏差了。要完成此操作,您可以创建一个数据选择集,其中排除落在您所希望的第一个时间段之外的点数据集。在本示例中,选择所有未落在 9/4 之前的数据即可解决此问题。报告显示第一个和最后一个时间步长的时间跨度以及用于确定数据中断位置的信息。
另外要特别注意,在向后推移时间的过程中,如果最后的条柱恰好落在了作为起始点的第一个数据点上,则最后的数据点将不会被纳入到该条柱中。这是因为对于 END_TIME 时间步长对齐,每个条柱都包括了给定条柱中的最后日期,虽时间可向后推移却不会包括该条柱中的第一个日期。因此,在这种情况下,需要添加附加的条柱以确保第一个数据点能够被纳入其中。
开始时间
例如,如果选择了时间步长间隔为 3 天的 START_TIME 时间步长对齐,分组将使用最后的数据点启动并以 3 天的时间增量向后开始聚合,直到所有数据点落在同一时间步长中为止。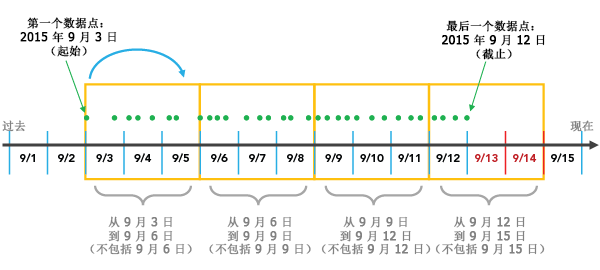
有一些重要的事情需要注意。其中一项是针对基于所选时间步长间隔的 START_TIME 时间步长对齐,可在时空立方体的结束处创建在其整个时间跨度中不具有数据的时间步长。在上面的示例中,您会注意到尽管 9/12 之后没有数据,9/13 和 9/14 仍被纳入到了最后一个时间步长中。这些空的日期是时间步长的一部分,但却不存在与其相关的数据。这可能会使结果产生偏差,因为存在时间偏差的时间步长内的点将显著少于其他时间步长内的点,而这实际上是聚合方案造成的人为结果。报告指示第一个或最后一个时间步长中是否存在时间偏差。在本例中,最后一个时间步长中的三天中有两天不存在数据,所以时间偏差为 66%。在选择 START_TIME 时间步长对齐时问题尤为严重,这是因为侧重于最近数据的分析会显著受到影响。解决方案是提供由时间步长间隔均匀分割的数据,因此时间段就不会出现偏差了。要完成此操作,您可以创建一个数据选择集,其中将排除落在您所希望的最后一个时间段之外的点数据集。在本示例中,选择所有未落在 9/11 之后的数据即可解决此问题。还可以选择从数据集的起点去掉 2 天,这也会使数据均匀分布到时间步长中。报告显示第一个和最后一个时间步长的时间跨度以及用于确定数据中断位置的信息。
另外要特别注意,在向前推移时间的过程中,如果最后的时间步长恰好落在了作为结束点的最后一个数据点上,则最后的数据点将不会被纳入到该条柱中。这是因为对于 START_TIME 时间步长对齐,每个条柱都包括了给定条柱中的第一个日期,虽时间可向前推移却不会包括该条柱中的最后一个日期。所以在这种情况下,需要添加附加的条柱以确保最后一个数据点能够被纳入其中。
参考时间
REFERENCE_TIME 时间步长对齐能够确保特定日期可对立方体中某一时间步长的开始或结束时间进行标记。
在选择落在数据集范围之后、位于最后的数据点或位于数据集中间的 REFERENCE_TIME 时,会将其视为某一时间步长的最后一个数据点,所有其他位于任何一侧的条柱将使用时间步长对齐进行创建,直到覆盖所有数据为止,如下图所示。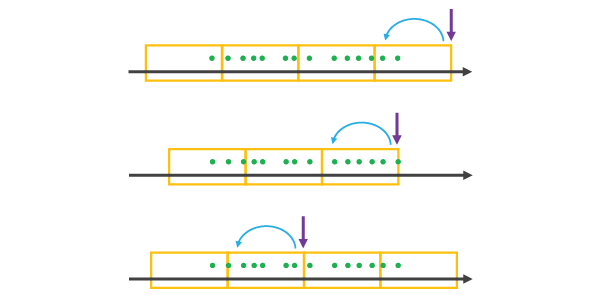
在选择落在数据集范围之前或位于最开始的数据点的 REFERENCE_TIME 时,会将其视为某一时间步长的第一个数据点,所有其他位于任何一侧的时间步长将使用 START_TIME 时间步长对齐进行创建,直到覆盖所有数据为止,如下图所示。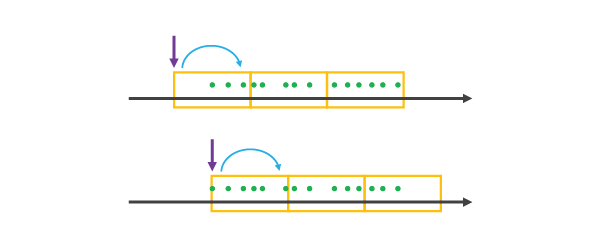
请注意,选择数据范围之前或之后的REFERENCE_TIME可能会创建为空或部分为空的条柱,这会对您的分析造成偏差。
模板立方体
通过选择使用模板立方体,您能够在分析不同的数据集时使用一致的空间范围和时间步长间隔。例如,您可以在获得了下一年的数据时,使用上一年的时空立方体作为模板立方体,这能够确保所使用的空间范围和时间步长间隔的一致性,并同时使立方体得到扩展以覆盖新数据。您也可以将一种事件类型的时空立方体用作分析另一种事件类型的模板立方体,从而确保对分析结果的比较是有效的。
选择使用模板立方体可对时间步长对齐产生影响。让我们来了解几个示例。在选择一个落在输入要素时间跨度之前或之后的模板立方体时,将使用模板立方体的时间步长对齐添加时间步长,直到时间步长覆盖所有数据为止。所得的时空立方体将在模板立方体与输入要素在时间上不重叠的位置存在空立方体。这会对分析结果造成偏差。如果模板立方体与输入要素重叠,则所得的时空立方体将覆盖模板立方体的时态范围,并使用模板立方体的时间步长对齐进行扩展,直到覆盖所有输入要素为止。下图以蓝色显示模板立方体,而以橙色显示所得的时空立方体。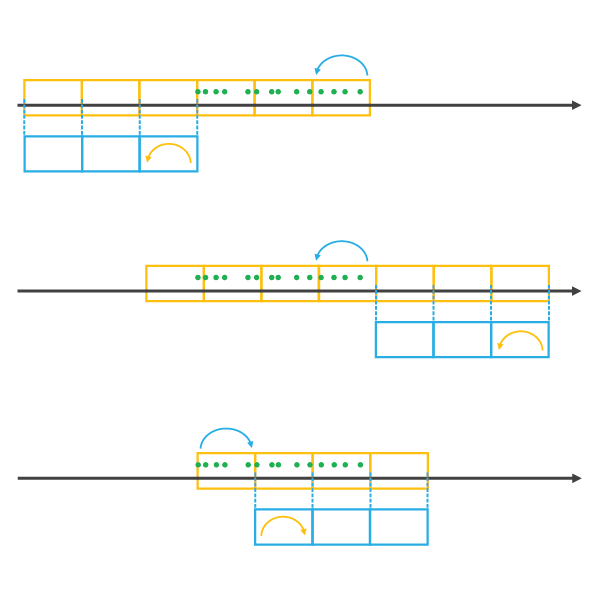
要特别注意,在使用模板立方体创建新的时空立方体时,模板立方体的时间范围将得到扩展,直到覆盖所有数据为止。这样您便可以使用上一年的立方体,来创建包括上年数据和本年数据的新立方体。将采取其他方式处理模板立方体的空间范围。不会对落在模板立方体的空间范围之外的任何数据进行分析。模板立方体和所得的时空立方体将拥有相同的空间范围。如果在创建模板立方体时出现了不应出现的新要素,则只能在空间范围内出现变化,其中空间范围内之前没有数据的位置会出现数据。
趋势分析
在每个带有数据的位置上,将 Mann-Kendall 趋势测试作为独立的条柱时间序列测试加以执行。Mann-Kendall 统计是条柱计数或值及其时间序列的等级相关分析。将第一个时间段的条柱值与第二个时间段的条柱值进行比较。如果前者小于后者,则结果为 +1。如果前者大于后者,则结果为 -1。如果二者相等,则结果为 0。对每对时间段的比较结果进行求和。预期的总和为 0,表示随着时间的推移,值中不存在趋势。基于条柱时间序列中值的方差,将关联数、时间段数、观察的总和与预期总和 (0) 进行比较,以确定差异是否具有统计显著性。每个条柱时间序列的趋势将被记录为 z 得分和 p 值。小 p 值表示趋势具有统计显著性。与 z 得分相关联的符号可确定趋势是条柱值增加(正 z 得分)还是条柱值减少(负 z 得分)。对趋势结果进行可视化的策略将在可视化时空立方体中进行提供。
其他资源
时空立方体的创建、可视化和分析将利用由 UCAR/Unidata 开发的 netCDF 软件。您可以在此处了解有关 Unidata 和网络公用数据格式 (NetCDF) 工程的详细信息。
Histogram bin-width optimization
- Shimazaki H. and Shinomoto S., A method for selecting the bin size of a time histogram in Neural Computation (2007) Vol. 19(6), 1503–1527.
- Terrell, G. and Scott, D., Oversmoothed Nonparametric Density Estimates. Journal of the American Statistical Association (1985) Vol. 80(389), 209-214.
- Online Statistics Education: A Multimedia Course of Study (http://onlinestatbook.com/). 项目主管:David M. Lane,莱斯大学(第 2 章,"Graphing Distributions, Histograms")。
Mann-Kendall trend test
- Hamed, K. H., Exact distribution of the Mann-Kendall trend test statistic for persistent data in Journal of Hydrology (2009), 86–94.
- Kendall, M. G., Gibbons, J. D., Rank correlation methods, fifth ed., (1990) Griffin, London.
- Mann, H. B., Nonparametric tests against trend in Econometrica (1945) Vol. 13, 245–259.