Durch Transformationen können Daten innerhalb eines Koordinatensystems verschoben werden. Sie werden häufig verwendet, um Daten von Digitalisierungsgeräten oder Scannern in Weltkoordinaten zu konvertieren. Sie können Transformationen auch verwenden, um die Maßeinheit der Daten innerhalb eines Koordinatensystems zu konvertieren, beispielsweise bei der Umwandlung von Fuß in Meter. Wenn Sie Daten zwischen Koordinatensystemen konvertieren möchten, wie z. B. geographische Daten in ein UTM-Koordinatensystem, projizieren Sie die Daten.
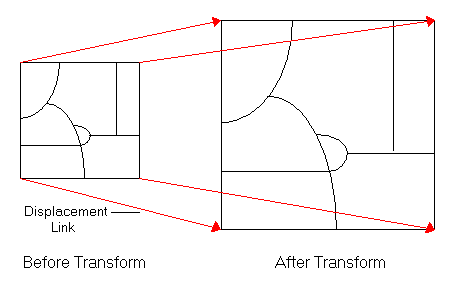
Die Transformationsfunktionen basieren auf dem Vergleich der Koordinaten der Quellen- und Zielpunkte, auch Passpunkte genannt, in speziellen grafischen Elementen, die als Versatz-Links bezeichnet werden. Bei Transformationen werden die Anfangs- und Zielpositionen (von und bis) der Links zur Erstellung der Transformationsformeln verwendet. Sie können diese Links interaktiv erstellen, indem Sie auf bekannte Quellen- und Zielpositionen zeigen, oder indem Sie eine Link-Textdatei oder eine Passpunktdatei laden.
Sie erstellen Links für Transformationen, um die sich entsprechenden Positionen in Quelle und Ziel miteinander zu verbinden. Beispiel: Sie möchten die Daten in einem Straßen-Layer transformieren oder verschieben, um sie an die Daten in einer Luftaufnahme anzupassen. Wenn Sie Versatz-Links erstellen, können Sie den Von-Punkt auf einem Schnittpunkt im Straßen-Layer und den Bis-Punkt auf dem entsprechenden Schnittpunkt in der Aufnahme platzieren. Die Anfangs- und Zielpunkte der Links müssen nicht auf Features platziert werden. Die Entfernung zwischen den Anfangs- und Zielpositionen kann in vielen Fällen sehr groß sein.
In ArcMap werden standardmäßig drei Transformationsmethoden unterstützt: affine, Ähnlichkeits- und projektive Transformation.
Affine Transformation
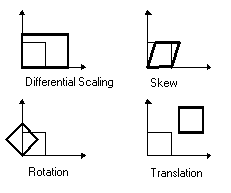
Bei einer affinen Transformation können die Daten unterschiedlich skaliert, verzerrt, gedreht und übertragen werden. In der folgenden Grafik sind die vier möglichen Änderungen dargestellt.
Die Funktion für die affine Transformation lautet
x’ = Ax + By + C
y’ = Dx + Ey + F wobei x und y Koordinaten des Eingabe-Layers und x' und y' die transformierten Koordinaten sind. A, B, C, D, E und F werden bestimmt, indem die Positionen der Quellen- und Zielpasspunkte miteinander verglichen werden. Sie skalieren, verzerren, rotieren und übertragen die Layer-Koordinaten. Für diese Methode sind mindestens drei Links erforderlich. Dies ist für die meisten Transformationen die empfohlene Einstellung.
Für die affine Transformation werden mindestens drei Versatz-Links benötigt.
Ähnlichkeitstransformation
Die Ähnlichkeitstransformation skaliert, dreht und überträgt die Daten. Die Achsen werden nicht unabhängig skaliert. Außerdem wird keine Verzerrung vorgenommen. Das Seitenverhältnis der transformierten Features wird beibehalten. Dies ist wichtig, wenn die relative Form der Features erhalten bleiben soll.
Die Funktion für die Ähnlichkeitstransformation lautet
x’ = Ax + By + Cy’ = -Bx + Ay + Fwobei
A = s * cos t
B = s * sin t
C = translation in x direction
F = translation in y direction und
s = scale change (same in x and y directions)
t = rotation angle, measured counterclockwise from the x-axisFür die Ähnlichkeitstransformation werden mindestens zwei Versatz-Links benötigt. Es sind jedoch drei oder mehr Links erforderlich, um ein quadratisches Mittel (root mean square, RMS) zu erzeugen.
Projektive Transformation
Die projektive Transformation basiert auf einer komplexeren Formel, für die mindestens vier Versatz-Links benötigt werden.
x’ = (Ax + By + C) / (Gx + Hy + 1)
y’ = (Dx + Ey + F) / (Gx + Hy + 1) Diese Methode wird angewendet, um Daten zu transformieren, die direkt bei Luftaufnahmen erfasst wurden. Weitere Informationen finden Sie in den photogrammetrischen Texten in den Hilfereferenzen für räumliche Anpassung.
Mathematischer Rest- und Durchschnittswert (RMS)
Die Transformationsparameter sind diejenigen Parameter, die am besten zwischen die Quellen- und Zielpasspunkte passen. Wenn Sie die Transformationsparameter verwenden, um die aktuellen Quellenpasspunkte zu transformieren, passen die transformierten Ausgabepositionen nicht zu den tatsächlichen Positionen der Ausgabepasspunkte. Dies wird als Residuenfehler bezeichnet; es handelt sich hierbei um eine Maßeinheit für die Übereinstimmung der tatsächlichen Positionen mit den transformierten Positionen der Ausgabepasspunkte. Dieser Fehler wird zu jedem Versatz-Link generiert.
Ein RMS-Fehler (Root Mean Square) wird zu jeder ausgeführten Transformation berechnet. Er gibt an, wie gut die abgeleitete Transformation ist. Im folgenden Beispiel ist die relative Position von vier Zielpasspunkten und die Position der transformierten Quellenpasspunkte dargestellt.
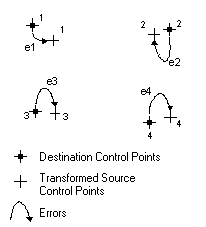
Der RMS-Fehler misst die Fehler zwischen den Zielpasspunkten und den transformierten Positionen der Quellenpasspunkte.
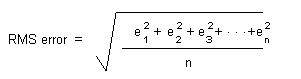
Die Transformation wird anhand der Methode der kleinsten Quadrate abgeleitet, sodass mehr Links als nötig erstellt werden können. Es müssen mindestens drei Links angegeben werden, um eine Transformation zu erzeugen, die zu einem RMS-Fehler führt.
Allgemein gilt: Je mehr Links Sie für eine Transformation platzieren, desto genauer ist das Ergebnis. Sie können die Genauigkeit der Transformation prüfen, indem Sie die RMS-Fehler in der Link-Tabelle anzeigen.
Transformationen ohne Zieldaten
In einigen Situationen müssen Sie eine Anpassung, in der Regel eine Transformation, ohne Daten an der Zielposition durchführen, d. h., Sie können den Bis-Punkt für Versatz-Links nicht interaktiv platzieren. Beispiel: Sie haben einige Daten digitalisiert und möchten eine Transformation von Digitalisierungseinheiten in reale Koordinaten durchführen. Wahrscheinlich kennen Sie die realen Koordinaten einiger Feature-Positionen in den Daten, z. B. einer Straßenkreuzung, des Standorts einer Quelle usw.
Sie können die Transformation einrichten, indem Sie Versatz-Links mit bekannten Positionen für die Anfangspositionen und temporären Punkten im Raum für die Zielpositionen erstellen. Anschließend können Sie den Zielkoordinaten der Links mithilfe der Link-Tabelle die entsprechenden realen Koordinaten zuweisen.