Zusammenfassung
Mit dem Werkzeug für die Regressionsanalyse werden alle möglichen Kombinationen von potenziellen erklärenden Variablen ausgewertet. Hierbei wird nach OLS-Modellen gesucht, die die abhängige Variable im Kontext von benutzerdefinierten Kriterien am besten erläutern.
Sie können die Ergebnisse dieses Werkzeugs (einschließlich der optionalen PDF-Berichtsdatei) über das Fenster Ergebnisse aufrufen. Wenn Sie die Hintergrundverarbeitung deaktivieren, werden die Ergebnisse auch in das Dialogfeld Fortschritt geschrieben.
Abbildung
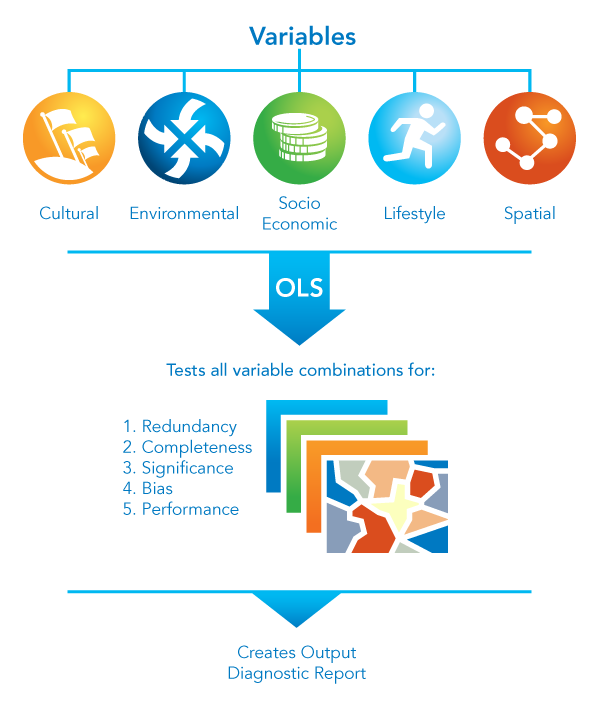
Verwendung
-
Die primäre Ausgabe für dieses Werkzeug ist eine Berichtsdatei, die im Fenster Ergebnisse ausgegeben wird. Klicken Sie im Fenster Ergebnisse mit der rechten Maustaste auf den Eintrag Meldungen und wählen Sie "Ansicht" aus, um den Zusammenfassungsbericht zur Regressionsanalyse in einem Meldungsdialogfeld anzuzeigen.
Mit diesem Werkzeug kann optional ein zusammenfassender Ergebnisbericht im Textformat erstellt werden. Diese Berichtsdatei wird dem Inhaltsverzeichnis hinzugefügt und kann in ArcMap angezeigt werden, indem Sie mit der rechten Maustaste darauf klicken und Öffnen wählen.
Mit diesem Werkzeug wird darüber hinaus optional eine Tabelle aller Modelle erstellt, die den Höchstwert für den p-Wert des Koeffizienten und das Wertekriterium Varianzinflationsfaktor (VIF) erfüllen. Eine vollständige Erklärung der Berichtselemente und -tabelle finden Sie unter Interpretieren der Regressionsanalyse-Ergebnisse.
Dieses Werkzeug verwendet Kleinste Quadrate (Ordinary Least Squares, OLS) und Räumliche Autokorrelation (Morans I). Die optionale Datei mit räumlicher Gewichtungsmatrix wird mit dem Werkzeug Räumliche Autokorrelation (Morans I) verwendet, um Modellresiduen zu bewerten. Sie wird nicht vom OLS-Werkzeug verwendet.
Dieses Werkzeug zieht alle Kombinationen der eingegebenen erklärenden Variablenkandidaten bei der Suche nach einem ordnungsgemäß angegebenen OLS-Modell heran. Nur in dem Fall, in dem das Werkzeug ein Modell findet, das den Schwellenwert für Minimaler annehmbarer Adj R-Squared, Maximaler p-Wert für Koeffizient - Grenzwert, Maximaler VIF-Wert - Grenzwert und Minimaler annehmbarer p-Wert Jarque Bera erfüllt, führt es das Werkzeug Räumliche Autokorrelation (Morans I) für die Modellresiduen aus, um zu ermitteln, ob die zu niedrigen/zu hohen Vorhersagen gruppiert sind. Um zumindest einige Informationen zur Residuengruppierung in dem Fall bereitstellen zu können, in dem keines der Modelle alle Kriterien erfüllt, wird der Test Räumliche Autokorrelation (Morans I) auch auf die Residuen der drei Modelle angewendet, die die höchsten Werte für "Adjusted R2" aufweisen sowie auf die drei Modelle, die die höchsten Jarque-Bera-p-Werte aufweisen.
Insbesondere dann, wenn die abhängige Variable eine starke räumliche Struktur aufweist, sollten Sie so viele potenzielle räumliche erklärende Variablen wie möglich zur Verfügung stellen. Einige Beispiele für räumliche Variablen sind die Entfernung zu Autobahnen, Zugänglichkeit von Arbeitsmöglichkeiten, Anzahl der örtlichen Einkaufsmöglichkeiten, Konnektivitätsmessungen oder Dichte. Wenn Sie keine erklärenden Variablen finden, die die räumliche Struktur der abhängigen Variablen erfassen, bestehen die Modellresiduen den Test in Bezug auf räumliche Autokorrelation höchstwahrscheinlich nicht. Eine deutliche Cluster-Bildung von Regressionsresiduen, wie durch das Werkzeug Räumliche Autokorrelation (Morans I) angegeben, weist auf falsche Modellangaben hin. Weitere Informationen über Strategien zum Handhaben von falschen Angaben finden Sie unter Was Sie noch nicht über die Regressionsanalyse wussten.
Da Räumliche Autokorrelation (Morans I) nicht für alle getesteten Modelle ausgeführt wird (siehe vorherigen Nutzungstipp), fehlen in der Ausgabeergebnistabelle Daten für das Feld SA (Räumliche Autokorrelation). Da in DBF (.dbf)-Dateien keine NULL-Werte gespeichert werden können, werden diese als sehr kleine (negative) Zahlen angezeigt (beispielsweise -1.797693e+308). In Geodatabase-Tabellen werden diese fehlenden Werte als NULL-Werte angezeigt. Ein fehlender Wert weist darauf hin, dass die Residuen für das zugehörige Modell nicht auf räumliche Autokorrelation getestet wurden, da das Modell nicht alle anderen Modell-Suchkriterien erfüllt hat.
Die standardmäßige Datei mit räumlicher Gewichtungsmatrix, die die zum Ausführen des Werkzeugs Räumliche Autokorrelation (Morans I) verwendet wird, basiert auf einer 8-Nächste-Nachbarn-Konzeptionalisierung von räumlichen Beziehungen. Diese Standardeinstellung wurde primär deshalb gewählt, da sie schnell ausgeführt wird. Um die Nachbarbeziehungen anders zu definieren, können Sie einfach eine eigene räumliche Gewichtungsmatrixdatei mit dem Werkzeug Räumliche Gewichtungsmatrix erstellen erstellen und dann den Namen dieser Datei für den Parameter Eingegebene räumliche Gewichtungsmatrix-Datei angeben. "Inverse Entfernung", "Polygonnachbarschaft" oder "Nächste Nachbarn (K)" sind alles geeignete Konzeptualisierungen von räumlichen Beziehungen zum Testen von Regressionsresiduen.
Syntax
ExploratoryRegression(Input_Features, Dependent_Variable, Candidate_Explanatory_Variables, {Weights_Matrix_File}, {Output_Report_File}, {Output_Results_Table}, {Maximum_Number_of_Explanatory_Variables}, {Minimum_Number_of_Explanatory_Variables}, {Minimum_Acceptable_Adj_R_Squared}, {Maximum_Coefficient_p_value_Cutoff}, {Maximum_VIF_Value_Cutoff}, {Minimum_Acceptable_Jarque_Bera_p_value}, {Minimum_Acceptable_Spatial_Autocorrelation_p_value})| Parameter | Erklärung | Datentyp |
Input_Features | Die Feature-Class oder der Feature-Layer, die bzw. der die abhängigen und erklärenden Variablenkandidaten für die Analyse enthält. | Feature Layer |
Dependent_Variable | Das numerische Feld mit den beobachteten Werten, die Sie mit OLS modellieren möchten. | Field |
Candidate_Explanatory_Variables [Candidate_Explanatory_Variables,...] | Eine Liste mit Feldern, die als erklärende Variablen für das OLS-Modell herangezogen werden können. | Field |
Weights_Matrix_File (optional) | Eine Datei, die räumliche Gewichtungen enthält, mit denen die räumlichen Beziehungen zwischen den Eingabe-Features definiert werden. Diese Datei wird für die Bewertung der räumlichen Autokorrelation zwischen Regressionsresiduen verwendet. Mit dem Werkzeug Räumliche Gewichtungsmatrix erstellen können Sie die Datei erstellen. Wenn Sie keine räumliche Gewichtungsmatrixdatei bereitstellen, werden Residuen für die räumliche Autokorrelation basierend auf den 8 nächsten Nachbarn der einzelnen Features ausgewertet. Hinweis: Die räumliche Gewichtungsmatrixdatei wird nur für die Analyse der räumlichen Struktur in Modellresiduen verwendet. Sie wird nicht zum Erstellen oder Kalibrieren der OLS-Modelle herangezogen. | File |
Output_Report_File (optional) | Die Berichtsdatei enthält die Ergebnisse der Werkzeugoperationen, einschließlich Details zu Modellen, die alle von Ihnen eingegebenen Suchkriterien erfüllen. Diese Ausgabedatei enthält auch Diagnosen, mit denen Sie häufige Regressionsprobleme beheben können, falls keine bestandenen Modelle gefunden wurden. | File |
Output_Results_Table (optional) | Die optional erstellte Ausgabetabelle mit den erklärenden Variablen und Diagnosen für alle Modelle innerhalb der Grenzwerte für den p-Wert des Koeffizienten und den VIF-Wert. | Table |
Maximum_Number_of_Explanatory_Variables (optional) | Es werden alle Modelle mit erklärenden Variablen bis zu dem hier eingegebenen Wert ausgewertet. Wenn zum Beispiel Minimum_Number_of_Explanatory_Variables den Wert 2 und Maximum_Number_of_Explanatory_Variables den Wert 3 aufweist, zieht das Werkzeug Regressionsanalyse alle Modelle mit allen möglichen Kombinationen der beiden erklärenden Variablen sowie alle Modelle mit allen möglichen Kombinationen der drei erklärenden Variablen heran. | Long |
Minimum_Number_of_Explanatory_Variables (optional) | Dieser Wert stellt die minimale Anzahl erklärender Variablen für die auszuwertenden Modelle dar. Wenn zum Beispiel Minimum_Number_of_Explanatory_Variables den Wert 2 und Maximum_Number_of_Explanatory_Variables den Wert 3 aufweist, zieht das Werkzeug Regressionsanalyse alle Modelle mit allen möglichen Kombinationen der beiden erklärenden Variablen sowie alle Modelle mit allen möglichen Kombinationen der drei erklärenden Variablen heran. | Long |
Minimum_Acceptable_Adj_R_Squared (optional) | Dies ist der niedrigste Wert für "Adjusted R-Squared", der für ein bestandenes Modell vorausgesetzt wird. Wenn ein Modell allen Suchkriterien entspricht, jedoch einen niedrigeren Wert als den hier für "Adjusted R-Squared" eingegebenen Wert aufweist, wird es in der Output_Report_FileAusgabeberichtsdatei nicht als bestandenes Modell aufgeführt. Gültige Werte für diesen Parameter liegen zwischen 0,0 und 1,0. Der Standardwert ist 0,5 und gibt an, dass bestandene Modelle mindestens fünfzig Prozent der Variation in der abhängigen Variablen erklären. | Double |
Maximum_Coefficient_p_value_Cutoff (optional) | Für jedes ausgewertete Modell berechnet OLS Koeffizienten-p-Werte der erklärenden Variable. Der hier eingegebene Grenzwert für den p-Wert stellt das Konfidenzniveau dar, das für alle Koeffizienten im Modell erforderlich ist, um das Modell als bestanden anzusehen. Kleinere p-Werte stellen ein höheres Konfidenzniveau dar. Gültige Werte für diesen Parameter liegen zwischen 1,0 und 0,0. In den meisten Fällen sind es Werte wie 0,1, 0,05, 0,01, 0,001 usw. Der Standardwert ist 0,05 und gibt an, dass bestandene Modelle nur solche erklärenden Variablen enthalten, deren Koeffizienten ein statistisches Konfidenzniveau von 95 Prozent aufweisen (p-Werte kleiner als 0,05). Um diesen Standardwert auszuweiten, geben Sie einen höheren Grenzwert für den p-Wert an, zum Beispiel 0,1. Wenn sich sehr viele bestandene Modelle ergeben, sollten Sie dieses Suchkriterium einschränken, indem Sie den standardmäßigen Grenzwert für den p-Wert von 0,05 auf 0,01 oder weniger verringern. | Double |
Maximum_VIF_Value_Cutoff (optional) | Dieser Wert gibt an, wie viel Redundanz (Multikollinearität) Sie zwischen den erklärenden Variablen des Modells tolerieren. Wenn der Wert für den Varianzinflationsfaktor (Variance Inflation Factor, VIF) höher ist als ca. 7,5, kann die Multikollinearität dazu führen, dass das Modell instabil wird; daher ist 7,5 in diesem Fall der Standardwert. Wenn die bestandenen Modelle weniger Redundanz aufweisen sollen, geben Sie einen niedrigeren Wert für diesen Parameter ein, beispielsweise 5,0. | Double |
Minimum_Acceptable_Jarque_Bera_p_value (optional) | Der vom Jarque-Bera-Diagnosetest zurückgegebene p-Wert gibt an, ob die Modellresiduen normal verteilt sind. Wenn der p-Wert statistisch signifikant (klein) ist, sind die Modellresiduen nicht normal, d. h. das Modell ist verzerrt. Bestandene Modelle müssen einen hohen Jarque-Bera-p-Wert aufweisen. Der zulässige Standard-Mindestwert für den p-Wert ist 0,1. Als bestanden werden nur solche Modelle betrachtet, die höhere p-Werte als diesen Mindestwert zurückgeben. Wenn keine unverzerrten bestandenen Modelle gefunden werden und Sie dieses Kriterium ausweiten möchten, können Sie einen niedrigeren Mindestwert für den p-Wert eingeben, beispielsweise 0,05. | Double |
Minimum_Acceptable_Spatial_Autocorrelation_p_value (optional) | Bei Modellen, die alle anderen Suchkriterien erfüllen, werden mit dem Werkzeug Regressionsanalyse die Modellresiduen auf räumliche Cluster-Bildung mit Morans I überprüft. Wenn der p-Wert dieses Diagnosetests statistisch signifikant (klein) ist, weist dies darauf hin, dass im Modell höchstwahrscheinlich wichtige erklärende Variablen fehlen. Wenn die Regressionsresiduen eine räumliche Autokorrelation aufweisen, ist das Modell falsch angegebenen, und die Ergebnisse sind somit nicht vertrauenswürdig. Bestandene Modelle müssen hohe p-Werte für diesen Diagnosetest aufweisen. Der Standard-Mindestwert für den p-Wert ist 0,1. Als bestanden werden nur solche Modelle betrachtet, die höhere p-Werte als diesen Mindestwert zurückgeben. Wenn aufgrund dieses Diagnosetests keine ordnungsgemäß angegebenen Modelle gefunden werden können und Sie dieses Suchkriterium erweitern möchten, können Sie einen niedrigeren Mindestwert eingeben, beispielsweise 0,05. | Double |
Codebeispiel
ExploratoryRegression – Beispiel 1 (Python-Fenster)
Das folgende Skript im Python-Fenster veranschaulicht, wie Sie das Werkzeug "ExploratoryRegression" verwenden.
import arcpy
import os
arcpy.env.workspace = r"C:\ER"
arcpy.ExploratoryRegression_stats("911CallsER.shp",
"Calls",
"Pop;Jobs;LowEduc;Dst2UrbCen;Renters;Unemployed;Businesses;NotInLF; \
ForgnBorn;AlcoholX;PopDensity;MedIncome;CollGrads;PerCollGrd; \
PopFY;JobsFY;LowEducFY",
"BG_911Calls.swm", "BG_911Calls.txt", "",
"MAX_NUMBER_ONLY", "5", "1", "0.5", "0.05", "7.5", "0.1", "0.1")
ExploratoryRegression – Beispiel 2 (eigenständiges Python-Skript)
Das folgende eigenständige Python-Skript veranschaulicht, wie Sie das Werkzeug "ExploratoryRegression" verwenden.
# Exploratory Regression of 911 calls in a metropolitan area
# using the Exploratory Regression Tool
# Import system modules
import arcpy
import os
# Set property to overwrite existing output, by default
arcpy.env.overwriteOutput = True
try:
# Set the current workspace (to avoid having to specify the full path to
# the feature classes each time)
arcpy.env.workspace = r"C:\ER"
# Join the 911 Call Point feature class to the Block Group Polygon feature class
# Process: Spatial Join
fieldMappings = arcpy.FieldMappings()
fieldMappings.addTable("BlockGroups.shp")
fieldMappings.addTable("911Calls.shp")
sj = arcpy.SpatialJoin_analysis("BlockGroups.shp", "911Calls.shp", "BG_911Calls.shp",
"JOIN_ONE_TO_ONE",
"KEEP_ALL",
fieldMappings,
"COMPLETELY_CONTAINS", "", "")
# Delete extra fieldsto clean up the data
# Process: Delete Field
arcpy.DeleteField_management("BG_911Calls.shp", "OBJECTID;INC_NO;DATE_;MONTH_;STIME; \
SD_T;DISP_REC;NFPA_TYP;CALL_TYPE;RESP_COD;NFPA_SF; \
SIT_FND;FMZ_Q;FMZ;RD;JURIS;COMPANY;COMP_COD;RESP_YN; \
DISP_DT;DAY_;D1_N2;RESP_DT;ARR_DT;TURNOUT;TRAVEL; \
RESP_INT;ADDRESS_ID;CITY;CO;AV_STATUS;AV_SCORE; \
AV_SIDE;Season;DayNight")
# Create Spatial Weights Matrix for Calculations
# Process: Generate Spatial Weights Matrix
swm = arcpy.GenerateSpatialWeightsMatrix_stats("BG_911Calls.shp", "TARGET_FID", "BG_911Calls.swm",
"CONTIGUITY_EDGES_CORNERS",
"EUCLIDEAN", "1", "", "", "ROW_STANDARDIZATION", "", "", "", "")
# Exploratory Regression Analysis for 911 Calls
# Process: Exploratory Regression
er = arcpy.ExploratoryRegression_stats("BG_911Calls.shp",
"Calls",
"Pop;Jobs;LowEduc;Dst2UrbCen;Renters;Unemployed;Businesses;NotInLF; \
ForgnBorn;AlcoholX;PopDensity;MedIncome;CollGrads;PerCollGrd; \
PopFY;JobsFY;LowEducFY",
"BG_911Calls.swm", "BG_911Calls.txt", "",
"MAX_NUMBER_ONLY", "5", "1", "0.5", "0.05", "7.5", "0.1", "0.1")
except:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())
Umgebungen
Lizenzinformationen
- Basic: Ja
- Standard: Ja
- Advanced: Ja
Verwandte Themen
- Überblick über das Toolset "Modellierung von räumlichen Beziehungen"
- Funktionsweise der Regressionsanalyse
- Grundlagen zur Regressionsanalyse
- Was Sie noch nicht über die Regressionsanalyse wussten
- Interpretieren der Ergebnisse des Werkzeugs "Regressionsanalyse"
- Interpretieren von OLS-Ergebnissen
- Geographisch gewichtete Regression (GWR)
- Räumliche Autokorrelation (Morans I)
- Was ist ein Z-Wert? Was ist ein p-Wert?
- Funktionsweise der OLS-Regression