Die Toolbox "Spatial Statistics" enthält effektive Werkzeuge zum Auswerten räumlicher Muster. Mit dem Werkzeug Hot-Spot-Analyse etwa können Sie Fragen wie die folgenden stellen:
- Gibt es Orte in den USA, an denen Personen immer sehr jung sterben?
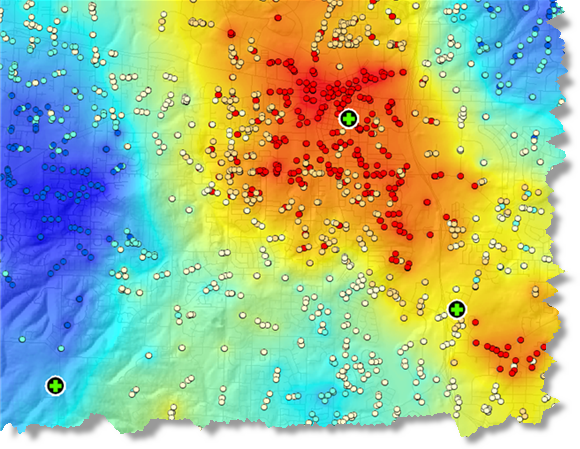
- Wo sind die Hot-Spots von Verbrechen, Notrufen (siehe Abbildung unten) oder Bränden?
- Wo ist der Anteil der Verkehrsunfälle in einer Stadt höher als erwartet?
Bei jedem dieser Punkte wird nach dem "wo" gefragt. Die nächste logische Frage für die obengenannten Analysetypen lautet "warum?"
- Warum gibt es Orte in den USA, an denen Personen immer sehr jung sterben? Welche Ursache kann dies haben?
- Können wir die Eigenschaften von Orten modellieren, an denen es viele Verbrechen, Notrufe oder Brände gibt, um zur Reduzierung dieser Vorfälle beizutragen?
- Welche Faktoren tragen zu einer höheren Verkehrsunfallquote als erwartet bei? Gibt es Regelungen oder abschwächende Maßnahmen, mit denen die Zahl der Verkehrsunfälle in der Stadt und/oder insbesondere in Gebieten mit hoher Unfallrate reduziert werden kann?
Die Werkzeuge im Toolset "Modellierung von räumlichen Beziehungen" unterstützen Sie bei der Beantwortung dieses zweiten Fragetyps. Zu diesen Werkzeugen zählen die Regression Kleinste Quadrate (Ordinary Least Squares) (OLS) und die geographisch gewichtete Regression.
Räumliche Beziehungen
Mit Regressionsanalysen können Sie räumliche Beziehungen modellieren, überprüfen und erkunden und die Faktoren hinter beobachteten räumlichen Mustern erklären. Beispielsweise können Sie sich fragen, warum Personen in bestimmten Regionen des Landes immer sehr jung sterben oder welche Faktoren zu einer unerwartet hohen Diabetesrate beitragen. Durch die Modellierung räumlicher Beziehungen kann die Regressionsanalyse jedoch auch für Prognosen eingesetzt werden. Die Modellierung der Faktoren, die zu Universitätsabschlussraten beitragen, ermöglicht beispielsweise die Vorhersage von zukünftigen Qualifikationen und Ressourcen auf dem Arbeitsmarkt. Außerdem können Sie mittels Regression Regenfälle oder die Luftqualität vorhersagen, wenn die Interpolation aufgrund von nur wenigen Überwachungsstationen nicht ausreichend ist (an Berghängen und in Tälern gibt es beispielsweise oft keine Niederschlagsmesser).
OLS ist die bekannteste Regressionstechnik. Dies ist auch der richtige Ausgangspunkt für alle räumlichen Regressionsanalysen. OLS bietet ein globales Modell der Variablen oder des Prozesses, die bzw. den Sie zu verstehen oder vorherzusagen versuchen (früher Tod/Regenfälle); es erstellt eine einzelne Regressionsgleichung zur Darstellung dieses Prozesses. Die geographisch gewichtete Regression (GWR) ist eine von mehreren räumlichen Regressionstechniken, die zunehmend in der Geographie und anderen Disziplinen eingesetzt wird. GWR bietet ein lokales Modell der Variablen oder des Prozesses, die bzw. den Sie zu verstehen oder vorherzusagen versuchen, indem eine Regressionsgleichung an jedes Feature im Dataset angepasst wird. Wenn sie richtig verwendet werden, ermöglichen diese Methoden aussagekräftige und zuverlässige Statistiken zur Untersuchung und Schätzung linearer Beziehungen.
Lineare Beziehungen sind entweder positiv oder negativ. Wenn Sie feststellen, dass die Anzahl der Such- und Rettungsaktionen mit zunehmender Tagestemperatur zunimmt, wird von einer positiven Beziehung gesprochen; es gibt eine positive Korrelation. Bei dieser positiven Beziehung kann auch davon gesprochen werden, dass die Such- und Rettungsaktionen mit sinkenden Tagestemperaturen abnehmen. Wenn Sie dagegen feststellen, dass die Anzahl der Verbrechen in dem Maße sinkt, in dem die Anzahl der patroullierenden Polizisten in einem Gebiet zunimmt, ist die Beziehung negativ. Sie können diese negative Beziehung auch dadurch ausdrücken, dass Sie angeben, die Anzahl der Verbrechen nimmt in dem Maße zu, in dem die Anzahl der patroullierenden Polizisten abnimmt. In der folgenden Abbildung werden sowohl positive als auch negative Beziehungen und der Fall, in dem es keine Beziehung zwischen zwei Variablen gibt, dargestellt:
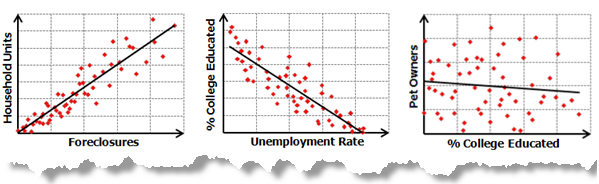
Bei Korrelationsanalysen und den ihnen zugeordneten Grafiken (Abbildung oben) wird die Stärke der Beziehung zwischen zwei Variablen getestet. Regressionsanalysen dagegen gehen einen Schritt weiter: Es wird versucht zu zeigen, in welchem Grad eine oder mehrere Variablen potenziell positive oder negative Änderungen bei einer anderen Variable hervorrufen.
Regressionsanalyseanwendungen
Die Regressionsanalyse kann für eine große Zahl von Anwendungen verwendet werden:
- Modellierung von Sekundarschulbesuchsraten, um die Faktoren ermitteln zu können, die Kinder davon abhalten, die Schule zu verlassen.
- Modellieren von Verkehrsunfällen als Funktion von Geschwindigkeit, Straßenbedingungen, Wetter usw., um Richtlinien zur Reduzierung der Unfälle zu entwerfen.
- Modellieren von Immobilienverlust infolge eines Brandes als Funktion von Variablen wie Grad der Feuerwehrbeteiligung, Reaktionszeit oder Immobilienwert. Wenn Sie feststellen, dass die Reaktionszeit ein wichtiger Faktor ist, müssen möglicherweise mehr Feuerwachen gebaut werden. Stellt sich dagegen heraus, dass die Stärke der Feuerwehr ein wichtiger Faktor ist, müssen Sie die Anzahl der Ausrüstungsgegenstände und der entsendeten Feuerwehrmänner erhöhen.
Es gibt vor allem drei Gründe, aus denen sich die Verwendung der Regressionsanalyse empfiehlt:
- Modellieren eines Phänomens, um es besser zu verstehen und entsprechende Richtlinien entwickeln oder Entscheidungen zu geeigneten Maßnahmen treffen zu können. Das Hauptziel besteht darin zu messen, in welchem Maß Änderungen bei einer oder mehreren Variablen gemeinsam Änderungen bei einer anderen Variablen bewirken. Beispiel: Verstehen der wichtigsten Eigenschaften des Lebensraums einer besonders gefährdeten Vogelart (z. B. Niederschlag, Nahrungsquellen, Vegetation, Raubtiere), um Gesetze zum Schutz dieser Spezies entwerfen zu können.
- Modellieren eines Phänomens, um Werte an anderen Orten oder zu anderen Zeiten vorhersagen zu können. Das Hauptziel besteht in der Erstellung eines Vorhersagemodells, das sowohl konsistent als auch genau ist. Beispiel: Mit welcher Nachfrage für Elektrizität ist unter Berücksichtigung der Prognosen zum Bevölkerungswachstum und den durchschnittlichen Wetterbedingungen im nächsten Jahr zu rechnen?
- Sie können die Regressionsanalyse auch anwenden, um Hypothesen zu durchleuchten. Angenommen, Sie modellieren die Verbrechen in einem Wohngebiet, um sie besser verstehen und nach Möglichkeit Regelungen einführen zu können, die diese verhindern. Zu Beginn der Analyse haben Sie wahrscheinlich Fragen oder Hypothesen, die Sie untersuchen möchten:
- Die Broken-Windows-Theorie besagt, dass die Entwertung öffentlichen Eigentums (Graffiti, Strukturbeschädigungen usw.) andere Verbrechen nach sich zieht. Besteht eine positive Beziehung zwischen Vandalismusvorfällen und Wohnungseinbrüchen?
- Besteht eine Beziehung zwischen illegalem Drogenkonsum und Einbrüchen (stehlen Drogenabhängige, um ihre Gewohnheiten aufrechtzuerhalten)?
- Suchen Einbrecher ihre Opfer gezielt aus? Gibt es möglicherweise mehr Vorfälle in Wohngebieten mit einem höheren Prozentsatz an älteren oder weiblichen Haushalten?
- Ist das Einbruchsrisiko für Personen höher, wenn sie in einer wohlhabenden oder armen Gegend leben?
Begriffe und Konzepte im Zusammenhang mit der Regressionsanalyse
Um die Regressionsanalyse erläutern zu können, müssen Sie zuerst mit einigen Begriffen und grundlegenden Konzepten der Regressionsstatistik vertraut werden:
Regressionsgleichung: Dies ist die mathematische Formel, die auf die erklärenden Variablen angewendet wird, um die abhängige Variable, die modelliert werden soll, bestmöglich vorhersagen zu können. Unglücklicherweise für Geowissenschaftler, die X und Y als Koordinaten betrachten, lautet die Notation in Regressionsgleichungen für die abhängige Variable immer Y und für die unabhängigen oder erklärenden Variablen immer X. Jede unabhängige Variable wird einem Regressionskoeffizienten zugeordnet, der die Aussagekraft und das Vorzeichen der Variablenbeziehung zur abhängigen Variable beschreibt. Eine Regressionsgleichung kann folgendermaßen aussehen (Y ist die abhängige Variable, X sind die erklärenden Variablen und β sind die Regressionskoeffizienten; jede dieser Komponenten der Regressionsgleichung wird im Folgenden erläutert):
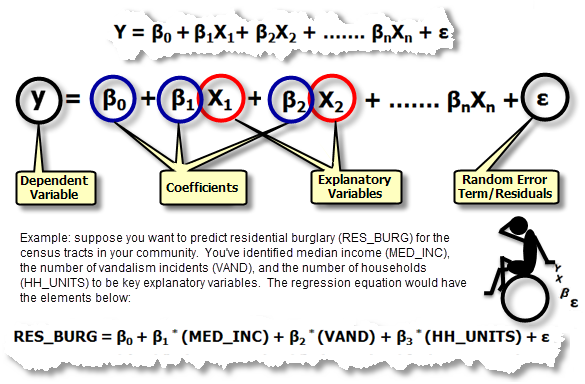
- Abhängige Variable (Y): Diese Variable stellt den Prozess dar, den Sie vorhersagen oder verstehen möchten (Wohnungseinbrüche, Zwangsvollstreckung, Regenfälle). In der Regressionsgleichung steht sie auf der linken Seite des Gleichheitszeichens. Mit der Regression können Sie die abhängige Variable vorhersagen, Sie starten jedoch immer mit einer Reihe bekannter Y-Werte und erstellen (oder kalibrieren) mit diesen das Regressionsmodell. Die bekannten Y-Werte werden oft als beobachtete Werte bezeichnet.
- Unabhängige/erklärende Variablen (X): Mit diesen Variablen werden die abhängigen Variablenwerte modelliert oder vorhergesagt. In der Regressionsgleichung werden sie auf der rechten Seite des Gleichheitszeichens angezeigt und oft als erklärende Variablen bezeichnet. Die abhängige Variable ist eine Funktion der erklärenden Variablen. Wenn Sie die jährlichen Käufe eines potenziellen Geschäfts vorhersagen möchten, können Sie erklärende Variablen hinzufügen, die z. B. die Anzahl der potenziellen Kunden, Entfernung zu Wettbewerbern, Geschäftstransparenz und lokale Konsummuster darstellen.
- Regressionskoeffizienten (β): Koeffizienten werden vom Regressionswerkzeug berechnet. Hierbei handelt es sich um Werte (einen pro erklärender Variable), die die Stärke und den Typ der Beziehung zwischen der erklärenden Variable und der abhängigen Variable angeben. Angenommen, Sie modellieren die Brandhäufigkeit als Funktion von Sonneneinstrahlung, Vegetation, Niederschlag und Ausrichtung. Es steht eine positive Beziehung zwischen der Brandhäufigkeit und Sonneinstrahlung zu erwarten (in anderen Worten, je mehr Sonne, desto häufiger treten Brände auf). Wenn die Beziehung positiv ist, ist auch das Vorzeichen des zugeordneten Koeffizienten positiv. Zwischen der Brandhäufigkeit und Niederschlägen würde eine negative Beziehung erwartet (in anderen Worten, je mehr Regen, desto weniger Brände). Koeffizienten für negative Beziehungen haben negative Vorzeichen. Wenn es sich um eine starke Beziehung handelt, ist der Koeffizient relativ groß (relativ zu den Einheiten der erklärenden Variable, mit denen er verknüpft ist). Schwache Beziehungen sind Koeffizienten nahe Null zugeordnet; β0 ist der Schnittpunkt der Regression. der Regression. Er stellt den erwarteten Wert für die abhängige Variable dar, wenn alle unabhängigen (erklärenden) Variablen Null sind.
P-Werte: Bei den meisten Regressionsmethoden wird ein statistischer Test durchgeführt, um eine Wahrscheinlichkeit (einen sogenannten P-Wert) für die den einzelnen unabhängigen Variablen zugeordneten Koeffizienten zu berechnen. Die Null-Hypothese für diesen statistischen Test gibt an, dass sich ein Koeffizient nicht deutlich von Null abhebt (in anderen Worten, der Koeffizient ist für alle Zwecke gleich Null und die erklärende Variable bringt das Modell nicht voran). Kleine P-Werte geben geringe Wahrscheinlichkeiten wieder und deuten darauf hin, dass der Koeffizient tatsächlich mit einem Wert, der sich deutlich von Null unterscheidet, bedeutend für das Modell ist (in anderen Worten, ein kleiner P-Wert bedeutet, dass der Koeffizient nicht Null ist). Beispielsweise wird bei einem Koeffizienten mit dem P-Wert 0,01 angenommen, dass der P-Wert im Konfidenzniveau von 99 Prozent statistisch signifikant ist; die zugeordnete Variable ermöglicht eine effektive Vorhersage. Variablen mit Koeffizienten nahe Null sind bei der Prognose oder Modellierung der abhängigen Variable nicht hilfreich; sie werden nahezu immer aus der Regressionsgleichung entfernt, sofern keine wichtigen theoretischen Gründe dafür sprechen, sie beizubehalten.
R 2/R-Squared: Multiple R-Squared- und Adjusted R-Squared-Werte sind Statistiken, die zum Auswerten der Modell-Performance aus der Regressionsgleichung abgeleitet werden. Der R-Squared-Wert reicht von 0 bis 100 Prozent. Wenn das Modell perfekt mit den beobachteten Werten der abhängigen Variable übereinstimmt, ist R-Squared 1,0 (und Sie haben zweifellos einen Fehler gemacht, etwa eine Form von Y zur Vorhersage von Y verwendet). Wahrscheinlicher etwa sind R-Squared-Werte wie 0,49, die folgendermaßen interpretiert werden können: "Dieses Modell erklärt 49 Prozent der Variation in der abhängigen Variable". Um zu verstehen, worauf der R-Squared-Wert abzielt, erstellen Sie ein Balkendiagramm, in dem die geschätzten und beobachteten Y-Werte nach geschätzten Werten sortiert dargestellt werden. Beachten Sie, wie viel Überlappung es gibt. Diese Abbildung bietet eine visuelle Darstellung dessen, wie gut die vorhergesagten Werte des Modells die Variation in den beobachteten abhängigen Variablenwerten erklären. Abbildung anzeigen. Der Adjusted R-Squared-Wert ist immer etwas niedriger als der Multiple R-Squared-Wert, da er die Modellkomplexität (die Anzahl von Variablen) im Verhältnis zu den Daten widerspiegelt. Daher ist der Adjusted R-Squared-Wert ein etwas genaueres Maß für die Modell-Performance.
Residuen: Hierbei handelt es sich um den nicht erklärten Teil der abhängigen Variable, der in der Regressionsgleichung vom Zufallsfehlerterm ε dargestellt wird. Abbildung anzeigen. Bekannte Werte für die abhängige Variable werden verwendet, um das Regressionsmodell zu erstellen und zu kalibrieren. Mithilfe der bekannten Werte für die abhängige Variable (Y) und der bekannten Werte für alle erklärenden Variablen (X-Werte) erstellt das Regressionswerkzeug eine Gleichung, mit der diese bekannten Y-Werte so genau wie möglich vorhergesagt werden. Die vorhergesagten Werte stimmen jedoch äußerst selten genau mit den beobachteten Werten überein. Der Unterschied zwischen den beobachteten Y-Werten und den vorhergesagten Y-Werten wird als Residuen bezeichnet. Der Betrag der Residuen einer Regressionsgleichung ist ein Maß für die Modellanpassung. Große Residuen weisen auf eine schlechte Modellanpassung hin.
Die Erstellung eines Regressionsmodells ist ein iterativer Prozess, bei dem effektive unabhängige Variablen gesucht werden, um die abhängige Variable zu erklären, die Sie modellieren oder verstehen möchten, und dann das Regressionsmodell auszuführen und damit zu bestimmen, welche Variablen effektive Prognosen ermöglichen. Danach werden Variablen wiederholt entfernt und/oder hinzugefügt, bis Sie das bestmögliche Regressionsmodell gefunden haben. Der Modellerstellungsprozess muss oft erst gesucht werden, es sollte sich dabei jedoch nie um eine "Angelexpedition" handeln. Ermitteln Sie mögliche erklärende Variablen mithilfe der Theorie, Experten vor Ort und Ihrem gesunden Menschenverstand. Sie sollten die erwartete Beziehung zwischen jeder potenziellen erklärenden Variable und der abhängigen Variable vor der Analyse angeben und begründen können und Modelle infrage stellen, bei denen diese Beziehungen nicht übereinstimmen.
Probleme bei der Regressionsanalyse
Die OLS-Regression ist eine einfache Methode mit einer weit entwickelten Theorie und einer Reihe von effektiven Diagnosemöglichkeiten, die bei der Interpretation und Problembehandlung hilfreich sind. OLS ist jedoch nur dann effektiv und zuverlässig, wenn die Daten und das Regressionsmodell allen Annahmen entsprechen, die für diese Methode erforderlich sind (siehe Tabelle unten). Räumliche Daten verstoßen oft gegen die Annahmen und Anforderungen der OLS-Regression, deshalb ist es wichtig, Regressionsmodelle zusammen mit geeigneten Diagnosewerkzeugen zu verwenden, mit denen bewertet werden kann, ob die Regression in Anbetracht der Datenstruktur und des implementierten Modells eine geeignete Methode für Ihre Analyse darstellt.
Wie Regressionsmodelle ungültig werden
Ein schwerwiegender Verstoß stellen bei vielen Regressionsmodellen ungenügende Angaben dar. Ein Modell mit ungenügenden Angaben ist nicht vollständig. Es fehlen wichtige erklärende Variablen, deshalb wird nicht adäquat dargestellt, was Sie zu modellieren oder vorherzusagen versuchen (die abhängige Variable Y). In anderen Worten, das Regressionsmodell erfasst nur einen Teilbereich. Ungenügende Angaben werden festgestellt, wenn eine statistisch signifikante räumliche Autokorrelation in den Regressionsresiduen vorkommt oder – anders ausgedrückt – wenn Sie bemerken, dass die zu hohen und zu niedrigen Vorhersagen (Residuen) aus dem Modell zur räumlichen Cluster-Bildung tendieren, sodass der Cluster mit zu hohen Vorhersagen in einigen Teilen des Untersuchungsgebiets liegt und der Cluster mit zu niedrigen Vorhersagen in anderen. Die Zuordnung von Regressionsresiduen oder die mit der Analyse der geographisch gewichteten Regression verknüpften Koeffizienten bietet oft Anhaltspunkte für fehlende Angaben. Die Ausführung der Hot-Spot-Analyse für Regressionsresiduen kann ebenfalls dazu beitragen, verschiedene räumliche Ordnungen zu enthüllen, die in OLS mit regionalen Variablen modelliert oder mithilfe der geographisch gewichteten Regressionsmethode behoben werden können. Angenommen, Sie ordnen Ihre Regressionsresiduen zu und bemerken, dass bei dem Modell stets zu hohe Vorhersagen in Gebirgsregionen und zu niedrige Vorhersagen in Tälern getroffen werden. Daraus können Sie schließen, dass eine Höhenvariable im Modell fehlt. Es gibt jedoch auch Situationen, in denen die fehlenden Variablen zu komplex für die Modellierung sind, unmöglich ausgewertet werden können oder zu schwierig zu messen sind. In diesen Fällen können Sie möglicherweise zu GWR oder einer anderen räumlichen Regressionsmethode wechseln, um ein aussagekräftiges Modell zu erhalten.
In der folgenden Tabelle werden allgemeine Probleme bei Regressionsmodellen mit den Werkzeugen aufgeführt, die in ArcGIS verfügbar sind, um sie zu lösen:
Allgemeine Regressionsprobleme, Folgen und Lösungen
Fehlende erklärende Variablen (ungenügende Angaben). | Wenn wichtige erklärende Variablen in einem Regressionsmodell fehlen, sind die Koeffizienten und die ihnen zugeordneten P-Werte nicht zuverlässig. | Ordnen Sie OLS-Residuen und GWR-Koeffizienten zu und untersuchen Sie sie, oder führen Sie die Hot-Spot-Analyse für OLS-Regressionsresiduen aus, um festzustellen, ob Sie so Rückschlüsse auf mögliche fehlende Variablen ziehen können. |
Nicht lineare Beziehungen. Abbildung anzeigen. | OLS und GWR sind beides lineare Methoden. Wenn die Beziehung zwischen einer der erklärenden Variablen und der abhängigen Variable nicht linear ist, hat das resultierende Modell eine schlechte Performance. | Erstellen Sie ein Scatterplotmatrix-Diagramm, um die Beziehungen zwischen allen Variablen im Modell aufzuklären. Achten Sie sorgfältig auf Beziehungen in Zusammenhang mit der abhängigen Variable. Krummlinigkeit kann oft durch die Transformation der Variablen beseitigt werden. Abbildung anzeigen. Verwenden Sie alternativ eine nicht lineare Regressionsmethode. |
Datenausreißer. Abbildung anzeigen. | Einflussreiche Ausreißer können modellierte Regressionsbeziehungen von ihrer tatsächlichen optimalen Anpassung ablenken und Regressionskoeffizienten verzerren. | Erstellen Sie eine Scatterplotmatrix und andere Diagramme (Histogramme), um extreme Datenwerte zu untersuchen. Korrigieren oder entfernen Sie Ausreißer, wenn sie Fehler darstellen. Wenn es sich bei Ausreißern um richtige/gültige Werte handelt, können/sollten sie nicht entfernt werden. Führen Sie die Regression mit und ohne Ausreißer aus, um zu ermitteln, inwieweit sich dies auf die Ergebnisse auswirkt. |
Fehlende Stationarität. Möglicherweise werden Sie feststellen, dass eine Einkommensvariable in Region A sehr aussagekräftig ist, in Region B dagegen vernachlässigt werden kann oder gar das Vorzeichen wechselt. Abbildung anzeigen. | Wenn Beziehungen zwischen den abhängigen und erklärenden Variablen im Untersuchungsgebiet inkonsistent sind, werden berechnete Standardfehler künstlich vergrößert. | Das OLS-Werkzeug in ArcGIS testet automatisch, welche Probleme im Zusammenhang mit fehlender Stationarität (regionaler Variation) bestehen, und berechnet belastbare Standardfehlerwerte. Abbildung anzeigen. Wenn die Wahrscheinlichkeit in Zusammenhang mit dem Koenker-Test klein ist (z. B. < 0,05), liegt eine statistisch signifikante regionale Variation vor, und Sie sollten die robusten Wahrscheinlichkeiten heranziehen, um zu beurteilen, ob die erklärende Variable statistisch signifikant ist. Oft können die Modellergebnisse durch die Verwendung des Werkzeugs Geographisch gewichtete Regression verbessert werden. |
Multikollinearität. Eine oder eine Kombination von erklärenden Variablen ist redundant. Abbildung anzeigen. | Multikollinearität führt zu einer Verzerrung aufgrund von Überzählung und ergibt ein instabiles/unzuverlässiges Modell. | Das OLS-Werkzeug in ArcGIS überprüft automatisch, ob eine Redundanz vorliegt. Jeder erklärenden Variable wird ein berechneter VIF-Wert zugewiesen. Wenn dieser Wert groß ist (z. B. > 7,5), stellt Redundanz ein Problem dar, und die entsprechenden Variablen sollten aus dem Modell entfernt oder geändert werden, indem eine Interaktionsvariable erstellt oder die Beispielgröße vergrößert wird. Abbildung anzeigen. |
Inkonsistente Varianz bei Residuen. Es kann vorkommen, dass das Modell gute Vorhersagen für kleine Werte der abhängigen Variable ermöglicht, bei großen Werten jedoch unzuverlässig wird. Abbildung anzeigen. | Wenn das Modell einige Wertebereiche ungenau vorhersagt, sind die Ergebnisse verzerrt. | Das OLS-Werkzeug in ArcGIS testet automatisch, ob eine inkonsistente Residuenvarianz (als Heteroskedastizität bezeichnet) vorliegt, und berechnet Standardfehler, die Robustheit für dieses Problem zeigen. Wenn die Wahrscheinlichkeit in Zusammenhang mit dem Koenker-Test klein ist (z. B. < 0,05), sollten Sie die robusten Wahrscheinlichkeiten heranziehen, um zu beurteilen, ob die erklärende Variable statistisch signifikant ist. Abbildung anzeigen. |
Räumlich autokorrelierte Residuen. Abbildung anzeigen. | Wenn es eine räumliche Cluster-Bildung bei den zu niedrigen/zu hohen Vorhersagen des Modells gibt, wird eine Verzerrung aufgrund von Überzählung eingeführt, und das Modell ist unzuverlässig. | Führen Sie das Werkzeug Räumliche Autokorrelation für die Residuen aus, um sicherzustellen, dass es sich nicht um eine statistisch signifikante räumliche Cluster-Bildung handelt. Die statistisch signifikante räumliche Autokorrelation weist fast immer auf das Fehlen eines Wertes hin (eine wichtige Variable fehlt im Modell). Abbildung anzeigen. |
Normalverteilungsverzerrung. Abbildung anzeigen. | Wenn die Regressionsmodell-Residuen nicht mit einem Mittelwert von Null normal verteilt sind, erweisen sich die mit den Koeffizienten verknüpften P-Werte als unzuverlässig. | Das OLS-Werkzeug in ArcGIS testet automatisch, ob die Residuen normal verteilt sind. Wenn die Jarque-Bera-Statistik signifikant ist (z. B. < 0,05), enthält das Modell wahrscheinlich ungenügende Angaben (eine wichtige Variable fehlt im Modell) oder einige der modellierten Beziehungen sind nicht linear. Untersuchen Sie die ausgegebene Residuenkarte und ggf. GWR-Koeffizientenkarten, um festzustellen, ob dabei die in der Analyse fehlenden wichtigen Variablen erkennbar werden. Zeigen Sie Scatterplotmatrix-Diagramme an, und suchen Sie nach nicht linearen Beziehungen. |
Es ist wichtig, Tests im Hinblick auf alle oben aufgeführten Probleme auszuführen. Die Ergebnisse können zu 100 Prozent falsch (um 180 Grad abweichend) sein, wenn die oben beschriebenen Probleme ignoriert werden.
Räumliche Regression
Räumliche Daten enthalten zwei Eigenschaften, die es erschweren (jedoch nicht unmöglich machen), den Annahmen und Anforderungen herkömmlicher (nicht räumlicher) statistischer Methoden zu entsprechen:
- Geographische Features sind in den meisten Fällen räumlich zugeordnet. Das bedeutet, dass nahe beieinander liegende Features einander tendenziell ähnlicher sind als weiter entfernt liegende Features. Dadurch wird eine Überzählungsverzerrung für herkömmliche (nicht räumliche) Regressionsmethoden erstellt.
- Die Geographie ist wichtig, und oft sind die für Ihre Modellierung wichtigsten Prozesse nicht stationär. Diese Prozesse weisen in verschiedenen Teilen des Untersuchungsgebiets unterschiedliche Verhaltensweisen auf. Diese Eigenschaft räumlicher Daten kann als regionale Variation oder Nichtstationarität bezeichnet werden.
Wahre räumliche Regressionsmethoden wurden entwickelt, um diese beiden Eigenschaften von räumlichen Daten robust zu verwalten und selbst diese besonderen Qualitäten von räumlichen Daten einzubeziehen, um die Fähigkeit zum Modellieren von Datenbeziehungen zu verbessern. Einige räumliche Regressionsmethoden behandeln die erste Eigenschaft (räumliche Autokorrelation) effektiv, andere die zweite Eigenschaft (Nichtstationarität). Im Moment kann keine räumliche Regressionsmethode effektiv für beide Eigenschaften eingesetzt werden. Bei einem ordnungsgemäß spezifizierten GWR-Modell ist räumliche Autokorrelation normalerweise jedoch kein Problem.
Räumliche Autokorrelation
Es gibt anscheinend einen großen Unterschied zwischen der Betrachtungsweise der räumlichen Autokorrelation bei herkömmlichen Statistikern und räumlichen Statistikern. Der herkömmliche Statistiker betrachtet sie als negativen Faktor, der aus den Daten entfernt werden muss (z. B. durch Resampling), da die räumliche Autokorrelation gegen die zugrunde liegenden Annahmen vieler herkömmlicher (nicht räumlicher) statistischer Methoden verstößt. Für den Geographen oder GIS-Analysten ist räumliche Autokorrelation jedoch ein Beweis für wichtige zugrunde liegende räumliche Prozesse und ein integraler Bestandteil der Daten. Durch die Entfernung des Raums werden Daten ihres räumlichen Kontextes beraubt; das Ergebnis kann immer nur die halbe Wahrheit sein. Die in den Daten vorhandenen räumlichen Prozesse und räumlichen Beziehungen sind von entscheidendem Interesse und einer der Gründe dafür, dass die räumliche Datenanalyse für GIS-Benutzer so spannend ist. Um jedoch eine Verzerrung aufgrund von Überzählung in Ihrem Modell zu vermeiden, müssen Sie den vollständigen Satz erklärender Variablen ermitteln, anhand derer die inhärente räumliche Struktur in der abhängigen Variable erfasst werden kann. Wenn Sie nicht alle diese Variablen ermitteln können, wird sehr wahrscheinlich eine statistisch signifikante Autokorrelation in den Modellresiduen angezeigt. Unglücklicherweise sind die Regressionsergebnisse unzuverlässig, bis dieses Problem behoben ist. Testen Sie mit dem Werkzeug Räumliche Autokorrelation, ob in den Regressionsresiduen eine statistisch signifikante räumliche Autokorrelation vorliegt.
Es gibt mindestens drei Strategien, um Probleme im Zusammenhang mit räumlicher Autokorrelation in Regressionsmodell-Residuen zu lösen:
- Führen Sie ein Resampling durch, bis die Eingabevariablen keine statistisch signifikante räumliche Autokorrelation mehr aufweisen. Dadurch wird zwar nicht sichergestellt, dass die Analyse keine Probleme mit räumlicher Autokorrelation enthält, diese sind jedoch wesentlich unwahrscheinlicher, wenn die räumliche Autokorrelation aus den abhängigen und erklärenden Variablen entfernt wird. Dies ist der Ansatz des traditionellen Statistikers für den Umgang mit räumlicher Autokorrelation. Er ist nur geeignet, wenn die räumliche Autokorrelation das Ergebnis von Datenredundanz ist (das Referenzpunktschema ist zu fein).
- Isolieren Sie die räumlichen und nicht räumlichen Komponenten der einzelnen Eingabevariablen mithilfe einer räumlichen Filterregressionsmethode. Der Raum wird aus den einzelnen Variablen entfernt, jedoch als neue Variable wieder in das Regressionsmodell zurückgebracht, um räumliche Effekte/die räumliche Struktur zu berücksichtigen. ArcGIS stellt momentan keine räumlichen Filterregressionsmethoden bereit.
- Beziehen Sie die räumliche Autokorrelation anhand von räumlichen Ökonometrie-Regressionsmethoden in das Regressionsmodell mit ein. Räumliche Ökonometrie-Regressionsmethoden werden in einer zukünftigen Version in ArcGIS vorhanden sein.
Regionale Variation
Bei globalen Modellen wie der OLS-Regression werden Gleichungen erstellt, mit denen die allgemeinen Datenbeziehungen in einem Untersuchungsgebiet am besten beschrieben werden. Wenn diese Beziehungen im Untersuchungsgebiet konsistent sind, werden diese Beziehungen mit der OLS-Regressionsgleichung gut modelliert. Verhalten sich diese Beziehungen in verschiedenen Teilen des Untersuchungsgebiets jedoch unterschiedlich, ist die Regressionsgleichung eher ein Durchschnitt der vorhandenen Beziehungen. Wenn diese Beziehungen dabei zwei Extreme darstellen, wird der globale Durchschnitt keines der Extreme gut darstellen. Wenn die erklärenden Variablen nicht stationäre Beziehungen (regionale Varianz) aufweisen, tendieren globale Modelle dazu fehlzuschlagen, sofern keine robusten Methoden zum Berechnen der Regressionsergebnisse verwendet werden. Idealerweise können Sie einen vollständigen Satz erklärender Variablen identifizieren, um die der abhängigen Variable innewohnende regionale Variation zu erfassen. Wenn Sie jedoch nicht alle diese räumlichen Variablen ermitteln können, werden Sie erneut eine statistisch signifikante Autokorrelation in den Modellresiduen und/oder den R-Squared-Werten feststellen, die niedriger als erwartet sind. Unglücklicherweise sind die Regressionsergebnisse unzuverlässig, bis dieses Problem behoben ist.
Es gibt mindestens vier Möglichkeiten, Probleme mit regionaler Variation in OLS-Regressionsmodellen zu lösen:
- Beziehen Sie eine Variable in das Modell mit ein, das die regionale Variation erklärt. Wenn Sie feststellen, dass für Ihr Modell im Norden stets zu hohe und im Süden stets zu niedrige Werte vorhergesagt werden, fügen Sie beispielsweise eine regionale Variable mit der Einstellung 1 für Features im Norden und 0 für Features im Süden hinzu.
- Verwenden Sie Methoden, die die regionale Variation in das Regressionsmodell einbeziehen, z. B. die geographisch gewichtete Regression.
- Konsultieren Sie robuste Regressionsstandardfehler und -wahrscheinlichkeiten, um zu bestimmen, ob Variablenkoeffizienten statistisch signifikant sind. Weitere Informationen finden Sie unter Interpretieren der Ergebnisse der OLS-Regression. Die geographisch gewichtete Regression wird dennoch empfohlen.
- Definieren Sie die Größe des Untersuchungsgebiets neu bzw. reduzieren Sie sie, damit alle Prozesse darin stationär sind (und keine regionale Variation mehr aufweisen).
Weitere Informationen zum Verwenden der Regressionswerkzeuge finden Sie in den folgenden Themen:
Weitere Informationen zur OLS-Regression
Weitere Informationen zur GWR-Regression