Die Regressionsanalyse dient dazu, komplexe Phänomene zu verstehen, zu modellieren, vorherzusagen und/oder zu erklären. Sie hilft bei der Beantwortung von Fragen wie: "Warum liegen die Prüfungsergebnisse von Schülern in einigen Orten der USA ständig über dem nationalen Durchschnitt?" oder "Warum ist in einigen Stadtteilen die Rate der Wohnungseinbrüche so hoch?" Mit einer Regressionsanalyse können Sie beispielsweise Fettleibigkeit bei Kindern erklären, indem Sie einen Satz verwandter Variablen wie z. B. Einkommen, Bildung und Zugang zu gesunden Lebensmitteln verwenden.
In der Regel hilft Ihnen eine Regressionsanalyse dabei, diese Warum-Fragen zu beantworten, sodass Sie etwas gegen die Ursache unternehmen können. Wenn Sie beispielsweise feststellen, dass Kinder in Schulen, in denen es zum Mittagessen frisches Obst und Gemüse gibt, weniger zu Fettleibigkeit neigen, können Sie diese Informationen zur Strategieplanung verwenden und Entscheidungen bezüglich Mittagessensprogrammen in Schulen treffen. Entsprechend können Sie – wenn Sie die Variablen kennen, die hohe Kriminalitätsraten erklären – Vorhersagen zu zukünftigen Straftaten machen, sodass effektivere Präventionsmaßnahmen ergriffen werden können.
Diese Verwendungsmöglichkeiten der Regressionsanalyse sind allgemein bekannt.
Was beim Thema Regressionsanalyse jedoch gern unerwähnt bleibt, ist die Tatsache, dass es nicht immer ganz leicht ist, einen Satz erklärender Variablen zu finden, mit denen eine Frage beantwortet oder das zu modellierende komplexe Phänomen verständlich gemacht werden kann. Fettleibigkeit bei Kindern, Kriminalität, Prüfungsergebnisse und nahezu alle Themen, die mit der Regressionsanalyse modelliert werden können, sind komplizierte Fragen, auf die es selten eine einfache Antwort gibt. Wenn Sie schon einmal versucht haben, ein eigenes Regressionsmodell zu erstellen, wird Ihnen diese Problematik vermutlich nicht neu sein.
Glücklicherweise wird Ihnen bei Ausführung des Regressionswerkzeugs Kleinste Quadrate (Ordinary Least Squares, OLS) eine Reihe von Diagnoseoptionen angeboten, mit deren Hilfe Sie feststellen können, ob Ihr Modell ordnungsgemäß spezifiziert ist; ein ordnungsgemäß spezifiziertes Modell ist vertrauenswürdig. In diesem Dokument werden die sechs Prüfungen erläutert, mit denen Sie die Vertrauenswürdigkeit eines Modells feststellen können. Diese sechs Prüfungen sowie die Techniken zur Lösung einiger gängiger Probleme im Zusammenhang mit Regressionsanalysen sind Ressourcen, die Ihnen die Arbeit erheblich erleichtern.
Erste Schritte
Als Erstes wählen Sie die Variable aus, die Sie verstehen, vorhersagen oder modellieren möchten. Diese Variable wird als abhängige Variable bezeichnet. Fettleibigkeit bei Kindern, Kriminalität und Prüfungsergebnisse sind die abhängigen Variablen, die in den vorstehend beschriebenen Beispielen modelliert werden.
Als Nächstes müssen Sie überlegen, mit welchen Faktoren die abhängige Variable erklärt werden könnte. Diese Variablen werden als erklärende Variablen bezeichnet. Im Beispiel der Fettleibigkeit bei Kindern sind erklärende Variablen z. B. Einkommen, Bildung und Zugang zu gesunden Lebensmitteln. Hier müssen Sie recherchieren, um alle erklärenden Variablen zu identifizieren, die wichtig sein könnten; lesen Sie theoretische Abhandlungen und vorhandene Literatur, sprechen Sie mit Experten, und verlassen Sie sich stets auf Ihren gesunden Menschenverstand. Wenn Sie im Vorfeld sorgfältig recherchieren, steigen Ihre Chancen, ein geeignetes Modell zu finden, erheblich.
Nachdem Sie die abhängige Variable festgelegt und die potenziellen erklärenden Variablen ausgewählt haben, können Sie die Analyse ausführen. Beginnen Sie eine Regressionsanalyse immer mit dem Werkzeug Kleinste Quadrate (Ordinary Least Squares, OLS) oder Regressionsanalyse, da diese Werkzeuge wichtige Diagnosetests durchführen, deren Ergebnis Ihnen sagt, ob Ihr Modell geeignet ist oder Sie noch weiter daran arbeiten müssen.
Das OLS-Werkzeug generiert mehrere Ausgaben, darunter eine Karte der Regressionsresiduen und einen Zusammenfassungsbericht. Die Karte der Regressionsresiduen zeigt die zu niedrigen oder zu hohen Vorhersagen aus dem Modell; die Analyse dieser Karte ist ein wichtiger Schritt bei der Suche nach einem geeigneten Modell. Der Zusammenfassungsbericht erhält größtenteils Zahlen und umfasst alle Diagnosen, die Sie bei der Durchführung der unten aufgeführten sechs Prüfungen verwenden.
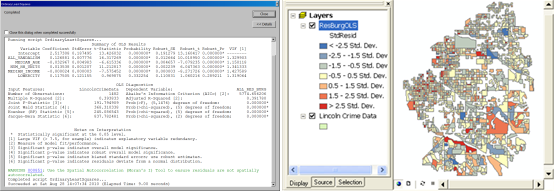
Die sechs Prüfungen
Prüfung 1: Sind diese erklärenden Variablen für mein Modell hilfreich?
Nachdem Sie Theorie und vorhandene Rechercheergebnisse zu Rate gezogen haben, verfügen Sie über einen Satz potenzieller erklärender Variablen. Sie haben gute Gründe, diese in das Modell aufzunehmen. Nach Ausführung des Modells werden Sie jedoch feststellen, dass einige der erklärenden Variablen statistisch signifikant sind und andere nicht.
Wie erkennen Sie, welche erklärenden Variablen signifikant sind? Das OLS-Werkzeug berechnet für jede erklärende Variable im Modell einen Koeffizienten und führt einen statistischen Test durch, um festzustellen, ob die Variable für das Modell hilfreich ist oder nicht. Mit dem statistischen Test wird die Wahrscheinlichkeit berechnet, dass der Koeffizient tatsächlich null ist. Wenn der Koeffizient null (oder sehr nahe null) ist, ist die zugehörige erklärende Variable für das Modell nicht hilfreich. Wenn der statistische Test eine geringe Wahrscheinlichkeit (einen kleinen p-Wert) für eine bestimmte erklärende Variable zurückgibt, weist dies hingegen darauf hin, dass es unwahrscheinlich ist (nur eine geringe Wahrscheinlichkeit besteht), dass der Koeffizient null ist. Wenn die Wahrscheinlichkeit kleiner als 0,05 ist, zeigt ein Sternchen neben der Wahrscheinlichkeit im OLS-Zusammenfassungsbericht an, dass die zugehörige erklärende Variable für das Modell wichtig ist (anders ausgedrückt, der entsprechende Koeffizient ist auf dem Konfidenzniveau von 95 Prozent statistisch signifikant). Sie sollten also nach erklärenden Variablen suchen, die mit statistisch signifikanten Wahrscheinlichkeiten verknüpft sind (suchen Sie nach Wahrscheinlichkeiten mit Sternchen).
Das OLS-Werkzeug berechnet die Wahrscheinlichkeit und die robuste Wahrscheinlichkeit für jede erklärende Variable. Bei räumlichen Daten ist es nicht ungewöhnlich, dass die zu modellierenden Beziehungen innerhalb des Untersuchungsgebiets variieren. Diese Beziehungen sind als nichtstationär charakterisiert. Im Fall von nichtstationären Beziehungen geben nur robuste Wahrscheinlichkeiten zuverlässig Auskunft darüber, ob eine erklärende Variable statistisch signifikant ist.
Wie stellen Sie fest, ob die Beziehungen im Modell nichtstationär sind? Als weiteren statistischen Test enthält der OLS-Zusammenfassungsbericht die Koenker-Statistik (Koenkers t-verteilte Breusch-Pagan-Statistik) für Nichtstationarität. Ein Sternchen neben dem p-Wert der Koenker-Statistik zeigt an, dass die modellierten Beziehungen eine statistisch signifikante Nichtstationarität aufweisen; achten Sie in diesem Fall darauf, die robusten Wahrscheinlichkeiten zu betrachten.
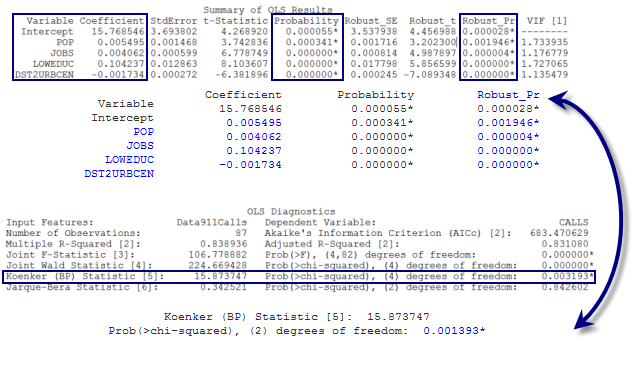
In der Regel empfiehlt es sich, nicht statistisch signifikante erklärende Variablen aus dem Modell zu entfernen. Wenn die Theorie jedoch besagt, dass ein Variable sehr wichtig ist, oder wenn eine bestimmte Variable im Zentrum der Analyse steht, können Sie sie auch dann behalten, wenn sie nicht statistisch signifikant ist.
Prüfung 2: Entsprechen die Beziehungen meinen Erwartungen?
Es ist nicht nur wichtig zu ermitteln, ob eine erklärende Variable tatsächlich für das Modell hilfreich ist, sondern auch, das Vorzeichen (+/-) der einzelnen Koeffizienten zu überprüfen, um sicherzustellen, dass die Beziehung den Erwartungen entspricht. Das Vorzeichen des Koeffizienten einer erklärenden Variablen gibt an, ob die Beziehung positiv oder negativ ist. Angenommen, Sie modellieren beispielsweise Kriminalität, und eine der erklärenden Variablen ist das Durchschnittseinkommen der Nachbarschaft. Ist der Koeffizient für die Einkommensvariable eine negative Zahl, bedeutet dies, dass die Kriminalität mit steigenden Nachbarschaftseinkommen tendenziell abnimmt (negative Beziehung). Wenn Sie Fettleibigkeit bei Kindern modellieren und die Variable "Zugang zu Fast-Food" einen positiven Koeffizienten hat, weist dies darauf hin, dass Fettleibigkeit bei Kindern tendenziell zunimmt, wenn der Zugang zu Fast-Food zunimmt (positive Beziehung).
Bei Erstellung der Liste potenzieller erklärender Variablen sollten Sie für jede Variable auch die erwartete Beziehung (positiv oder negativ) angeben. Wenn ein Modell Beziehungen ausgibt, die weder der Theorie noch dem gesunden Menschenverstand entsprechen, sollten Sie diesem nicht trauen; andernfalls könnte es zu erheblichen Problemen kommen. Angenommen, Sie erstellen ein Modell, um die Häufigkeit von Waldbränden vorherzusagen, und das Regressionsmodell gibt einen positiven Koeffizienten für die Niederschlagsvariable zurück. Sie gehen vermutlich nicht davon aus, dass in regenreichen Gegenden eine Zunahme von Waldbränden zu erwarten ist.
Unerwartete Vorzeichen von Koeffizienten weisen häufig auf andere Probleme mit dem Modell hin, die zutage treten, wenn Sie die sechs Prüfungen weiter durcharbeiten. Sie können dem Vorzeichen und der Aussagekraft der Koeffizienten von erklärenden Variablen nur vertrauen, wenn das Modell alle Prüfungen besteht. Wenn ein Modell trotz des unerwarteten Koeffizientenvorzeichens alle Prüfungen besteht, ist dies möglicherweise eine Gelegenheit für Sie, etwas Neues zu lernen. Vielleicht ist die Beziehung zwischen Waldbrandhäufigkeit und Niederschlag deshalb positiv, weil die primäre Ursache von Waldbränden im Untersuchungsgebiet Blitzeinschläge sind. Es kann sich lohnen, Daten über Gewitter in Ihrem Untersuchungsgebiet einzuholen, um festzustellen, ob sich hierdurch die Modell-Performance verbessert.
Prüfung 3: Gibt es redundante erklärende Variablen?
Suchen Sie bei der Auswahl von erklärenden Variablen für Ihre Analyse nach Variablen, die unterschiedliche Aspekte des zu modellierenden Phänomens ansprechen; vermeiden Sie Variablen mit identischer Aussage. Wenn Sie beispielsweise Wohnungswerte modellieren, nehmen Sie vermutlich nicht sowohl die Wohnfläche als auch die Anzahl der Schlafzimmer als erklärende Variablen auf. Beide Variablen beziehen sich auf die Größe der Wohnung, und die Aufnahme beider Variablen in das Modell könnte dieses instabil machen. Letztendlich können Sie einem Modell mit redundanten Variablen nicht vertrauen.
Wie erkennen Sie, ob zwei oder mehr erklärende Variablen redundant sind? Wenn mehr als zwei erklärende Variablen vorliegen, wird vom OLS-Werkzeug ein Varianzinflationsfaktor (Variance Inflation Factor, VIF) für jede Variable berechnet. Der VIF-Wert ist ein Messwert der Variablenredundanz und kann dabei helfen zu entscheiden, welche Variablen aus dem Modell entfernt werden können, ohne die Aussagekraft zu gefährden. Als Faustregel gilt, dass ein VIF-Wert über 7,5 problematisch ist. Wenn zwei oder mehr Variablen einen VIF-Wert über 7,5 aufweisen, sollten Sie diese nacheinander entfernen und das OLS-Werkzeug erneut ausführen, bis keine Redundanz mehr aufgezeigt wird. Denken Sie daran, dass nicht notwendigerweise alle Variablen mit hohen VIF-Werten entfernt werden müssen. Im Beispiel zur Modellierung von Wohnungswerten haben vermutlich sowohl die Wohnfläche als auch die Anzahl der Schlafzimmer eine übermäßig hohen VIF-Wert. Sobald Sie jedoch eine dieser beiden Variablen entfernen, liegt keine Redundanz mehr vor. Die Aufnahme einer Variablen für die Wohnungsgröße ist wichtig, allerdings soll dieser Aspekt von Wohnungswerten nicht redundant modelliert werden.
Prüfung 4: Hat das Modell eine Tendenz?
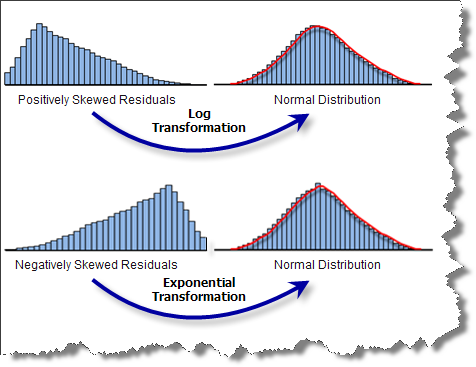
Diese Frage scheint kompliziert, die Antwort darauf ist jedoch sehr einfach. Bei einem ordnungsgemäß spezifizierten OLS-Modell sind die Modellresiduen (die zu hohen und zu niedrigen Vorhersagen) normal verteilt und haben einen Mittelwert von null (Glockenkurve). Wenn das Modell jedoch eine Tendenz hat (verzerrt ist), ist die Verteilung der Residuen unausgewogen, wie in der folgenden Abbildung dargestellt. Bei Vorliegen einer Modelltendenz können Sie den vorhergesagten Ergebnisse nicht vollständig vertrauen. Zum Glück gibt es verschiedene Strategien, mit denen Sie dieses Problem lösen können.
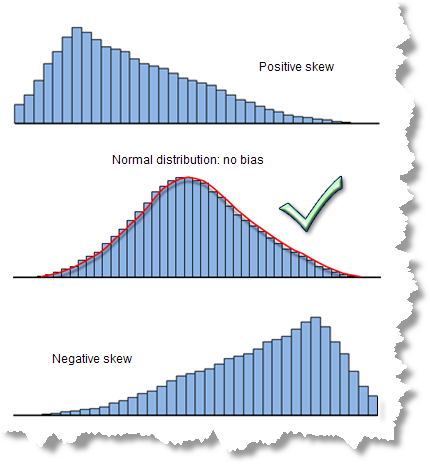
Eine statistisch signifikante Jarque-Bera-Diagnose (suchen Sie nach dem Sternchen) weist auf eine Modelltendenz hin. Manchmal funktioniert ein Modell für niedrige Werte gut, für hohe Werte jedoch stimmen die Vorhersagen nicht (oder umgekehrt). Beim Beispiel der Fettleibigkeit bei Kindern würde dies bedeuten, dass das Modell in Gegenden mit geringer Fettleibigkeit bei Kindern gut funktioniert, in Gegenden mit hoher Fettleibigkeit bei Kindern die Vorhersagen jedoch nicht zutreffend sind. Eine Modelltendenz kann auch das Ergebnis von Ausreißern sein, die die Modellschätzung beeinflussen.
Zur Behebung der Modelltendenz können Sie eine Scatterplotmatrix für alle Modellvariablen erstellen. Ein häufige Ursache für Modelltendenz ist eine nichtlineare Beziehung zwischen der abhängigen Variablen und einer der erklärenden Variablen. In der Scatterplotmatrix sieht diese Beziehung wie eine geschwungene Linie aus. Lineare Beziehungen werden als diagonale Linien dargestellt.
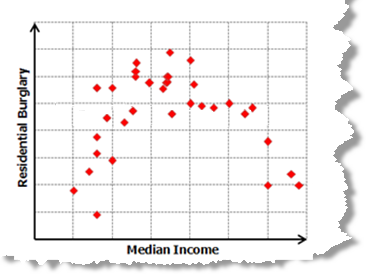
Wenn zwischen der abhängigen Variablen und einer der erklärenden Variablen eine nichtlineare Beziehung besteht, müssen Sie etwas dagegen unternehmen. OLS ist eine lineare Regressionsmethode, die davon ausgeht, dass die modellierten Beziehungen linear sind. Wenn dies nicht der Fall ist, können Sie versuchen, die Variablen zu transformieren, um festzustellen, ob hierdurch linearere Beziehungen entstehen. Zu den gängigen Transformationen gehören Logarithmus- und Exponentialfunktion. Aktivieren Sie die Option Histogramme anzeigen im Assistenten "Scatterplotmatrix-Diagramm erstellen", um für jede Variable in der Scatterplotmatrix ein Histogramm aufzunehmen. Falls einige der erklärenden Variablen stark verzerrt sind, können Sie die Modelltendenz möglicherweise entfernen, indem Sie diese ebenfalls transformieren.
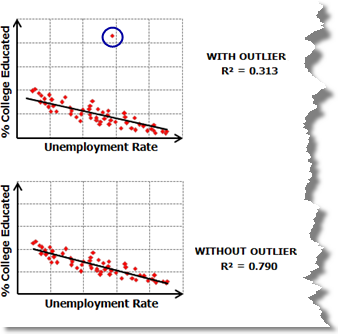
Die Scatterplotmatrix zeigt auch Datenausreißer auf. Um festzustellen, ob das Modell durch einen Ausreißer beeinflusst wird, führen Sie OLS einmal mit und einmal ohne Ausreißer aus, und überprüfen Sie, inwieweit sich hierdurch die Modell-Performance ändert und ob durch Entfernen des Ausreißers die Modelltendenz behoben wird. In einigen Fällen (vor allem wenn die Ausreißer Ihrer Meinung nach fehlerhafte Daten darstellen), können Sie die Ausreißer eventuell aus der Analyse entfernen.
Prüfung 5: Wurden alle wichtigen erklärenden Variablen ermittelt?
Häufig starten Sie eine Analyse mit Hypothesen über die Variablen, die gute Vorhersagen ermöglichen. Sie glauben vielleicht, dass mit fünf bestimmten Variablen ein gutes Modell erstellt werden kann; vielleicht haben Sie auch eine feste Liste mit zehn Variablen, die Ihrer Meinung nach relevant sind. Es ist zwar wichtig, zu Beginn einer Regressionsanalyse eine Hypothese aufzustellen, genauso wichtig ist es jedoch, mit Kreativität und auf Basis gewonnener Erkenntnisse weiterzusuchen. Widerstehen Sie der Neigung, sich auf die ursprüngliche Variablenliste zu beschränken, und versuchen Sie, alle möglichen Variablen zu berücksichtigen, die sich auf das zu modellierende Thema auswirken könnten. Erstellen Sie thematische Karten jeder potenziellen erklärenden Variablen, und vergleichen Sie diese mit einer Karte der abhängigen Variablen. Gehen Sie noch einmal die einschlägige Literatur durch. Nutzen Sie Ihre Intuition, und suchen Sie nach Beziehungen in den kartierten Daten. Versuchen Sie unbedingt, so viele potenzielle räumliche Variablen wie möglich zu identifizieren, wie beispielsweise die Entfernung vom Stadtzentrum, die Nähe zu wichtigen Fernstraßen oder der Zugang zu großen Gewässern. Diese Art von Variablen ist besonders für Analysen wichtig, bei denen Sie davon ausgehen, dass geographische Prozesse die Beziehungen zwischen den Daten beeinflussen. Bis Sie erklärende Variablen gefunden haben, die die räumliche Struktur in der abhängigen Variable effektiv erfassen, fehlen dem Modell tatsächlich wichtige erklärende Variablen, und nicht alle der hier beschriebenen Diagnoseprüfungen können erfolgreich durchgeführt werden.
Eine statistisch signifikante räumliche Autokorrelation der Modellresiduen ist ein Zeichen dafür, dass in dem Modell mindestens eine wichtige erklärende Variable fehlt. In der Regressionsanalyse treten Probleme mit räumlich autokorrelierten Residuen in der Regel in Form einer Cluster-Bildung auf: Die zu hohen Vorhersagen bilden ein Cluster, und die zu niedrigen Vorhersagen bilden ein Cluster. Wie erkennen Sie, ob die Modellresiduen eine statistisch signifikante räumliche Autokorrelation aufweisen? Führen Sie das Werkzeug Räumliche Autokorrelation für die Regressionsresiduen aus, um herauszufinden, ob ein Problem mit räumlicher Autokorrelation vorliegt. Ein statistisch signifikanter Z-Score weist darauf hin, dass wichtige erklärende Variablen im Modell fehlen.
Diese fehlenden erklärenden Variablen zu finden, ist häufig eher eine Kunst als eine Wissenschaft. Versuchen Sie, ob die nachfolgenden Strategien hilfreich sind:
Untersuchen der OLS-Residuenkarte
Die OLS-Standardausgabe ist eine Karte der Modellresiduen. Rote Bereiche zeigen an, dass die tatsächlichen Werte (die abhängige Variable) größer sind als vom Modell vorhergesagt. Blaue Bereiche zeigen an, dass die tatsächlichen Werte niedriger als die Vorhersage sind. Manchmal gibt Ihnen schon ein kurzer Blick auf die Residuenkarte einen Hinweis darauf, was möglicherweise fehlt. Wenn Sie beispielsweise feststellen, dass Ihre Vorhersagen in städtischen Gebieten ständig zu hoch sind, könnte sich die Hinzufügung einer Variablen empfehlen, die die Entfernung zum Stadtzentrum darstellt. Wenn zu hohe Vorhersagen mit Berggipfeln oder Talsohlen in Zusammenhang zu stehen scheinen, benötigen Sie möglicherweise eine Höhenvariable. Werden regionale Cluster angezeigt, oder sind Trends in den Daten zu erkennen? Wenn dies der Fall ist, kann möglicherweise die Erstellung einer Dummy-Variablen zur Erfassung dieser regionalen Unterschiede helfen. Das klassische Beispiel einer Dummy-Variablen ist eine Variable, die städtische und ländliche Features unterscheidet. Indem Sie allen ländlichen Features den Wert 1 und allen übrigen Features den Wert 0 zuweisen, können Sie räumliche Beziehungen in der Landschaft erfassen, die möglicherweise für das Modell wichtig sind. Manchmal hilft auch die Erstellung einer Hot-Spot-Karte von Modellresiduen dabei, umfangreiche regionale Muster zu visualisieren.
Durch Ermitteln der fehlenden räumlichen Variablen können Sie nicht nur das Modell verbessern, sondern dieser Prozess kann auch zu einem besseren Verständnis des modellierten Phänomens mit neuen und innovativen Methoden beitragen.
Untersuchen der Nichtstationarität
Sie können auch versuchen, das Werkzeug Geographisch gewichtete Regression auszuführen und Koeffizientenoberflächen für jede der erklärenden Variablen und/oder Karten der lokalen R2-Werte zu erstellen. Wählen Sie das gut funktionierende OLS-Modell aus (eines mit einem hohen Adjusted R2-Wert, das alle oder die meisten der übrigen Diagnoseprüfungen besteht). Da GWR eine Regressionsgleichung für jedes Feature im Untersuchungsgebiet erstellt, veranschaulichen die Koeffizientenoberflächen, wie die Beziehungen zwischen der abhängigen Variablen und den einzelnen erklärenden Variablen geographisch fluktuieren; die Karte lokaler R2-Werte zeigt Variationen in der Aussagekraft des Modells. Manchmal gibt die Betrachtung dieser geographischen Variationen einen Anhaltspunkt, welche Variablen fehlen könnten: Eine verminderte Aussagekraft in der Nähe wichtiger Autobahnen, ein Rückgang mit der Entfernung von der Küste, eine Änderung des Koeffizientenvorzeichens in der Nähe eines Industriegebiets oder ein deutlicher Ost-West-Trend oder eine Grenze – all dies sind Hinweise auf räumliche Variablen, die das Modell verbessern können.
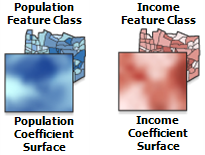
Achten Sie bei der Untersuchung der Koeffizientenoberflächen auf erklärende Variablen mit Koeffizienten, deren Vorzeichen sich von positiv in negativ ändert. Dies ist wichtig, weil OLS das Vorhersagepotenzial dieser extrem nichtstationären Variablen vermutlich unberücksichtigt lässt. Betrachten Sie beispielsweise die Beziehung zwischen Fettleibigkeit bei Kindern zu Zugang zu gesunden Lebensmitteln. Möglicherweise ist in Gebieten mit niedrigem Einkommen und weniger Autos eine große Entfernung zu einem Supermarkt ein echtes Hindernis bei der Entscheidung für gesunde Lebensmittel. In Gebieten mit hohem Einkommen und mehr Autos jedoch ist möglicherweise ein fußläufig erreichbarer Supermarkt gar nicht wünschenswert; die Entfernung zum Supermarkt stellt eventuell gar kein Hindernis für den Kauf gesunder Lebensmittel dar. GWR kann diese Arten komplexer Beziehungen modellieren, OLS hingegen nicht. OLS ist ein globales Modell und geht davon aus, dass Variablenbeziehungen innerhalb des Untersuchungsgebiets konsistent (stationär) sind. Wenn sich das Vorzeichen von Koeffizienten ändert, heben sich die Koeffizienten gegenseitig auf. Stellen Sie sich dies wie (+1) + (-1) = 0 vor. Wenn Sie Variablen finden, deren Koeffizienten sich dramatisch ändern, insbesondere wenn sich ihr Vorzeichen ändert, sollten Sie diese im Modell belassen, auch wenn sie nicht statistisch signifikant sind. Diese Arten von Variablen zeigen beim Wechsel zu GWR Wirkung.
Anpassen von OLS an kleinere Teiluntersuchungsgebiete
GWR ist bei der Verarbeitung von Nichtstationarität sehr nützlich, und Sie könnten versucht sein, direkt zu GWR zu wechseln, ohne zunächst ein ordnungsgemäß spezifiziertes OLS-Modell zu entwickeln. Leider verfügt GWR nicht über die hervorragenden Diagnoseoptionen, mit denen Sie herausfinden können, ob die erklärenden Variablen statistisch signifikant sind, ob die Residuen normal verteilt sind oder – letztendlich – ob Ihr Modell ein gutes Modell ist. Mit GWR kann ein nicht ordnungsgemäß spezifiziertes Modell nur dann korrigiert werden, wenn Sie sicher sind, dass das OLS-Modell die sechs Prüfungen ausschließlich aufgrund von Nichtstationarität nicht besteht. Das Vorliegen von Nichtstationarität ist dann nachgewiesen, wenn Sie erklärende Variablen finden, die in einigen Teilen des Untersuchungsgebiets eine starke positive Beziehung und in anderen Teilen eine starke negative Beziehung aufweisen. Manchmal wird das Problem nicht durch einzelne erklärende Variablen verursacht, sondern durch den im Modell verwendeten Satz erklärender Variablen. Möglicherweise liefert ein Satz Variablen ein hervorragendes Modell für einen Teil des Untersuchungsgebiets, in anderen Teilen funktioniert jedoch ein Satz anderer Variablen am besten. Um dies zu überprüfen, können Sie mehrere kleine Teiluntersuchungsgebiete auswählen und versuchen, OLS-Modelle an jedes davon anzupassen. Wählen Sie die Teilgebiete basierend auf den Prozessen aus, die Ihrer Meinung nach mit Ihrem Modell in Beziehung stehen (Gebiete mit hohem und niedrigem Einkommen, alte und neue Wohnungen). Wählen Sie alternativ Gebiete basierend auf der GWR-Karte lokaler R2-Werte aus; die Orte mit schlechter Modell-Performance können möglicherweise mit einem anderen Satz erklärender Variablen besser modelliert werden.
Wenn Sie in mehreren kleinen Untersuchungsgebieten ordnungsgemäß spezifizierte OLS-Modelle finden, können Sie daraus schließen, dass Nichtstationarität die Problemursache ist, und den vollen Satz erklärender Variablen aus allen Teilgebietmodellen in GWR übernehmen. Wenn Sie in den kleineren Teilgebieten keine ordnungsgemäß spezifizierten Modelle finden, versuchen Sie möglicherweise ein Phänomen zu modellieren, das zu komplex ist, um es auf eine einfache Reihe numerischer Messungen und linearer Beziehungen zu reduzieren. In diesem Fall müssen Sie sich wahrscheinlich nach alternativen Analysemethoden umsehen.
All dies kann recht arbeitsaufwändig sein, es ist jedoch auch eine gute Übung in der Analyse erklärender Daten und hilft Ihnen dabei, Ihre Daten besser zu verstehen und neue Variablen zu finden; möglicherweise kommt am Ende sogar ein hervorragendes Modell heraus.
Prüfung 6: Wie gut wird die abhängige Variable erklärt?
Im letzten Schritt wird nun endlich die Modell-Performance bewertet. Der Adjusted R2-Wert ist ein wichtiger Messwert dafür, wie gut die erklärenden Variablen die abhängige Variable modellieren. Der R2-Wert ist außerdem einer der ersten Aspekte, die Sie über die Regressionsanalyse lernen. Warum also kommt diese wichtige Prüfung erst ganz zum Schluss? Was Ihnen nicht erklärt wird ist, dass Sie dem R2-Wert nur dann vertrauen können, wenn alle anderen oben genannten Prüfungen erfolgreich bestanden wurden. Wenn Ihr Modell eine Tendenz aufweist, kann es in einigen Gebieten oder mit einem bestimmten Bereich der abhängigen Variablenwerte gut funktionieren, in allen anderen Situationen aber völlig fehlschlagen. Der R2-Wert spiegelt dies nicht wider. Entsprechend können Sie bei Residuen mit räumlicher Autokorrelation den Koeffizientenbeziehungen des Modells nicht trauen. Bei redundanten erklärenden Variablen können die R2-Werte extrem hoch sein, das Modell ist jedoch instabil; es spiegelt nicht die tatsächlichen Beziehungen wider, die Sie zu modellieren versuchen, und führt bei Hinzufügung selbst einer einzigen Beobachtung möglicherweise zu komplett anderen Ergebnissen.
Nachdem Sie die übrigen Prüfungen durchgeführt haben und sicher sind, dass alle erforderlichen Kriterien erfüllt wurden, ist es jedoch an der Zeit festzustellen, wie gut das Modell die Werte für die abhängige Variable erklärt, indem der Adjusted R2-Wert bewertet wird. R2-Werte liegen im Bereich zwischen 0 und 1 und stellen einen Prozentsatz dar. Angenommen, Sie modellieren Kriminalitätsraten und finden ein Modell, das die vorherigen fünf Prüfungen besteht und einen Adjusted R2-Wert von 0,65 aufweist. Dies sagt Ihnen, dass die erklärenden Variablen im Modell die Kriminalitätsrate zu 65 Prozent erklären (technischer ausgedrückt, das Modell erklärt 65 Prozent der Variation in der abhängigen Variable "Kriminalitätsrate"). Adjusted R2-Werte müssen eher subjektiv bewertet werden. In einigen Wissenschaftsbereichen ist die Erklärung von 23 Prozent eines komplexen Phänomens ein hervorragendes Ergebnis. In anderen Bereichen muss ein R2-Wert näher an 80 oder 90 Prozent liegen, um überhaupt Beachtung zu finden. So oder so, der Adjusted R2-Wert hilft Ihnen dabei, die Performance Ihres Modells zu bewerten.
Eine weitere wichtige Diagnosefunktion, die Sie bei der Bewertung der Modell-Performance unterstützt, ist das korrigierte Akaike's Information Criterion (AICc). Der AICc-Wert ist ein hilfreicher Messwert für den Vergleich mehrerer Modelle. Sie können beispielsweise die Prüfungsergebnisse von Schülern mit verschiedenen Sätzen von erklärenden Variablen modellieren. In einem Modell verwenden Sie nur demografische Variablen, in einem anderen Modell wählen Sie Variablen aus, die sich auf die Schule und das Klassenzimmer beziehen, z. B. Ausgaben pro Schüler und Lehrer-Schüler-Verhältnis. Solange für alle verglichenen Modelle die gleiche abhängige Variable verwendet wird (in diesem Fall Prüfungsergebnisse der Schüler), können Sie die Performance der Modelle mithilfe der AICc-Werte vergleichen. Das Modell mit dem niedrigeren AICc-Wert ist besser an die beobachteten Daten angepasst.
Denken Sie daran. . .
Denken Sie bei der Durcharbeitung der Schritte zur Erstellung eines ordnungsgemäß spezifizierten Regressionsmodells daran, dass Ihre Analyse das Ziel hat, die Daten zu verstehen und anhand dieser Erkenntnisse Probleme zu lösen und Fragen zu beantworten. Tatsächlich kann es passieren, dass Sie eine ganze Reihe von Modellen ausprobieren (mit und ohne transformierte Variablen), mehrere kleine Untersuchungsbiete betrachten, Koeffizientenoberflächen analysieren ... ohne ein ordnungsgemäß spezifiziertes OLS-Modell zu finden. Aber – und das ist wichtig – Sie leisten trotzdem einen Beitrag zu den gesammelten Erkenntnissen über das modellierte Phänomen. Fall sich das Modell, dass in Ihrer Hypothese hervorragende Vorhersagen ermöglicht, als überhaupt nicht signifikant herausstellt, ist auch diese Erkenntnis eine sehr wertvolle Information. Falls eine der Variablen, die Sie als besonders aussagekräftig eingestuft hatten, in einigen Gebieten eine positive Beziehung und in anderen eine negative aufweist, trägt dieses Wissen mit Sicherheit zu einem besseren Verständnis des Problems bei. Alle Arbeit, die Sie hier investieren, um mithilfe von OLS ein funktionierendes Modell zu ermitteln und dann durch Anwendung von GWR regionale Variationen zwischen den Modellvariablen zu untersuchen, wird immer von Nutzen sein.
Weitere Informationen zur Regressionsanalyse finden Sie auf der Seite Spatial Statistics Resources.