Disponible avec une licence Geostatistical Analyst.
Une des décisions les plus importantes que vous devrez prendre consiste à identifier l'objectif ciblé en développant un modèle d'interpolation. Autrement dit, vous devez savoir quelles informations vous attendez du modèle pour pouvoir prendre une décision. Par exemple, dans le domaine de la santé publique, les modèles d'interpolation permettent de prévoir les niveaux de contaminants pouvant être statistiquement associés à des taux de maladie. En fonction de ces informations, des études d'échantillonnage plus poussées peuvent être préparées, des politiques de santé publique peuvent être mises en place, etc.
Geostatistical Analyst propose une grande variété de méthodes d'interpolation. Chacune d'elle présente des avantages uniques et génère des informations différentes (dans certains cas, les méthodes fournissent des informations semblables, et dans d'autres, les informations peuvent être très différentes). Les diagrammes suivants illustrent ces méthodes classées selon divers critères. Choisissez un critère déterminant dans votre cas et une branche dans l'arborescence correspondante qui représente l'option choisie. Vous aurez ainsi le choix entre une ou plusieurs méthodes d'interpolation adaptées à votre situation. Il est très probable que vous deviez satisfaire à plusieurs critères et que vous utilisiez plusieurs arborescences de classification. Comparez les méthodes d'interpolation suggérées par chaque branche de l'arborescence et choisissez quelques méthodes à mettre en parallèle avant de choisir un modèle.
La première arborescence propose des méthodes en fonction de leur capacité à générer des prévisions ou des prévisions et les erreurs associées.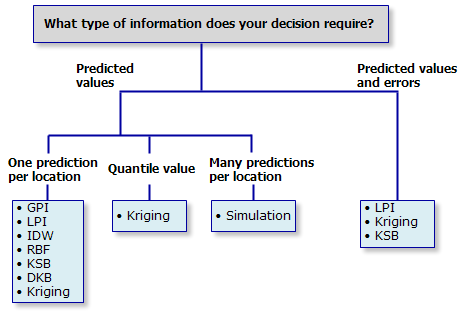
Certaines méthodes nécessitent un modèle d'auto-corrélation spatiale pour générer des valeurs prévues, mais ce n'est pas le cas pour toutes les méthodes. La modélisation de l'auto-corrélation spatiale implique la définition d'autres valeurs de paramètres et l'ajustement interactif d'un modèle aux données.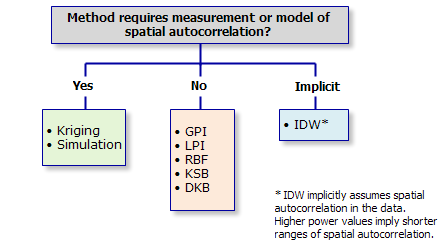
Chaque méthode génère un type différent de sortie. C'est pourquoi vous devez savoir quel type d'informations vous devez générer avant de créer le modèle d'interpolation. 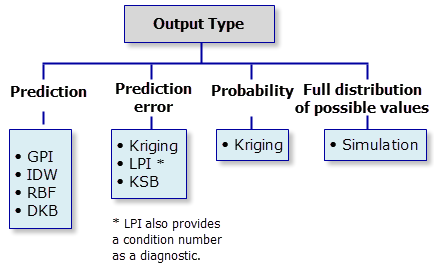
Les méthodes d'interpolation varient selon leur niveau de complexité qui peut être mesuré en fonction du nombre d'hypothèses devant être vérifiées pour que le modèle soit valide. 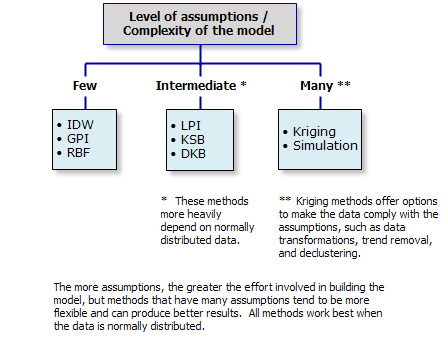
Certains interpolateurs sont exacts (à chaque emplacement des données en entrée, la surface aura exactement la même valeur que celle des données en entrée), alors que certains autres ne le sont pas. Dans certains cas, les données en entrée devront être exactement répliquées. 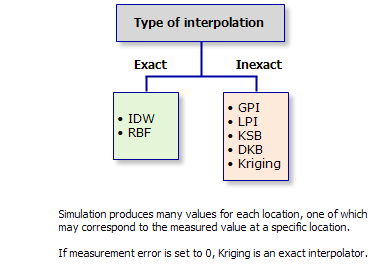
Certaines méthodes produisent des surfaces plus lisses que d'autres. Par exemple, les fonctions de base radiale sont lisses de par leur construction. Un voisinage de recherche lisse produira des surfaces plus lisses qu'un voisinage de recherche standard. 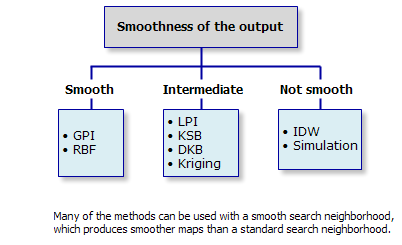
Pour certaines décisions, vous devez prendre en compte non seulement la valeur prévue à un emplacement, mais également l'incertitude (variabilité) de cette prévision. Certaines méthodes proposent des mesures de l'incertitude, alors que d'autres n'en proposent pas. 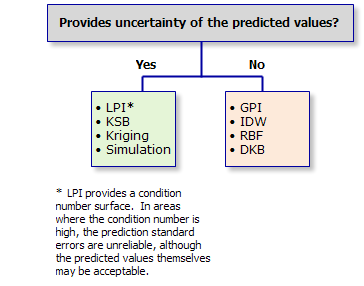
Pour finir, la vitesse de traitement peut être un facteur déterminant dans votre analyse. Habituellement, la plupart des méthodes d'interpolation sont assez rapides, sauf quand des interruptions sont utilisées pour contrôler le processus d'interpolation. 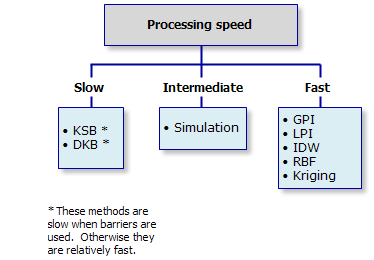
Les arborescences de classification utilisent les abréviations suivantes pour identifier les méthodes d'interpolation :
| Abréviation | Nom de la méthode |
|---|---|
GPI | |
LPI | |
IDW | |
RBF | |
KSB | |
DKB | |
Krigeage | Ordinaire, simple, universel, indicateur, probabilité, disjonctif et krigeage bayésien empirique |
Simulation | Simulation géostatistique gaussienne basée sur un modèle de krigeage simple |