Disponible avec une licence Geostatistical Analyst.
Les fonctions de base radiale (RBF) sont une série de techniques d'interpolation exacte qui impliquent le passage de la surface par chaque valeur d'échantillon mesuré. Il existe cinq fonctions de base différentes :
- Spline de plaque fine
- Spline avec tension
- Spline entièrement régularisée
- Fonction multiquadratrique
- Fonction multiquadratrique inverse
Chaque fonction de base présente une forme différente et produit une surface d'interpolation différente. Les méthodes RBF représentent un cas particulier de splines.
Le concept des fonctions de base radiale revient à l'ajustement d'une membrane en caoutchouc à travers les valeurs d'échantillons mesurés tout en réduisant au maximum la courbure totale de la surface. La fonction de base sélectionnée vous permet de déterminer comment la membrane en caoutchouc va être ajustée entre les valeurs. Le diagramme suivant explique en théorie comment une surface RBF est ajustée en passant par une série de valeurs d'échantillons d'altitude. Vous remarquerez que dans la section croisée, la surface passe par les valeurs de données.
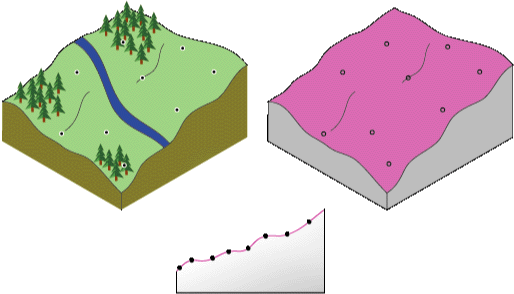
En tant qu'interpolateurs exacts, les méthodes RBF diffèrent des interpolateurs polynomiaux globaux et locaux qui sont tous deux inexacts et n'exigent pas que la surface passe par les points mesurés. Si l'on compare les méthodes RBF et IDW (également un interpolateur exact), la méthode IDW ne prévoit jamais de valeurs supérieures aux valeurs mesurées maximum ou inférieures aux valeurs mesurées minimum comme vous pouvez le constater dans la section croisée d'une coupe des échantillons de données ci-dessous.

Toutefois, les méthodes RBF peuvent prévoir des valeurs supérieures et inférieures aux valeurs mesurées maximum et minimum comme l'indique la section croisée ci-dessous.

Des paramètres optimaux sont déterminés à l'aide de la validation croisée, comme cela est expliqué pour la méthode IDW et l'interpolation polynomiale locale.
Quand utiliser des fonctions de base radiale
Les méthodes RBF permettent de produire des surfaces lisses à partir d'un grand nombre de points de données. Les fonctions produisent des résultats satisfaisants pour des surfaces aux variations subtiles, telle que l'altitude.
Toutefois, les techniques ne sont pas adaptées lorsque des valeurs de surface présentent des variations considérables sur des distances réduites et/ou lorsque vous pensez que les échantillons de données sont sujets à des erreurs de mesure ou incertains.
Concepts des fonctions de base radiale
Dans Geostatistical Analyst, les méthodes RBF sont formées à chaque emplacement de données. Une fonction RBF évolue en fonction de la distance par rapport à un emplacement.
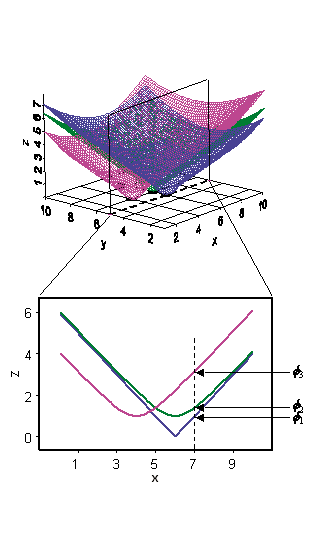
Supposez, par exemple, que la fonction de base radiale représente simplement la distance par rapport à chaque emplacement. Elle forme ainsi un cône inversé au-dessus de chaque emplacement. Si vous observez une section croisée du plan x,z et que y = 5, vous remarquerez une tranche de chaque fonction de base radiale. Supposons maintenant que vous prévoyiez une valeur si y = 5 et x = 7. La valeur de chaque fonction de base radiale à l'emplacement de prévision peut être extraite de la figure ci-dessus produite par les valeurs Φ1, Φ2 et Φ3 qui dépendent simplement de la distance par rapport à chaque emplacement de données. Le mesure de prévision résulte de la moyenne pondérée w1Φ1 + w2Φ2 + w3Φ3 + …
Il convient maintenant de déterminer les pondérations. Jusqu'à présent, vous n'avez pas utilisé les valeurs de données. Les pondérations w1, w2, w3, etc, sont déterminées à la condition que, lorsqu'une prévision est transférée vers un emplacement présentant une valeur mesurée, la prévision de la valeur de données est exacte. Il en résulte N équations avec N inconnues qui peuvent être résolues de manière unique. De cette façon, la surface passe par les valeurs de données, garantissant ainsi l'exactitude des prévisions.
Dans cet exemple, la fonction de base radiale est un cas particulier de fonction RBF multiquadratique. Geostatistical Analyst vous permet également d'utiliser d'autres méthodes RBF, telles que des splines entièrement régularisées, des splines de plaque fine, des splines avec tension, et des fonctions multiquadratiques inverses. Parfois la différence entre ces fonctions n'est pas considérable, mais vous pouvez choisir celle qui vous convient ou en essayer plusieurs et faire appel à la validation croisée pour en sélectionner une. Chacune des méthodes RFB comporte un paramètre qui contrôle le lissage de la surface.

Pour toutes les méthodes, à l'exception de la fonction multiquadratique inverse, plus la valeur du paramètre est élevée, plus la carte est lisse. Pour la fonction multiquadratique inverse, c'est l'inverse qui se produit.