Mit der Geostatistical Analyst-Lizenz verfügbar.
Radiale Basisfunktionen (RBFs) sind eine Reihe von exakten Interpolationsmethoden, d. h., die Oberfläche muss durch jeden gemessenen Referenzpunkt verlaufen. Fünf unterschiedliche Basisfunktionen sind vorhanden:
- Thin-Plate Spline
- Spline mit Tension
- Spline mit vollständiger Regelung
- Funktion "Multiquadric"
- Funktion "Inverse Multiquadric"
Jede Basisfunktion hat ein anderes Shape und ergibt eine andere Interpolationsoberfläche. RBF-Methoden stellen einen Sonderfall von Splines dar.
RBFs sind konzeptuell ähnlich wie das Einpassen einer Gummimembran auf die gemessenen Referenzpunkte bei gleichzeitiger Minimierung der Gesamtkrümmung der Oberfläche. Die ausgewählte Basisfunktion bestimmt, wie die Gummimembran zwischen den Werten verläuft. Das folgende Diagramm illustriert, wie eine RBF-Oberfläche durch eine Reihe von Höhenreferenzwerten verläuft. Beachten Sie, dass die Oberfläche im Querschnitt durch die Datenwerte verläuft.
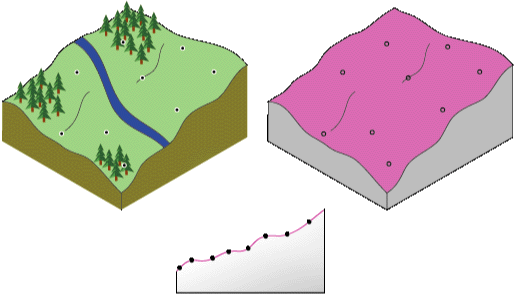
Da RBF-Methoden genaue Interpolatoren sind, unterscheiden sie sich von globalen und lokalen polynomialen Interpolatoren, die ungenaue Interpolatoren sind und nicht erfordern, dass die Oberfläche durch die gemessenen Punkte verläuft. IDW (ebenfalls ein genauer Interpolator) sagt im Vergleich zu RBF nie Werte oberhalb des höchsten oder unterhalb des niedrigsten gemessenen Werts vorher, wie im folgenden Querschnitt eines Transekts von Referenzdaten gezeigt.

Die RBFs können jedoch Werte oberhalb des höchsten und unterhalb des niedrigsten gemessenen Wertes vorhersagen, wie im nachfolgenden Querschnitt gezeigt.

Optimale Parameter werden mithilfe von Kreuzvalidierung auf ähnliche Weise bestimmt, wie für IDW und lokale polynomiale Interpolation erläutert.
Einsatzmöglichkeiten von radialen Basisfunktionen
RBFs werden verwendet, um aus einer großen Anzahl von Datenpunkten glatte Oberflächen zu erzeugen. Die Funktionen liefern gute Ergebnisse für leicht variierende Oberflächen wie Höhenoberflächen.
Die Methoden sind jedoch ungeeignet, wenn in den Oberflächenwerten große Veränderungen in kurzen Abständen auftreten und/oder wenn Sie vermuten, dass die Referenzdaten anfällig für Messfehler oder mit Unsicherheiten behaftet sind.
Grundlegende Konzepte der radialen Basisfunktionen
In Geostatistical Analyst werden RBFs über jeder Datenposition gebildet. Eine RBF ist eine Funktion, die sich mit dem Abstand von einer Position ändert.
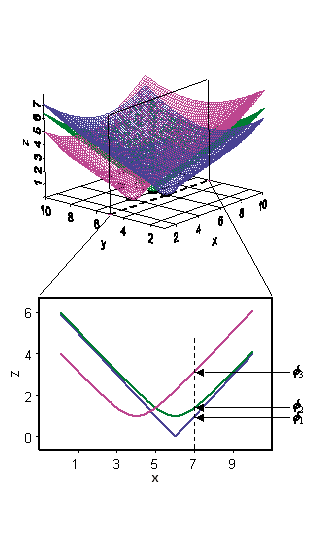
Nehmen Sie beispielsweise an, die radiale Basisfunktion sei einfach die Entfernung von jeder Position und bilde einen umgekehrten Kegel über jeder Position. Wenn Sie einen Querschnitt der XZ-Ebene für y = 5 nehmen, sehen Sie eine Scheibe jeder radialen Basisfunktion. Nehmen Sie nun an, Sie möchten einen Wert bei y = 5 und x = 7 vorhersagen. Der Wert jeder radialen Basisfunktion an der Vorhersageposition lässt sich der obigen Abbildung entnehmen, gegeben von den Werten Φ1, Φ2 und Φ3, die einfach von der Entfernung von jeder Datenposition abhängen. Die Vorhersage erfolgt durch Ermittlung des gewichteten Durchschnitts w1Φ1 + w2Φ2 + w3Φ3 + …
Nun stellt sich die Frage, wie die Gewichtungen zu bestimmen sind. Bisher haben Sie die Datenwerte noch gar nicht verwendet. Die Gewichtungen w1, w2, w3 usw. ergeben sich dadurch, dass bei Verschieben der Vorhersage an eine Position mit einem gemessenen Wert die genaue Vorhersage des Datenwerts erforderlich ist. Damit werden N Gleichungen mit N Unbekannten gebildet, die eindeutig gelöst werden können. Daher verläuft die Oberfläche durch die Datenwerte und sorgt für genaue Vorhersagen.
Die radiale Basisfunktion in diesem Beispiel ist ein Sonderfall der RBF "Multiquadric". Mit Geostatistical Analyst können Sie auch andere RBFs verwenden, z. B. "Spline mit vollständiger Regelung", "Thin-Plate Spline", "Spline mit Tension" und "Inverse Multiquadric. Manchmal ist der Unterschied zwischen diesen nicht groß, aber Sie haben möglicherweise einen Grund dafür, eine bestimmte Funktion auszuwählen. Sie können auch mehrere ausprobieren und eine davon mithilfe von Kreuzvalidierung auswählen. Jede der RBFs verfügt über einen Parameter, der die Glattheit der Oberfläche steuert.

Für alle Methoden mit Ausnahme von "Inverse Multiquadric" gilt: Je höher der Parameterwert, umso glatter ist die Karte. Für "Inverse Multiquadric" trifft das Gegenteil zu.