Die Kernel-Interpolation ist eine Variante einer lokalen Polynominterpolation erster Ordnung, bei der die Instabilität bei Berechnungen mit einer Methode verhindert wird, die der bei der Ridge Regression verwendeten Methode zum Schätzen der Regressionskoeffizienten ähnelt. Wenn die Schätzung nur eine leichte Verzerrung aufweist und sie viel genauer ist als eine erwartungstreue Schätzfunktion, kann es durchaus die bevorzugte Schätzung sein. Details zu Ridge Regression finden Sie beispielsweise in Hoerl and Kennard (1970).
Vorhersagefehler bei der lokalen Polynominterpolation werden unter der Voraussetzung geschätzt, dass die räumliche Bedingungsnummer überall sehr klein ist. Diese Voraussetzung wird häufig verletzt und die räumliche Bedingungsnummer hebt Bereiche hervor, in denen Vorhersagen und standardmäßige Vorhersagefehler instabil sind. Beim Modell der Kernel-Glättung wird das Problem übermäßiger Fehler der standardmäßigen Vorhersage mithilfe des Ridge-Parameters korrigiert, indem eine geringfügige Verzerrung bei den Gleichungen eingesetzt wird. Dadurch wird die Karte der räumlichen Bedingungsnummer überflüssig. Daher bietet die Kernel-Interpolation für den Ausgabe-Oberflächentyp nur Vorhersagen und standardmäßige Vorhersagefehler. Da der Ridge-Parameter Verzerrungen einsetzt, um die Vorhersagen zu stabilisieren, sollte er so klein wie möglich sein und dabei die Modellstabilität aufrechterhalten. Details zu diesem Prozess finden Sie in "Local Polynomials for Data Detrending and Interpolation in the Presence of Barriers", Gribov and Krivoruchko (2010).
Ein weiterer Unterschied zwischen den beiden Modellen ist, dass das Modell der Kernel-Interpolation die kürzeste Entfernung zwischen Punkten verwendet, sodass Punkte an den Seiten der angegebenen nicht transparenten (absoluten) Barriere mit einer Reihe von geraden Linien verbunden sind.
Die Kernel-Interpolation verwendet die folgenden radial-symmetrischen Kernels: Exponential, Gauß'sche, Quartic, Biquadratisch, Epanechnikov, Polynom 5. Ordnung und Konstant. Die Bandbreite des Kernels wird durch ein Rechteck um die Beobachtungen bestimmt.
Der Epanechnikov-Kernel liefert in der Regel bessere Ergebnisse, wenn Polynome erster Ordnung verwendet werden. Je nach Daten können die Kreuzvalidierungs- und Validierungsdiagnosen jedoch einen anderen Kernel vorschlagen, Fan and Gijbels (1996).
Nachfolgend werden die Vorhersagen der Kernel-Interpolation mit Barrieren, links, und ohne Barrieren, rechts, miteinander verglichen. Beachten Sie, wie sich die Konturlinien in der Grafik links abrupt an den Barrieren ändern, die Konturlinien in der Grafik rechts jedoch glatt über die Barrieren verlaufen.
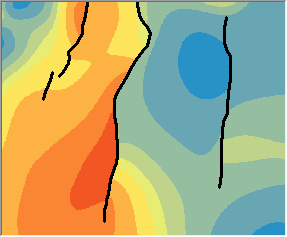
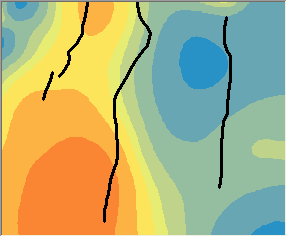
Modelle, die auf der kürzesten Entfernung zwischen Punkten basieren, sind möglicherweise in hydrologischen und meteorologischen Anwendungen vorzuziehen.
Kernel-Funktionen
Kernel-Funktionen: bei allen nachfolgenden Formeln ist r der am Punkt s zentrierte Radius und h die Bandbreite.
- Exponential:
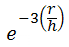
- Gauß'sche:
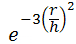
- Biquadratisch:
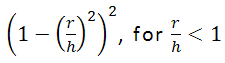
- Epanechnikov:
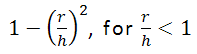
- PolynomialOrder5:
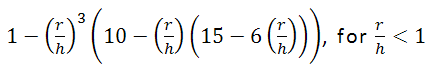
- Konstant:
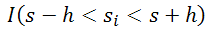
wobei I(Ausdruck) eine Indikatorfunktion ist, die den Wert 1 verwendet, wenn der Ausdruck "true" (wahr) ist, und den Wert 0, wenn der Ausdruck "false" (falsch) ist.
Der Bandbreitenparameter gilt für alle Kernel-Funktionen, mit Ausnahme von "Konstant". Die Kernel-Funktionen Exponential, Gauß'sche und Konstant unterstützen zusätzlich Smooth Searching Neighborhood, um den Kernel-Bereich zu begrenzen.
Literaturhinweise
Fan, J. and Gijbels, I. (1996). Local Polynomial Modelling and Its Applications, Chapman & Hall. London.
Hoerl, A.E. and Kennard, R.W. (1970), Ridge regression: biased estimation for nonorthogonal problems, Technometrics, 12, 55-67.
Yan, Xin. (2009) Linear regression analysis : theory and computing. Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224.