Доступно с лицензией Geostatistical Analyst.
Концепции имитации
Имитация в широком понимании определена как процесс репликации реальности с помощью модели. В геостатистике имитация – это реализация случайной функции (поверхности) с теми же статистическими характеристиками, что и опорные данные, используемые для ее генерации (средним значением, дисперсией и вариограммой). Конкретнее, геостатистическое моделирование Гаусса (GGS) используется для непрерывных данных и предполагает, что данные и преобразование данных имеют нормальное распределение Гаусса. Основное предположение GGS заключается в том, что данные являются стационарными, то есть среднее значение, дисперсия и пространственная структура (вариограмма) не меняются в пространственной области данных. Другое основное предположение GGS заключаются в том, что случайная моделируемая функция является многомерной случайной функцией Гаусса.
GGS имеет преимущество над кригингом. Так как кригинг основан на локальном среднем данных, он выдает сглаженные выходные данные. С другой стороны, GGS выдает лучшее представление локальной изменчивости, поскольку включает локальную вариабельность, которую упускает кригинг, в генерируемые поверхности. Вариабельность, которую реализации GGS включают в интерполируемое значение в конкретном местоположении, имеет нулевую среднюю точку, так что среднее множества реализаций GGS проявляет тенденцию к интерполяции кригинга. Данная концепция представлена на рисунке ниже. Различные реализации представлены как стек выходных слоев, а распределение значений в конкретной координате является Гауссовским со средним значением, равным кригинговой оценке для этого местоположения, и разбросом, определенным дисперсией кригинга в данном местоположении.
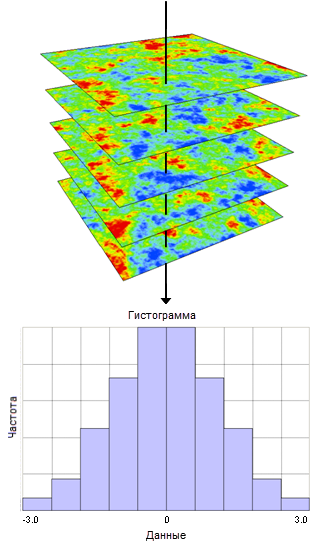
Инструмент Extract Values To Table (Извлечь значения в таблицу) используется для получения данных для диаграммы, представленной на рисунке ниже, а также содействует в последующей обработке выходных данных, генерируемых GGS.
Возрастающее использование GGS следует за тенденцией в геостатистической практике, которая акцентирует внимание на характеристике неопределенности для принятия решений и анализа риска, вместо выполнения лучшей несмещнной интерполяции для каждого неопорного местоположения (как это делает кригинг), которое больше подходит для демонстрации глобальных трендов в данных (Deutsch and Journel 1998, Goovaerts 1997). Имитация также преодолевает проблему условного смещения в кригинговых оценках (области с высоким значением обычно выдают заниженные прогнозы, тогда как области с низким значением, как правило, выдают завышенные прогнозы).
Геостатистическое моделирование создает несколько равновероятных представлений пространственного распределения исследуемого атрибута. Данные представления дают возможность измерять неопределенность для всех неопорных местоположений, взятых вместе в пространстве, а не по одному (как измеряется кригинговой дисперсией). Более того, кригинговая дисперсия обычно не зависит от значений данных и не может использоваться как мера точности оценки. С другой стороны, точность оценки может измеряться с помощью построения распределений оценочных значений для неопорных местоположений, использующих несколько смоделированных реализаций, которые построены из модели простого кригинга при использовании входных, нормально распределенных данных (то есть данных, которые нормально распределены либо преобразованы по методу нормальных меток или другого типа преобразования). Данные распределения неопределенности являются ключевыми для оценки рисков и анализа решения, использующих значения оценочных данных.
GGS предполагает, что данные нормально распределены, что редко встречается на практике. К данным применяется преобразование по методу нормальных меток, так что данные подчиняются стандартному нормальному распределению (среднее = 0 и дисперсия = 1). Затем для таких нормально распределенных данных выполняется имитация, а результаты преобразовываются обратно для получения смоделированных выходных данных в исходных единицах. При выполнении простого кригинга на нормально распределенных данных выполняется оценка кригинга и дисперсия, которые полностью определяют условное распределение в каждом местоположении исследуемой области. Это позволяет отобразить смоделированные реализации случайной функции (неизвестные эталонные поверхности), зная только два этих параметра в каждом местоположении, и является причиной того, что метод GGS основан на модели простого кригинга и нормально распределенных данных.
Инструмент геостатистического моделирования Гаусса позволяет выполнять два типа имитаций:
- Условная имитация учитывает значения данных (если только погрешность измерения не была включена в модель кригинга). Некоторые различия между измеренными и смоделированными значениями для опорных местоположений могут возникнуть из-за того, что модель генерирует значения в центрах ячеек сетки, которые не в точности соответствуют положению опорных точек. Также условная имитация реплицирует среднее, дисперсию и вариограмму данных в среднем, то есть усредненные по множеству реализаций. Смоделированные поверхности выглядят как карты проинтерполированных значений кригинга, но демонстрируют большую пространственную вариабельность.
- Абсолютная имитация не учитывает значения данных, но реплицирует среднее, дисперсию и вариограмму данных (в среднем). Смоделированные поверхности демонстрируют пространственную структуру, подобную карте кригинга, но области высоких и низких значений не обязательно возникают там, где присутствуют высокие и низкие значения во входных данных.
Примеры имитаций
Пример 1
Качество атмосферы является важным для здоровья фактором во многих городах и по всему миру. В США Лос-Анджелес известен низким качеством атмосферы. Ежедневно крупная сеть мониторинга собирает данные по концентрации озона и твердых частиц в воздухе, а также другим загрязнениям. Данные о качестве атмосферы сообщаются в виде концентрации для каждого загрязнителя, а также выдается количество дней в году, когда загрязнение превышало стандарты качества атмосферы по штату и по стране (http://www.arb.ca.gov/html/ds.htm). Тогда как оба измерения позволяют частично оценить риск для жизни в конкретных областях, количество дней в году, когда были превышены критические пороги загрязнения, могут использоваться для создания карт интерполяций, демонстрирующих вероятности превышения порога.
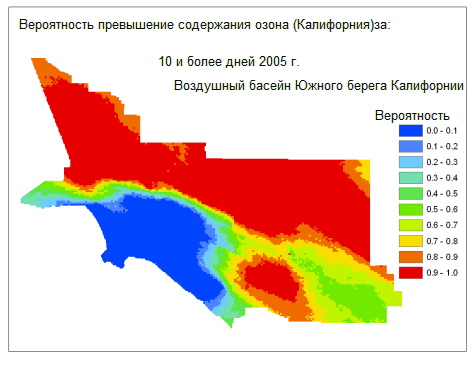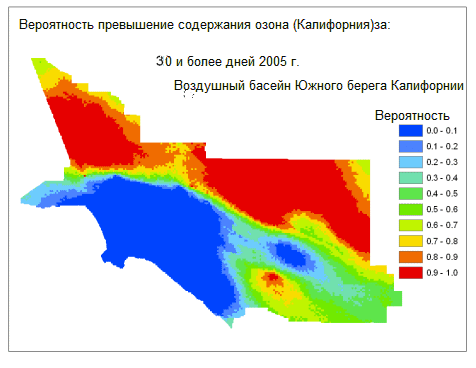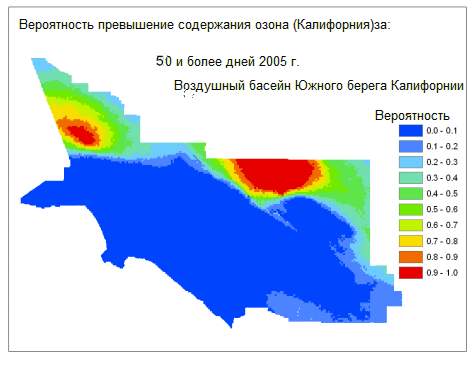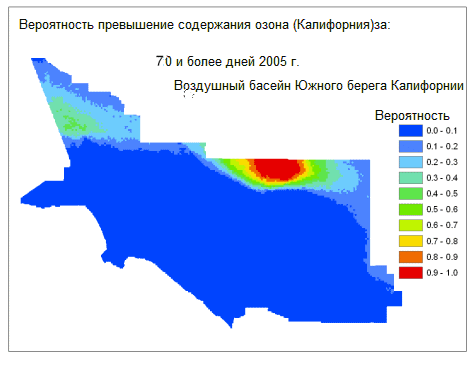
В данном примере в течение 2005 года на каждой станции мониторинга наблюдалось количество дней, в которых был превышен порог концентрации озона в штате Калифорния, и созданы вариограммы. Для создания нескольких реализаций использовалась условная имитация. Каждая реализация – это карта с количеством дней, в которых были превышены пороговые значения загрязнения в течение 2005 года. Затем реализации обработали повторно для оценки вероятностей превышения порога загрязнения в штате более 10, 20, 30, 40, 50, 60 и 70 дней в году (каждой станцией было зарегистрировано не более 80 дней, когда был превышен порог загрязнения). На рисунке внизу представлены карты результатов для концентрации озона в воздушном бассейне Южного побережья, в которое входит Лос-Анджелес и континентальные города. Качество атмосферы вблизи побережья гораздо лучше, чем в областях внутренней части страны, в основном из-за ветров, преимущественно западно-восточных в этом регионе.
Такие карты полезны при определении приоритетов в стратегии борьбы с загрязнением, для установления взаимосвязи между здоровьем и качеством окружающей среды и для населения при принятии решения о месте жительства. Карты предоставляют сведения, которые помогают отвечать на такие вопросы: «Какое количество загрязнений я готов вытерпеть?» и «Сколько загрязнений присутствует в конкретной области, в которой я собираюсь жить?»
Пример 2
Существует множество приложений, в которых используются пространственно зависимые переменные в качестве входных данных для моделей (например, имитация течения в технологии нефти). В таких случаях неопределенности в результатах модели оцениваются путем создания ряда имитаций с помощью следующих процедур:
- 1. Для переменной моделируется большое количество равновероятных реализаций.
- 2. Модель (обычно называемая функцией преобразования) выполняется при использовании смоделированной переменной в качестве входных данных.
- 3. Резюмируются запуски модели для оценки изменчивости в выходных данных модели.
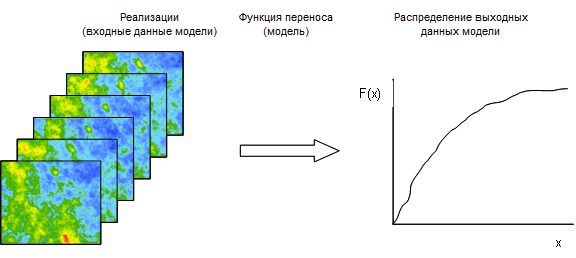
Статистика выходных данных измеряет неопределенность модели.
Примером процедуры, описанной выше, в реальном мире является исследование, проведенное для опытной установки для изоляции отходов в WIPP в юго-восточной части Нью-Мексико в качестве объекта хранения трансурановых радиоактивных отходов (http://www.wipp.energy.gov/).
Ученые определили солевые отложения, которые находятся на глубине более 610 м под поверхностью земли, как потенциальный объект хранения для отходов производства. Но только отложения, находящиеся выше водоносного пласта. Имелись опасения, что подземные воды будут переносить отходы, которые могут просачиваться с участка. Для того чтобы продемонстрировать безопасность WIPP, ученым необходимо было убедить Агентство охраны окружающей среды США в том, что скорость грунтовой воды, протекающей через водоносный пласт, достаточна мала, так что загрязнение окружающей среды крайне маловероятно.
Значения проницаемости определяют скорость потока воды через водоносный пласт, и несколько таких значений были получены для водоносного пласта возле предлагаемого участка WIPP. Грунтовые воды смоделированы с помощью уравнений водного баланса, которые решаются численно и которым необходимы значения проницаемости, проинтерполированные по регулярной сетке. При использовании кригинговых оценок проницаемости значения проницаемости должны основываться на (взвешенных) средних значениях проницаемости окрестностей, а моделируемое время движения грунтовых вод должно основываться на этих средних значениях. Поскольку кригинг создает сглаженные карты, области чрезвычайно высоких и низких значений проницаемости не попадут в интерполированные поверхности. Для точного анализа рисков ученые должны были рассмотреть наихудший из возможных вариантов и таким образом произвести полное распределение вероятности значений времени пути. При этом для оценки стабильности WIPP ученые могли использовать более низкие значения хвоста распределений времени пути грунтовых вод (в соответствии с чрезвычайно высокой скоростью потока), а не среднее время пути. Условное моделирование использовалось для выполнения распределений вероятностей значений времени пути.
Возможность переноса продуктов отходов грунтовыми водами была одним из множества вариантов риска для здоровья людей, рассмотренных в оценке стабильности WIPP. Комплексный анализ рисков играет большую роль в оценке WIPP для захоронения радиоактивных отходов и убеждении общественности и государственных чиновников в приемлемости опытной установки для изоляции отходов. После более 20 лет научных исследований, общественных опросов и нормативной борьбы 26 марта 1999 года началось строительство опытной установки для изоляции отходов (WIPP).
Сколько реализаций необходимо сгенерировать?
Результаты изучения путем моделирования не должны зависеть от количества сгенерированных реализаций. Одним из способов определения количества генерируемых реализаций является сравнение статистических величин для различного числа реализаций в небольшой части области данных (для экономии времени используется поднабор данных). Статистические величины проявляют тенденцию к постоянным величинам по мере увеличения количества реализаций. Статистические величины, исследуемые в примере ниже, являются первыми и третьими квартилями, рассчитанными для маленького участка (поднабор) смоделированных поверхностей высот (в футах над уровнем моря) для штата Висконсин, США.
На верхней диаграмме показаны колебания высоты для первых 100 реализаций. На нижней диаграмме представлены результаты 1000 реализаций.
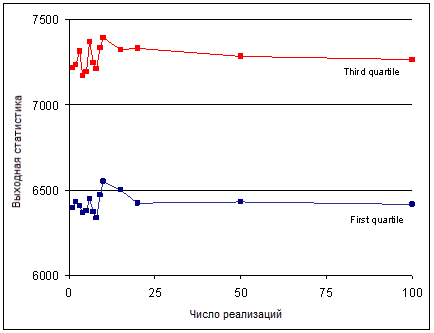
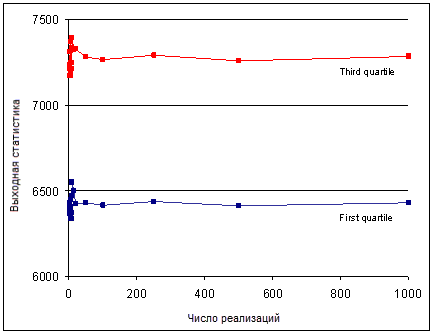
В данном случае значения стабилизируются после 20 имитаций. Во многих случаях по меньшей мере 100 реализаций предоставляют достаточно информации для определения среднего и вероятностей превышения пороговых значений. Большее количество реализаций дает более высокую степень достоверности сводных данных и выходных переменных модели, но требуют большего времени для проведения расчетов.
Более подробно о том, как геостатистическое моделирование Гаусса реализуется в ArcGIS, см. в разделе How Gaussian Geostatistical Simulations work (Как работает геостатистическое моделирование Гаусса).
Ссылки
Deutsch, C.V., and A. G. Journel. 1998. GSLIB Geostatistical Software Library and User's Guide. 2nd Ed. Oxford University Press, New York, pages 119–122.
Goovaerts, P. 1997. Geostatistics for Natural Resource Evaluation. Oxford University Press, New York, pages 369–376.