Нечеткое множество—Справка

Доступно с лицензией Spatial Analyst.

Краткая информация
Использование
Синтаксис
Пример кода
Параметры среды
Информация о лицензировании

Краткая информация

Трансформирует входной растр по шкале от 0 до 1, указывая полноту принадлежности в наборе на основе заданного алгоритма подготовки задачи для решения методами нечеткой логики.

Значение 1 означает полную принадлежность к нечеткому множеству, с уменьшающейся принадлежностью до 0, что указывает на то, что значение не принадлежит к нечеткому множеству.

Более подробно о том, как работает инструмент Нечеткое множество

Использование

Этот инструмент не трансформирует категорийные данные. Чтобы включить категорийные данные в анализ нечеткого наложения, необходима предварительная обработка ячеек. Вы можете создать модель или запустить следующие инструменты геообработки. Сначала используйте инструмент Переклассификация, чтобы предоставить новый диапазон значений (например, 1 к 100). Затем разделите результат на коэффициент (например, на 100), чтобы нормализовать выходные значения от 0,0 до 1,0.
Распределение показывает, как быстро значения принадлежности к нечёткому множеству уменьшаются от 1 до 0. Чем больше значение, тем резче изменение вокруг центральной точки. Говоря другими словами, при уменьшении значения распределения, значения принадлежности к нечеткому достигают 0 медленнее. Выборка соответствующего значения распределения – это субъективный процесс, который зависит от диапазона четких значений. Для опции Гауссова или Ближайший можно начать со значения по умолчанию, равного 0,1. Как правило, значения варьируются в диапазоне [0,01–1] или [0,001-1], соответственно. Для опций Маленькие и Большие, можно начать со значения по умолчанию, равного 5, и значения, как правило, варьируются от 1 до 10.
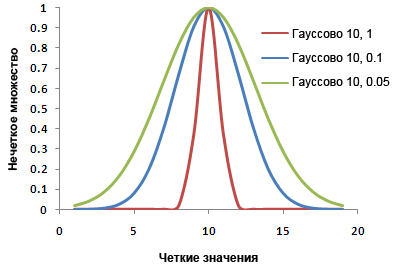
Влияние на распределение на Гауссовом нечетком множестве.
Это может быть тем случаем, когда ни у одного входного значения не будет 100 процентной возможности быть членом указанного набора. Другими словами, ни у одного значения нет нечеткого множества 1. В этой ситуации, возможно, вы захотите сдвинуть значения нечеткого множества для отражения новой шкалы. Например, если наибольшее значение принадлежности для входных значений – 0,75, то вы можете установить новую шкалу, умножая каждое нечеткое множество на 0,75.
Применяемые ограничения: VERY и SOMEWHAT. VERY также называется концентрацией и определяется как функция нечеткого множества в квадрате. SOMEWHAT также называется растяжением или «Больше или Меньше». Это квадратный корень функции нечеткого множества. Ограничения VERY и SOMEWHAT увеличивают и уменьшают функции нечеткого множества соответственно.
Отрицательные значения неприемлемы для функций нечеткого множества Маленький и Большой.
Для функции нечеткого множества Линейный входной растр должен быть упорядоченными данными. Минимум может быть меньше максимума для создания положительного уклона, или больше максимума для создания отрицательного уклона для трансформации.
Если минимум меньше максимума, для трансформации используется функция с положительным уклоном; если минимум больше максимума, используется функция с отрицательным уклоном.
См. раздел Среда анализа и Spatial Analyst для получения дополнительной информации о среде геообработки данного инструмента.

Синтаксис

FuzzyMembership (in_raster, {fuzzy_function}, {hedge})

Параметр	Объяснение	Тип данных
in_raster	Входной растр, значения которого будут переклассифицированы по шкале от 0 до 1.	Raster Layer
fuzzy_function (дополнительно)	Задает алгоритм, используемый в подготовке задачи для решения методами нечеткой логики для входного растра. Нечеткие классы используются для определения типа принадлежности. Типы классов принадлежности: FuzzyGaussian, FuzzyLarge, FuzzyLinear, FuzzyMSLarge, FuzzyMSSmall, FuzzyNear, and FuzzySmall. Формы классов принадлежности: FuzzyGaussian({midpoint},{spread}) FuzzyLarge({midpoint},{spread}) FuzzyLinear({minimum},{maximum}) FuzzyMSLarge({meanMultiplier},{STDMultiplier}) FuzzyMSSmall({meanMultiplier},{STDMultiplier}) FuzzyNear({midpoint},{spread}) FuzzySmall({midpoint},{spread})	Fuzzy function
hedge (дополнительно)	Задание ограничений увеличивает или уменьшает значения принадлежности, которые изменяют значения нечеткого множества. Применяемые защиты используются для того, чтобы оказать помощь в управлении критериями или важными атрибутами. NONE —Ограничения не применяются. Это значение используется по умолчанию. SOMEWHAT —Растяжение определяется как квадратный корень функции нечеткого множества Это ограничение увеличивает функции нечеткого множества. VERY —Также известен как концентрация, определенная как функция нечеткого множества в квадрате. Это ограничение уменьшает функции нечеткого множества.	String

Возвращено значение

Имя	Объяснение	Тип данных
out_raster	Выходными данными будет растр со значениями с плавающей точкой в диапазоне от 0 до 1.	Raster

Пример кода

FuzzyMembership, пример 1 (окно Python)

Этот пример создает растр принадлежности, с помощью функцию Гауссова, где у значений высот близких к средней точке (1,200 футов) выше значения принадлежности.

import arcpy
from arcpy.sa import *
from arcpy import env
env.workspace = "c:/sapyexamples/data"
outFzyMember = FuzzyMembership("elevation", FuzzyGaussian(1200, 0.06))
outFzyMember.save("c:/sapyexamples/fzymemb")

FuzzyMembership, пример 2 (автономный скрипт)

В этом примере создается растр нечеткого множества, с помощью функции Гаусса (Gaussian), где у значений высот близких к средней точке (1,200 футов) значения принадлежности выше.

# Name: FuzzyMembership_Ex_02.py
# Description: Scales input raster data into values ranging from zero to one
#     indicating the strength of a membership in a set. 
# Requirements: Spatial Analyst Extension

# Import system modules
import arcpy
from arcpy import env
from arcpy.sa import *

# Set environment settings
env.workspace = "C:/sapyexamples/data"

# Set local variables
inRaster = "elevation"

# Create the FuzzyGaussian algorithm object
midpoint = 1000
spread = 0.4
myFuzzyAlgorithm = FuzzyGaussian(midpoint, spread)

# Check out the ArcGIS Spatial Analyst extension license
arcpy.CheckOutExtension("Spatial")

# Execute FuzzyMembership
outFuzzyMember = FuzzyMembership(inRaster, myFuzzyAlgorithm)

# Save the output
outFuzzyMember.save("c:/sapyexamples/fzymemb2")

Параметры среды

Связанные темы

Отзыв по этому разделу?