
An analyst at a small and once-profitable political consulting firm has been poring through reams of data and analysis from the 2016 presidential election. The firm needs some exclusive information they can offer to clients so they can turn their fortunes around. While the demand for consulting services has exploded, so has the competition.
Having perused papers and articles from the primaries, the general election, and the aftermath, the analyst is well aware that a lot has been written on who, exactly, voted for Donald Trump. There is a general consensus that across the country his support came mainly from an older, whiter, and more working-class population. An article in The Atlantic from early in the primaries, for example, focused on blue-collar support for Trump.
But there are also articles, including one in The Washington Post from after the general election, that make a counterargument. The analyst thinks it would be really useful to try to pin down which demographic groups and other factors were key to Trump's success.
Regional variations
One election analysis the analyst read, from RealClearPolitics, addressed something she has been wondering about herself—did the vote for Trump vary across the country, among the various demographic groups? Was his support among blue-collar workers stronger in one region than another? What about his lack of support among people with a college degree?
She thinks that if she can show where these variations occur, future campaigns would be able to more effectively tailor their message to specific areas. With the right messaging, voters in these areas could perhaps be persuaded one way or the other. Or at least that's what the political parties believe, and as long as they believe it, they will make willing clients. (As a political analyst, she is a cynic by definition.)
A vast amount of money is spent on broad messaging platforms—television, radio, print—going to both national and local media outlets. On top of that, microtargeting voters via social media, by geographic location, is on the rise. Developing the right message for a specific demographic in a specific location is critical.
The analyst sees a lot of potential to provide analysis and consulting services to local and statewide campaigns in 2018. Beyond that, it looks like there will be a plethora of candidates in the 2020 Democratic primary, and possibly a number of challengers on the Republican side as well. If she can develop a methodology and produce useful information for the 2018 elections, there may be many potential clients in 2020, at both the local and national levels.
She pitches a demonstration project to the firm's principals. The idea is to develop a limited analysis—create just enough in the way of unique, actionable information to generate some attention and get clients interested in what the firm has to offer.
The firm's principals are intrigued, but resources are limited. They earmark a small amount for the project out of next quarter's research and marketing budgets.
She has approval for the project, but now she needs to produce results. How should she approach the task? Her ultimate goal is to look not only at correlations (like everyone else has done), but also at spatial variations in those correlations. The spatial analytics tools in ArcGIS should provide everything she needs.
Understanding broad spatial patterns
She begins by identifying the socioeconomic variables that best explain the 2016 election outcome. She will use regression analysis, specifically Exploratory Regression, to examine correlations. She can test, for example, how consistently the percentage of blue-collar workers or rates of unemployment in an area explain the percentage of people who voted for Trump in the general election nationwide.
While many of the analyses she's seen look at the vote on a state-by-state basis, to dig deeper she decides she will need to analyze the vote at the county level, as a few of the more detailed analyses have done. In short order, she downloads a United States county layer from the Living Atlas.
The variable she's trying to explain is the vote for Trump. In regression this is called the dependent variable. Since counties vary widely in population (and votes cast), she will use the percentage of votes for Trump in each county. After some searching online, she finally finds a reliable source for the vote by county. And it already includes the percentages, as well as the raw vote totals.

Now she needs the explanatory variables. For this analysis, she includes the variables that appeared most frequently in the literature—income, education level, race, age, and so on. The counties layer actually includes a few of these variables, but newer data is available. She will need the demographic data for 2016. Many of these are available via the ArcGIS Enrich Layer tool.
Again, she uses the percentage of the population in each category rather than the count. Using counts will merely show where the most people live—she wants to find out where a higher percentage of a particular demographic group in a county was associated with a higher vote for or against Trump, and where those relationships were significant. Her future clients will use that information to craft messages designed to encourage increased voting for their party by particular demographic groups.
In many cases, she has to calculate the percentages (for example, by dividing the number of Hispanics in each county by the total population of each). In other cases, she has to sum variables, and then calculate the percentage. For example, to find the percentage of people with a college degree in each county, she has to sum those with either a bachelor's degree or a graduate or professional degree, and then divide by the sum of adults in all education categories.

Finally, she has all the basic demographic variables—there are almost 30.
She decides to go ahead and run the analysis. Exploratory Regression creates models by combining explanatory variables. It identifies which combination—or model—does the best job of accounting for the dependent variable (the vote for Trump, in this case). For now, the analyst is less concerned with creating a viable model than with identifying the variables that consistently predict the election results. She runs Exploratory Regression specifying that it create models composed of combinations of three variables.
The report created by Exploratory Regression lists the most consistent variable relationships.
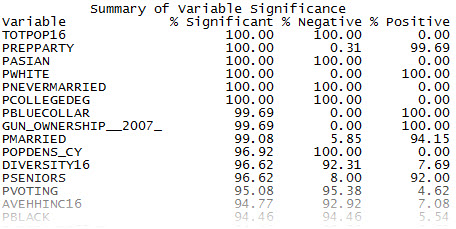
The % Significant column states how many times—when that variable was included in a model—it was statistically significant (100 percent is best). The % Negative and % Positive columns indicate how often the variable had a positive or negative relationship to the Trump vote. For a positive relationship, as the value of the variable increases, the Trump vote increases. For a negative relationship, as the value of the variable increases, the Trump vote decreases. Again, 100 percent for either positive or negative is most conclusive.
The analyst sees some interesting results in the list. The whiter the county, the higher the vote for Trump. That fits with the analyses she's seen. The percent Asian population has a negative relationship with the Trump vote. For some reason, counties with relatively larger percentages of Asians went strongly against Trump (or heavily for Hillary Clinton). Not much has been written about this, from what the analyst has read. Perhaps it's because the Asian population is a relatively small portion of the total. Still, in certain areas, this might be an important factor.
The percentage of singles (never married) and those with a college degree also have a negative relationship with the Trump vote. That also comports with much of the analysis she has seen.
The percentage of blue-collar workers shows up as significant, with a positive relationship with the Trump vote. This seems to support the argument of those who think the working-class vote was indeed a key factor in Trump's election.
Applying the science of where
The list of significant variables hints at which issues, and voting groups, future campaigns will want to try to address with specific messaging. But while knowing that Trump appealed to blue-collar voters is interesting, knowing in which regions he most effectively appealed to blue-collar workers will give the firm's clients the advantage they are looking for. It will allow them to focus their messaging on parts of the country where the relationship between the Trump vote and a particular group is strong.
Having identified the key factors, the analyst takes the next step and runs Geographically Weighted Regression (GWR) to find out where each variable has the strongest relationship with the Trump vote.
Of course, she doesn't want to give too much information away for free, so she runs the analysis for just a couple of variables for now. One, naturally, has to be blue-collar workers. GWR calculates a coefficient for each county indicating the relative strength of the relationship between the explanatory and dependent variables (in this case, the percentage of blue-collar workers in a county and the percentage of the vote that Trump got). The sign of the coefficient indicates whether the relationship is positive or negative. A coefficient of 3.0, for example, means that a 1 percent increase in the percentage of blue-collar workers in that county resulted in a 3 percent increase in the Trump vote.

Her map of coefficients shows that the relationship does indeed vary substantially across the country. While looking at the map, it's apparent to the analyst that one thing she will have to make clear to clients is that the areas that are dark gray are not necessarily the areas where there are relatively more blue-collar workers. Rather, those areas are where the relationship between the percentage of blue-collar workers and the Trump vote is strongest.
To make the point, she decides she will also present the corresponding map showing which counties have a high percentage of blue-collar workers.

Comparing the two maps, she sees that in a large portion of the Northeast, for example, the relationship is strong, but many counties have a low percentage of blue-collar workers. There is a notable exception, however—the counties in central Pennsylvania and West Virginia have high percentages of these workers. A message that is geared to blue-collar workers and is targeted to this area could have an outsized impact on the vote in these states.
Though she's a data analyst and not a messaging expert, she thinks her marketing pitch to clients will be more effective if she can identify some potential campaign messages for this demographic, just as examples. No doubt, candidates of either party will want to focus heavily on a message of "Jobs! Jobs! Jobs!" (For Republicans, it will be a matter of building on Trump's popularity during the election; for Democrats, an attempt to win back some voters.) She can also point out the specific issues a candidate would want to run on (or away from), such as increased infrastructure spending (creating new blue-collar jobs) or renegotiating international trade agreements (to create a more level playing field for U.S. workers).
Now she runs GWR for the percentage of the population with a college degree.

The percent college graduates variable has a predominantly negative relationship with the Trump vote. In counties where there is a high percentage of people with college degrees, the percentage of the vote for Trump was low. That's true for much of the West, the Northeast, portions of the Midwest, and Florida. These are regions where focusing on issues important to college-educated voters could pay off. Perhaps a message based on providing affordable education and relief for student debt might motivate these voters to turn out.
Interestingly, there are some counties where the percentage of the population with a college degree has a positive relationship with the Trump vote (counties in light gray above). But these are mainly in areas that went heavily for Trump in all cases, such as the Great Plains and the Deep South.
Zeroing in
By looking at one variable at a time, these national-level coefficient maps provide opportunities for broad-level messaging, and this is helpful. Their effectiveness in terms of targeting messages to specific areas is limited, however. To develop more actionable results, the analyst will need to model vote outcomes using a complete set of explanatory variables. Based on what she saw with the GWR coefficients, though, she knows that the key variables are not the same everywhere across the country. So, she will need to focus on small regions of the country. The smaller the study area, the better the chances of finding the complete set of key explanatory variables and a properly specified regression model.
Finding properly specified regression models for specific states and regions is much more powerful than finding broad correlations. With a properly specified model, she will understand which variables are important in each area. That will allow her clients to be as effective as possible in designing messaging strategies.
Previously, the analyst used Exploratory Regression to identify broad correlations nationally. She will use it again, but this time to look for a properly specified model that will explain the percentage of the Trump vote in specific areas of the country.
She has already collected about 30 basic socioeconomic variables. However, she will not find a properly specified model if she is missing any key explanatory variables. Undoubtedly there are other characteristics of the electorate that help explain Trump's success. After some serious thought, she starts to come up with some ideas.
With ArcGIS, she has access to Tapestry LifeMode groups. Tapestry divides the population into segments that contain similar households based on a collection of variables—income level, education, consumer preferences, preferred pastimes, and so on. While they will cover some of the same ground as the demographic variables she already included, the LifeMode segments might pick up factors that she's missed. They will also provide the opportunity for more targeted messaging than will the individual demographic variables. Most important, including these LifeMode categories in the analysis may give the firm an advantage over the competition.
She decides to include all 67 segments. Again, she has to calculate percentages—this time it's the percentage of households in each LifeMode category in each county.

At this point the analyst has almost 100 variables for her analysis. But she needs to try to make sure she has all the key variables. Did she miss anything? Scanning back through the articles on the election, she sees a number of references to the dichotomy between the urban elites and the more rural heartland voters. It's true that the LifeMode segments capture these characteristics of the electorate, to some extent, but she thinks perhaps she can include a more direct measure of this phenomenon. So the analyst also includes the Tapestry Urbanization groups, which classify the LifeMode segments into six categories, ranging from urban centers to rural areas.
In addition, she calculates the distance from each county to a major city (such as Los Angeles, Chicago, or New York). It will be interesting to see, she thinks, if there is a strong relationship between the vote for Trump and the distance a county lies from one of these major metropolitan areas.
This gets her thinking about other spatial variables. Attitudes toward immigration were apparently one important indicator of the Trump vote, according to some of the exit polling. Trump played to this with his call to build a wall along the Mexican border. Perhaps how far a county lies from the border was a significant variable in the vote for Trump. The analyst uses ArcGIS to calculate the distances and includes this variable in her counties layer.
She has completed her search for explanatory variables and is confident she must have included all the key ones. Now it's time to choose some states or regions to focus on.
To identify study areas for this demonstration analysis, she decides to look at clusters of battleground counties, starting broadly with those where the difference between Trump and Clinton was less than 20 percentage points (that is, where a candidate won with less than 60% of the vote). She figures these counties will hold particular interest for potential clients. An analysis by FiveThirtyEight showed that in special elections for the first half of 2017, the average swing from 2016 was about 15 points (toward the Democrats, as it happens) but was even more than that in several individual elections. So, using a twenty-point spread seems reasonable to identify counties that have a better chance of electing a candidate from either party.

She notices there is a distinct cluster of battleground counties in Colorado, extending south into New Mexico. This makes some sense—Colorado of late has been considered a swing state in national elections, and New Mexico, while generally a blue state, is always a tighter race than the Democrats would like. This seems like a good region to start with.
Even though not every county in Colorado and New Mexico is a battleground county, for the local-level analysis she will include them all—having a complete statewide analysis will be useful for statewide offices (Governor, U.S. Senate), district-level campaigns (U.S. House of Representatives, state legislative races), and possibly even local and countywide campaigns.
To make things more interesting, she includes Arizona. While voting reliably Republican in statewide and national elections, Arizona always seems on the verge of becoming a swing state, given the growing Hispanic population. (In fact, Hillary Clinton advertised and ca
mpaigned in Arizona late in the 2016 election, but ended up losing by 3.5 percent. Still, that was an improvement for the Democrats over 2012, when President Obama lost the state by 9 percent.)
From the layer of counties that cover the entire continental United States, the analyst selects the counties within the three states. With Arizona included, the analyst now has a total of 112 counties for the analysis.

May the best model win
The Exploratory Regression tool builds Ordinary Least Squares Regression (OLS) models up to a specified number of variables, using every possible combination of the candidate explanatory variables provided. It looks for properly specified models. A properly specified (passing) model meets the requirements of the OLS method, which basically means you can trust the results.
The analyst starts small, looking for passing models that include three variables. No passing models are found. She excludes explanatory variables that are rarely significant or are redundant and tries to find a model using combinations of four explanatory variables. She finds nothing. When she runs Exploratory Regression looking for models with five explanatory variables, she still isn't getting any passing models.
The analyst decides she needs to rethink her analysis. Most likely, she is still missing some key variables. But which ones? She has included just about every relevant variable she could think of. So, she heads back to the Internet to see if there are any articles or studies she missed that might offer a hint, and she discovers an article written just after the election that includes a small clue. In this analysis of county-level data for the entire country, the author found that while the Hispanic population in a county was associated with a higher percentage of the vote for Clinton, the increase in Hispanic population in a county was associated with a higher percentage for Trump. The author of the article conjectured that there might be white identity politics at play. That is, there was a sort of backlash effect where in counties that had a strong influx of Hispanics, Trump's anti-immigration rhetoric played well. The analyst suspects this might especially apply in her Southwestern study area.
The analyst adds a variable to capture the increase in the percentage of the population that is Hispanic between 2010 and 2016.
Before turning back to Exploratory Regression, she thinks she should take a look at a map of the region to see if there are any other variables she might be missing. Right away, she notices the large number of Indian reservations in the region.

While she initially included variables for the black, white, Asian, and Hispanic populations, she did not include the Native American population—it is a small portion of the population in most states. But that's not the case in Arizona and New Mexico, or in southern Colorado. This could be another important explanatory variable.
Crossing her fingers, she tries Exploratory Regression again, specifying five variables. She finally has success—a passing model, and it includes the variable for change in Hispanic population (although not the Native American population variable). The adjusted R2 value for the model is just over 0.82, indicating the passing model is telling about 82 percent of the election result story. She will increase the number of variable combinations to see if it uncovers an even better model.
With six variables, she gets three passing models, and one of them includes the variable for the Native American population, so this looks like a key variable as well. The top two six-variable models have an R2 value close to 84 percent, a little higher than the passing five-variable model (they tell 84 percent of the story).
The analyst could continue to create models with an increasing number of explanatory variables—seven, or even eight—to see if they generate higher R2 values.
However, she recalls reading somewhere in her research for the project that with too many explanatory variables a model can become overly complex. The danger is that the model will begin describing random error in the data rather than the relationships between variables. This is known as overfitting a model.
The analyst has to make a decision. Should she keep looking for higher R2 values, and risk overfitting (which will make the R2 values suspect in any case), or move forward with the four passing models she has generated so far?
She notices that several variables are the same in the passing models—that gives her confidence that she is homing in on the key variables. Since the analyst's goal for this demonstration project is simply to identify a couple of key explanatory variables she can use to develop some sample campaign messaging, she decides to move forward with the models she has.
Next she will determine which variables occur most frequently in the models she generated, and then, of those, which two have the largest coefficients and thus the strongest relationship with the Trump vote. She will focus on these for her sample campaign messaging.
Passing the test
The analyst creates a spreadsheet for the passing models, showing the explanatory variables in each.

Four variables occur in all four models. These are clearly frequently occurring. She decides she will also look at any variables that occur in over half the models. There is only one additional variable: % Republican Party.
Since all of the frequently occurring variables are percentages, she can compare the coefficients of the variables to determine which have the strongest relationship with the dependent variable (percent Trump vote). This will help her narrow down the number of variables to focus on.
To get the coefficient values, she runs Ordinary Least Squares (OLS) using one of the models. While Exploratory Regression runs OLS under the hood, it only reports the significance and direction (positive or negative) of the relationship; it doesn't report the coefficient values associated with each explanatory variable. The model she uses to get the coefficient values must include all five frequently occurring variables, while containing the fewest overall number of variables, and having the highest R2 value. Model 6A fits the requirements.
She creates a chart that orders the coefficients from the OLS output from largest to smallest. The largest coefficients (either negative or positive) have the strongest impact on the percent Trump vote.

The analyst notes that in this region, the strongest relationship is positive (1.77) and is associated with the change in Hispanic population—a 1 percent increase in the change in Hispanic population in a county between 2010 and 2016 is associated with a 1.77 percent increase in the Trump vote in that county. The relationship with the percentage of the population having a college degree is also quite strong—a 1 percent increase in this population is associated with a 1.02 percent decrease in the Trump vote (assuming all other explanatory variables are held constant).
Energizing the vote
The regional and state levels are where targeted messaging can be really effective. The analyst decides to once again try her hand at identifying some example campaign messages.
She first turns to the counties that have experienced a rapid increase in the Hispanic population (dark green in the map below). A Republican campaign might target these counties with a message around border security to motivate Trump voters who bought into his rhetoric ("Build the wall!") to turn out in the next election.

A Democratic campaign, by contrast, might have a more difficult time putting together a message that appeals to voters for whom this issue is important. Fostering an identity around diversity and emphasizing its benefits is an option, although one that's unlikely to convert many Trump voters in these counties. In any case, knowing where to avoid certain messages is also useful information.
Democrats might find more fertile ground in counties with a high number of people with a college degree. A message based on the issues she identified earlier—affordable education and student debt relief—could be effective. In addition, these voters generally have high incomes, so perhaps another message that would play well would be one that protects 401(k) accounts from cuts in contribution limits.

The analyst decides that her sample messaging for the Southwest region is at least somewhat plausible and will suffice for her demonstration purposes.
To be able to demonstrate to prospective clients that the explanatory variables likely vary from one region to the next, she decides to develop some models for a few other parts of the country.
She takes another look at her map of battleground counties. There is a cluster in the Rust Belt, around the Great Lakes. As was painfully clear on election night, some of these states were extremely close and likely decided the election. For sure she'll want to look at this area.
The whole eastern seaboard also consists of battleground counties. She doesn't need to look at the entire region, and likely wouldn't be able to find a properly specified model for such a large area in any case. But the mid-Atlantic states of Virginia and North Carolina have some interesting, and changing, demographic patterns and trends—Virginia voted Republican in the 2000 and 2004 presidential elections, but Democratic since. In North Carolina, George W. Bush won big in 2000 and 2004, but Obama won in 2008 and barely lost in 2012. Trump won in 2016, but not by as much as Bush. It would be interesting to create a model for one of these states.
Virginia is for voters
Since she is more familiar with Virginia (having done an internship in Washington, D.C.), she decides to focus on that state for this demonstration analysis.

The analyst goes through a similar process to the one she used for the Arizona, Colorado, and New Mexico region. As it turns out, she is able to generate one passing model with six variables and five with seven variables. She breathes a huge sigh of relief that the method can be replicated—maybe she really is onto something.
After creating a spreadsheet of the variables that appear in the passing models, she discovers that the results are clear-cut. Six of the variables appear in all the models. She is confident that these are the most important factors for the 2016 vote in Virginia. And as she expected, most of the variables are different than the key variables for the Arizona, Colorado, and New Mexico region (percentage identifying White being the one exception). So that confirms that there are distinct regional differences in the vote.
To check the strength of the correlations, the analyst runs OLS with the six-variable model (it contains all six frequently occurring variables while having the fewest number of variables overall—the other models all had an additional variable). To keep her pitch to clients concise, she will again focus on the two variables with the strongest correlations (although she will also point out that two of the Tapestry LifeMode variables were among the six key variables).

As it turns out, the variables with the strongest relationship are both negatively correlated with the Trump vote, with the strongest being the percent of the population in each county that voted within the past twelve months—that is, engaged and reliable voters.

The analyst is a bit perplexed by this relationship. This may be one for political scientists to sort out. As for the practical implications for campaigns, the strategy might not involve a specific policy issue. Rather, in counties with a high percentage of these voters, Democrats might want to tie their opponent to Trump as closely as possible to drive a high vote turnout.
The second strongest relationship is with the percentage of people in each county who identify as Asian. That reinforces her earlier finding that there was a strong correlation nationwide between the percent Asian population and the vote for Clinton. Looking at a map of the percent Asian population in Virginia, she sees that the values range from a low of less than 1 percent of the population to a high of almost 20 percent. There are a number of counties where the Asian population is over 10 percent. For example, in one county alone (Fairfax), the Asian population is just over 220,000. If this population is registered to vote at the same rate as the state as a whole (65 percent of the population is registered), there would be over 140,000 potential voters of Asian extraction in the county. In the 2013 gubernatorial race, Governor Terry McAuliffe won by just 56,000 votes statewide.

But what is a specific message for these voters? Doing a little research online, the analyst finds that immigration from Asia has grown rapidly in recent years, for the United States as a whole.

Asian Americans might have family members who wish to immigrate, or at least be able to travel to the United States. Perhaps a Democratic message based on more liberal travel and immigration policies will sway at least some of these voters, especially in light of the Trump Administration's plan to cut legal immigration and change the program to one based on merit over family ties.
A Republican campaign, by contrast, might target this demographic group using a message based on rolling back affirmative action, which some claim discriminates against Asian students.
Rust Belt swing
For the final phase of the project, the analyst focuses on the cluster of battleground states in the Rust Belt. During the campaign, there was a lot of coverage of this region. And indeed, from her data she sees that the two states Trump won by the fewest votes are Michigan and Wisconsin—his margin was just over 10,000 votes and 22,000 votes, respectively. If these two states had gone the other way, along with Pennsylvania (another tight race), Hillary Clinton would be in the White House. There is bound to be an inordinate amount of interest in these two states in 2018 and 2020 on the part of campaigns and the media.
From her research she knows that the two states were among the six that voted for Obama in 2012 but Trump in 2016 (the others being Pennsylvania, Florida, Iowa, and Ohio). The analyst is sure the future campaigns will want to know which factors are correlated with voters switching from Obama to Trump. She decides that for this analysis, instead of finding the variables that are correlated with the 2016 GOP vote in each county, she will instead find the correlation with the percentage change in the GOP vote from the 2012 election to the 2016 election. Republican campaigns will want to try to keep voters that moved toward the GOP, while the Democrats will want to try to flip them back into their column.

Furthermore, in the analyses she's seen, the two states are often lumped together. It will be really interesting, she thinks, to see if the key variables for the two adjacent states are similar. She'll identify the key variables for each state and map the corresponding populations, and then see if there are broader themes for the region that can be used as the basis for campaign messaging.
After giving it some additional thought, the analyst decides the variables to focus on in this case are the ones that are positively correlated with the highest increase in the GOP vote between 2012 and 2016, at least for this demonstration analysis. What she wants to find out—and what campaigns will want to know—is which factors led to a county moving strongly from Obama to Trump. (A case could be made that Democratic campaigns might want to know which factors are correlated with a small increase, or even a decrease, in the GOP vote—focusing on those factors could help mitigate the slippage in the Democratic vote. But she'll put that aside for now).
Applying her methodology, she sets about finding passing models for Michigan. She generates six passing models using six variables, the best with an R2 of 81 percent. She runs Exploratory Regression to generate passing models using seven variables, and gets 48 of them. Well, she doesn't need all of them to find the frequently occurring variables—she can see just by glancing at the report file that the same variables keep showing up in the top models. To narrow down the number of models for her spreadsheet, she decides to use only the seven-variable models that score better than the best six-variable model. Of course, that means those with an R2 value higher than 81 percent.
But she remembers that Exploratory Regression returns another diagnostic that can help her compare different models. The AICc value (Akaike's Information Criterion) considers model complexity and fit. The model with the smallest AICc value is doing the best job explaining the dependent variable. From the documentation, she knows that models with AICc values that differ by less than 3 essentially do an equally good job of explaining the dependent variable.
The best six-variable model has an AICc value of -404.8. So she includes any of the seven-variable models that are lower than this by more than 3 (that is, have an AICc value of -407.8 or lower). There are eight of these models.
After constructing her spreadsheet, she sees that in fact the best six-variable model contains the six most frequently occurring explanatory variables. She runs OLS with this model to get the coefficients.

The two variables with the strongest relationship are both positively correlated with the increase in the Trump vote, so these are the two she will focus on.
The counties with a relatively high number of people having less than a high school education appear to be clustered in the north central part of the state.

The swing counties also have a high percentage of households that speak only English—that is, there are likely relatively fewer immigrants in these counties. The counties with a high number of these households are found mainly in the central part of the state, and in the Upper Peninsula. The range of values for all the counties is quite narrow—most counties have between 58 percent and 72 percent of households speaking only English, so targeting these voters specifically—by county, anyway—might not be that easy.

Moving on to Wisconsin, the analyst gets passing models using two and three variables. While there are three passing models using two variables, there are 30 more three-variable models that score better than the best two-variable model.
Finding the most frequently occurring variables among the models is not as straightforward as with the previous cases. There is only one variable that occurs in more than half the models—average household income—and it is negatively correlated with the Trump vote. Scanning through her spreadsheet, she sees that there are two positively correlated variables that do occur in multiple models—the percentage of semirural households (occurring in eight models) and the percentage of blue-collar workers (occurring in five models). The analyst decides that that's a strong enough case to make for focusing on these two variables. While it deviates a bit from her methodology for finding the most frequently occurring variables, she figures that sometimes in this business you have to be a little flexible. Counties with a high percentage of semirural households are mainly found in the western half of the state, and in the northeast.

There is some overlap between counties with a high percentage of semirural households and those with a high percentage of blue-collar workers—especially in the northern half of the state—but also clusters of blue-collar workers in the south.

The analyst now has solid results for the two states, demonstrating that her methodology can be applied to different dependent variables, as well as different locations. And the results are consistent with much of the existing election analysis of these and other Rust Belt states. That's good—it will give her analysis some credibility. The last step is to develop messaging around the results.
Stepping back to look at the big picture, the analyst thinks that perhaps all of these factors suggest a cultural phenomenon at play—mainly voters lower on the economic ladder, often blue collar or with little education and probably living in rural or semirural areas, who were hopeful about Obama, but subsequently came to feel their concerns and needs have been ignored by the coastal elites, were drawn to Trump's populist message. For both states, Democrats clearly need to do a better job of appealing to these voters and winning them back. Developing policies and messaging around issues such as funding for infrastructure projects, economic development, job training, and access to health care would be a good place to start.
Spreading the word
With her three cases—the Southwest, Virginia, and the Rust Belt—the analyst now has three good examples of how her methodology can be applied to create targeted messaging to different parts of a state or region. Once the 2018 election is over she will review the results of her predictions, nationally and regionally, and modify her analysis if necessary.
Her analysis is complete for now, and she came in only slightly over budget. The next step is to let candidates and campaigns know about these new analytic services the firm offers. A story map that presents the ideas behind the analyses, without giving away all the results, will hopefully generate some press and help get the word out.
Spending on campaigns grows dramatically each election cycle. The firm will be well positioned to get its portion of the profits next time. At least that's how the firm's management views things. As for the analyst, she hopes that her methodology will contribute to the art and science of election analysis, and just maybe, help candidates and elected officials better understand and address the needs of their constituents.
Always dreamed of being a campaign consultant? You can try out the analyst's methods using her data and workflow. Or, apply the analyst's approach using your own data. The approach can also be used in any application where you want to find the relationship between two or more variables—marketing, public health, finance, and many others.