Avant d'utiliser la méthode Krigeage de fenêtre en mouvement, vous devez créer une couche géostatistique à partir d'une méthode de krigeage autre que le co-krigeage et le krigeage bayésien empirique.
Vous pouvez ajuster les paramètres de krigeage ou conserver les valeurs par défaut initiales automatiquement déterminées par la méthode de krigeage. La logique du krigeage de fenêtre en mouvement consiste à recalculer les paramètres de plage, de pépite et de semi-variogramme de seuil partiel en fonction d'un voisinage plus restreint.
Lorsque les données ne sont pas stationnaires, vous pouvez estimer un semi-variogramme hétérogène. Autrement dit, utilisez une fenêtre en mouvement centrée sur l'emplacement à prévoir et créez un semi-variogramme pour chaque voisinage local.
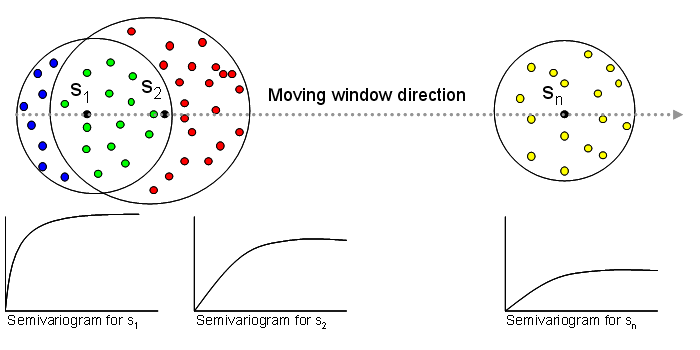
La prévision à chaque point de la zone d'étude peut être cartographiée séquentiellement au fur et à mesure que la fenêtre se déplace dans la zone d'étude (figure 1). Dans cet exemple, les données sont isotropes ou invariantes lorsqu'elles sont soumises à des rotations. Pour cartographier intégralement chaque emplacement de la zone d'étude, des semi-variogrammes sont calculés pour chaque emplacement à prévoir. Dans chaque voisinage, il est supposé que les données sont stationnaires localement pour que les hypothèses de l'algorithme de krigeage soient respectées.
Alors que la fenêtre se déplace dans la zone d'étude, de nouveaux paramètres de semi-variogrammes sont calculés à l'aide de points voisins. Pour l'emplacement s1, les points bleus et verts sont spatialement corrélés ou dans les limites de distance, comme l'indique le rayon du cercle centré à cet emplacement. Pour l'emplacement s2, les points verts et rouges sont spatialement corrélés et pour l'emplacement sn, les points jaunes sont spatialement corrélés. Cette méthode vous permet de voir comment la structure spatiale des données change dans la zone d'étude. Si le semi-variogramme ne change pas beaucoup d'une fenêtre à une autre, cela indique que les données sont presque stationnaires et que vous devez utiliser des modèles de krigeage stationnaire. Toutefois, si le semi-variogramme change considérablement d'une fenêtre en mouvement à une autre, cela indique que les données ne sont pas stationnaires et qu'il ne faut pas utiliser de modèles de krigeage stationnaire.