Die Detaillierungsebene (von Features/Phänomenen) eines Rasters hängt häufig von der Zellengröße (Pixel) bzw. der räumlichen Auflösung des Rasters ab. Die Zelle sollte klein genug sein, um das erforderliche Detail zu erfassen, aber auch groß genug, damit die Speicherung im Computer und die Analysen effizient durchgeführt werden können. Mehr Features, kleinere Features oder eine größere Genauigkeit bei den Ausdehnungen der Features können mit einem Raster mit kleinerer Zellengröße dargestellt werden. Mehr ist jedoch nicht immer besser. Eine kleinere Zellengröße führt zu größeren Raster-Datasets bei der Darstellung einer Oberfläche. Daraus ergibt sich ein größerer Speicherplatzbedarf, der wiederum häufig zu längeren Verarbeitungszeiten führt.
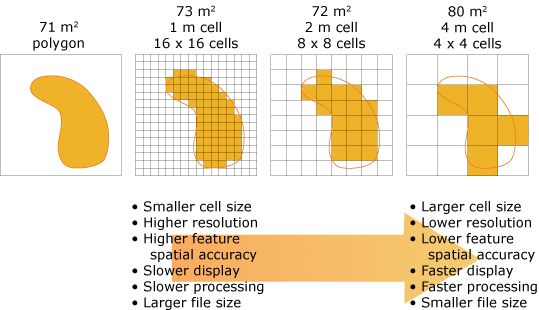
Das Auswählen der geeigneten Zellengröße ist nicht immer einfach. Sie müssen zwischen der für eine Anwendung benötigten räumlichen Auflösung und praktischen Anforderungen im Hinblick auf Anzeigegeschwindigkeit, Verarbeitungszeit und Speicherplatz abwägen. In einem GIS sind die Ergebnisse im Wesentlichen nur so genau wie das ungenaueste Dataset. Wenn Sie ein klassifiziertes Dataset verwenden, das aus Landsat-Bildern mit einer Auflösung von 30 Metern abgeleitet wurde, ist das Erstellen eines digitalen Höhenmodells (DHM) oder anderer Hilfsdaten mit einer höheren Auflösung von z. B. 10 Metern möglicherweise nicht erforderlich. Je gleichmäßiger eine Fläche bei wichtigen Variablen wie Topographie und Landnutzung ist, desto größer kann die Zelle sein, ohne dass die Genauigkeit beeinflusst wird.
Das Bestimmen einer geeigneten Zellengröße ist während der Planung einer GIS-Anwendung genauso wichtig wie das Bestimmen erforderlichen Datasets. Ein Raster-Dataset kann stets für größere Zellen neu berechnet werden. Allerdings erhalten Sie beim Resampling eines Rasters für eine kleinere Zellengröße keine höhere Detaillierungsebene Je nach geplanter Verwendung der Daten kann es lohnenswert sein, eine Kopie der Daten mit der kleinsten und genauesten Zellengröße zu speichern, während ein Resampling der Daten für die größte und ungenaueste Zellengröße durchgeführt wird. Dies kann die Verarbeitungsgeschwindigkeit der Analyse erhöhen.
Berücksichtigen Sie beim Angeben der Zellengröße folgende Faktoren:
- Räumliche Auflösung der Eingabe-Daten.
- Anwendung und die Analyse, die durchgeführt werden soll
- Größe der resultierenden Datenbank im Vergleich zur Festplattenkapazität
- Gewünschte Antwortzeit
Auflösungstypen
Für Bild-Raster-Daten werden vier Auflösungstypen verwendet: räumliche Auflösung, Spektralauflösung, zeitliche Auflösung und radiometrische Auflösung.
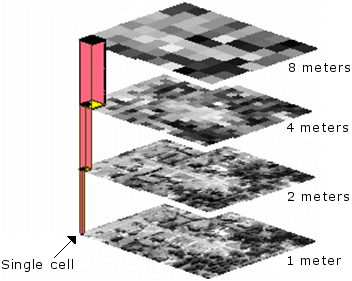
In einem GIS befassen Sie sich meist mit der räumlichen Auflösung eines Raster-Datasets, insbesondere beim Anzeigen und Vergleichen von Raster-Daten mit anderen Datentypen, beispielsweise Vektoren. In diesem Fall bezieht sich "Auflösung" auf die Zellengröße (die Bodenfläche, die von einer einzelnen Zelle dargestellt wird). Aus einer höheren räumlichen Auflösung ergibt sich eine größere Zellenanzahl pro Flächeneinheit. Die Grafik links bietet also eine höhere räumliche Auflösung als die Grafik rechts.
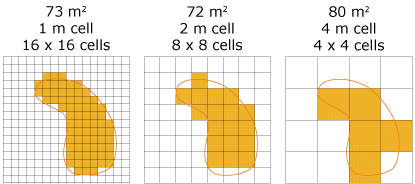
Die Spektralauflösung bezeichnet die Fähigkeit eines Sensors, Wellenlängenintervalle im elektromagnetischen Spektrum zu unterscheiden. Je höher die Spektralauflösung, desto schmaler ist der Wellenlängenbereich für ein bestimmtes Band. Beispielsweise werden für eine Luftaufnahme (ein Luftbild) mit Einzelband-Graustufen Wellenlängendaten aufgezeichnet, die weit über den sichtbaren Bereich des elektromagnetischen Spektrums hinausreichen. Daher liegt eine niedrige Spektralauflösung vor. Für ein Farbbild (mit drei Bändern) werden im Grunde genommen Wellenlängendaten aus drei kleineren Abschnitten des sichtbaren Teils des elektromagnetischen Spektrums erfasst: Rot, Blau und Grün. Daher verfügt jedes Band eines Farbbildes über eine höhere Spektralauflösung als das Einzelband eines Graustufenbildes. Hochentwickelte multispektrale und spektrumsübergreifende Sensoren erfassen Daten aus mehreren hundert schmalen Bändern aus verschiedenen Teilen des elektromagnetischen Spektrums. Dies führt zu Daten mit sehr hoher Spektralauflösung.
Zeitliche Auflösung bezieht sich auf die Frequenz, mit der Bilder desselben Ortes auf der Erdoberfläche erfasst werden. Eine andere Bezeichnung dafür lautet "Wiederholrate", ein häufig verwendeter Begriff in Bezug auf Satellitensensoren. Daher verfügt ein Sensor, der einmal pro Woche Daten erfasst, über eine höhere zeitliche Auflösung als ein Sensor, der einmal pro Monat Daten erfasst.
Die radiometrische Auflösung bezeichnet die Fähigkeit eines Sensors, Objekte im gleichen Abschnitt des elektromagnetischen Spektrums zu unterscheiden. Dies ist gleichbedeutend mit der Anzahl möglicher Datenwerte pro Band. Beispielsweise enthält ein Landsat-Band in der Regel 8-Bit-Daten, ein IKONOS-Band jedoch in der Regel 11-Bit-Daten. Daher weisen die IKONOS-Daten eine höhere radiometrische Auflösung auf.
Räumliche Auflösung und Maßstab
Die räumliche Auflösung bezieht sich auf die Bemaßung der Zellengröße für eine Bodenfläche. Wenn also die von einer Zelle abgedeckte Fläche 5 x 5 Meter groß ist, beträgt die Auflösung 5 Meter. Je höher die Auflösung eines Rasters ist, desto kleiner ist die Zellengröße und desto detaillierter ist folglich die Darstellung. Für den Maßstab gilt das Gegenteil. Der Detaillierungsgrad hängt vom Maßstab ab. Beispielsweise sind auf einer Orthofotografie im Maßstab 1:2000 mehr Details zu erkennen (erscheint vergrößert) als auf einer im Maßstab 1:24000 (erscheint verkleinert). Wenn jedoch dieses Orthofoto eine Zellengröße von 5 Metern aufweist, bleibt die Auflösung maßstabsunabhängig gleich, da sich die physische Zellengröße (die Bodenfläche, die von einer einzelnen Zelle dargestellt wird) nicht ändert.
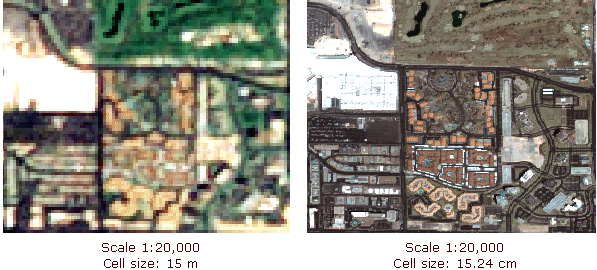
In den folgenden Abbildungen ist der Maßstab des linken Bildes (1:50000) kleiner als der des rechten Bildes (1:2500). Die räumliche Auflösung (Zellengröße) der Daten ist jedoch identisch.

In den folgenden Abbildungen ist die räumliche Auflösung der Daten im linken Bild geringer als die der Daten im rechten Bild. Folglich ist die Zellengröße der Daten im linken Bild größer als die der Daten im rechten Bild. Der Anzeigemaßstab ist jedoch identisch.