Die Form und Größe der Oberfläche eines geographischen Koordinatensystems werden von einer Kugel oder einem Sphäroid definiert. Zwar wird die Erde am besten durch einen Sphäroid dargestellt wird, allerdings wird sie zur Vereinfachung mathematischer Berechnungen manchmal auch als Kugel dargestellt. Für Karten mit kleinem Maßstab (kleiner als 1:5.000.000) kann die Erde als Kugel dargestellt werden. Bei diesem Maßstab ist der Unterschied zwischen einer Kugel und einem Sphäroid auf einer Karte nicht mehr erkennbar. Um für Karten größeren Maßstabs (1:1.000.000 oder größer) die Genauigkeit zu erhalten, ist jedoch ein Sphäroid erforderlich, um die Form der Erde darzustellen. Bei beiden Maßstäben hängt die Entscheidung für eine Kugel oder einen Sphäroid vom Zweck der Karte und der Genauigkeit der Daten ab.
Definition eines Sphäroids
Eine Kugel basiert auf einem Kreis, während ein Sphäroid (oder Ellipsoid) auf einer Ellipse basiert.
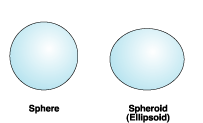
Die Form einer Ellipse wird von zwei Radien definiert. Der längere Radius wird als große Halbachse bezeichnet, der kürzere Radius wird als kleine Halbachse bezeichnet.
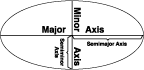
Wird die Ellipse nun um die Halbachsen gedreht, entsteht ein Sphäroid. Ein Sphäroid wird auch als abgeplattetes Rotationsellipsoid bezeichnet. Die folgende Grafik zeigt die große und die kleine Halbachse eines Sphäroids.
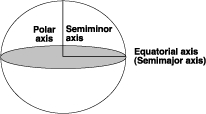
Ein Sphäroid wird entweder durch die große Halbachse a und die kleine Hauptachse b oder durch a und die Abflachung definiert. Die Abflachung ist die Längendifferenz zwischen den beiden Achsen und wird entweder als Bruchzahl oder als Dezimalzahl angegeben. Die Abflachung f wird wie folgt abgeleitet:
f = (a - b) / aDie Abflachung ist ein kleiner Wert, sodass stattdessen meist die Menge 1/f verwendet wird. Dies sind die Sphäroidparameter für das World Geodetic System von 1984 (WGS 1984 oder WGS84):
a = 6378137.0 meters
b = 6356752.31424 meters
1/f = 298.257223563Die Abflachung liegt zwischen 0 und 1. Der Abflachungswert 0 bedeutet, dass die zwei Achsen gleich sind und entsprechend eine Kugel darstellen. Die Abflachung der Erde beträgt ungefähr 0,003353. Eine weitere Menge, die ähnlich wie die Abflachung die Form eines Sphäroids beschreibt, ist das Quadrat der Exzentrizität e2. Dieser Wert wird folgendermaßen dargestellt:
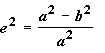
Definition von verschiedenen Sphäroiden für eine genaue Zuordnung
Die Erde ist bereits mehrfach vermessen worden, um ihre verschiedenen Oberflächen und deren individuellen Unregelmäßigkeiten besser nachzuvollziehen. Die Vermessungen haben viele verschiedene Sphäroide ergeben, die alle die Erde darstellen. Im Allgemeinen wird ein Sphäroid ausgewählt, der ein Land oder eine bestimmte Fläche am besten repräsentiert. Das für eine Region am besten geeignete Sphäroid ist für eine andere Region nicht zwangsläufig ebenso geeignet. Bis vor kurzem wurde für nordamerikanische Daten ein Sphäroid verwendet, der 1866 von Clarke festgelegt wurde. Die große Halbachse dieses Sphäroids beträgt 6.378.206,4 Meter; die kleine Halbachse beträgt 6.356.583,8 Meter.
Aufgrund von Gravitations- und Oberflächenvariationen ist die Erde weder eine perfekte Kugel noch ein perfektes Sphäroid. Dank der Satellitentechnologie konnten mehrere elliptische Abweichungen aufgedeckt werden; der Südpol ist z. B. näher am Äquator als der Nordpol. Aus Satellitendaten hervorgegangene Sphäroide ersetzen nach und nach die älteren, am Boden vermessenen Sphäroide. Das neue Standardsphäroid für Nordamerika ist z. B. das Geodetic Reference System von 1980 (GRS 1980), dessen Radien 6.378.137,0 Meter und 6.356.752,31414 Meter betragen. Die Sphäroidparameter für GRS 1980 wurden 1979 von der Internationalen Union für Geodäsie und Geophysik festgelegt.
Da eine Änderung des Koordinatensystems eines Sphäroids eine Änderung aller Feature-Koordinatenwerte mit sich zieht, haben viele Organisationen bisher vermieden, die neueren (und genaueren) Sphäroide zu verwenden.